Tenttiin 12.4.2019 perustuva itseopiskelusivu
Tämän veppisivun avulla voit harjoitella kurssin TIEP1020 Diskreetit rakenteet tenttejä varten. Voit vastata 12.4.2019 pidetyn tentin kysymyksiin ja saada tietää onko vastauksesi oikein. Sivulla kerrotaan miksi oikea vastaus on sellainen kuin on ja annetaan linkkejä muille sivuille, joilla voi harjoitella kysymyksen käsittelemää asiaa.
Todellinen tentti oli paperilomake, jossa vastattiin annettuun tyhjään tilaan. Siinä ei saanut olla kirjoja, laskinta tms. Jokainen tehtävä oli tasan 6 pisteen arvoinen. Pisteet jakautuivat tasan alakohtiin (a), (b) jne., paitsi missä sanottiin toisin. Pisteytys ei ollut ”kaikki tai ei mitään” -periaatteella, vaan oikeansuuntainen vastaus tuotti osan pisteistä, tehtävästä riippuen jopa neljäsosapisteittäin.
Eri tenteissä on tietenkin eri kysymykset. Aihepiirit ovat kuitenkin paljolti samoja. Tämän tentin vastausten ulkoa opettelu ei todennäköisesti auta paljoa tulevissa tenteissä. Vastausten takana olevien periaatteiden opettelu niin, että osaa soveltaa niitä erilaisissa tilanteissa, auttaa todennäköisesti hyvin paljon. Alla olevien selitysten ja esimerkkien tavoitteena on auttaa ymmärtämään ne.
Lyhyt ohje symboleiden syöttämiseksi vastauskenttiin löytyy täältä. Vastausnappi ”oikealle” tuottaa palautteen oikealla olevaan laatikkoon. Yleensä on kätevintä ensin klikata sitä. Vastausnappi ”uuteen” tuottaa palautteen uuteen välilehteen tai uuteen ikkunaan riippuen selaimesi asetuksista. Sitä kannattaa käyttää, jos ”oikealle”-napin tuottama palaute ei mahdu laatikkoon.
Ruskeissa alueissa on piilossa tekstejä, jotka tulevat näkyviin, kun siirrät kursorin niitten päälle. Kokeile tästä!Toimii! Joidenkin piilotekstien sisällä on sininen alueTämäkin toimii!, jossa on piilossa lisää tekstiä. Kokeile sekin! (Joissakin iPhoneissa tämä ei toimi.)
1. (a) Piirrä lausekkeen b + 1 ⋅ a + 0 lausekepuu.
Yleinen väärä vastaus selityksineen
Tämä puu on väärin, koska kertolasku sitoo voimakkaammin kuin yhteenlasku,
mutta tämä on piirretty ikään kuin yhteenlasku sitoisi voimakkaammin.
Tämä olisi oikein lausekkeelle (b + 1) ⋅ (a + 0).
Eräs väärä vastaus selityksineen
Tämä puu on väärin, koska osuudet 1 ⋅ a ja b ovat vaihtaneet
paikkaa.
Sillä ei ole merkitystä, että b + 1 ⋅ a ja 1 ⋅ a + b
tuottavat matematiikassa saman tuloksen.
Lausekepuissa ei oteta huomioon mitä ilmaukset tarkoittavat, vaan ainoastaan
ilmausten rakenne.
Vielä yksi väärä vastaus selityksineen
Tämä puu on väärin, koska yhteenlasku on vasemmalle liitännäinen, mutta tämä
on piirretty ikään kuin yhteenlasku olisi oikealle liitännäinen.
Tämä olisi oikein lausekkeelle b + (1 ⋅ a + 0).
Kannattaa opiskella seuraavat asiat:
- Ym. selityksessä ja (b)-kohdan selityksessä mainitut periaatteet
- Matematiikan tuttujen operaattoreiden sitovuustasot
- Matematiikan tuttujen operaattoreiden liitännäisyyden suunnat
Aiheeseen liittyviä harjoituksia: linkki linkki
(b) Piirrä lausekkeen −x|n| − 2 − 3 lausekepuu.
Yleinen väärä vastaus selityksineen
Tämä puu on väärin, koska potenssilasku sitoo voimakkaammin kuin etumerkki,
mutta tämä on piirretty ikään kuin etumerkki sitoisi voimakkaammin.
Tämä olisi oikein lausekkeelle
(−x)|n| − 2 − 3.
Eräs väärä vastaus selityksineen
Tämä puu on väärin, koska siinä on osia, joita alkuperäisessä lausekkeessa ei
ole: ⋅ ja 1.
Tämä olisi oikein lausekkeelle (−1) ⋅ x|n| − 2 − 3.
Vaikka se tarkoittaa matemaattisesti samaa kuin alkuperäinen lauseke, on siitä
syntyvä puu kuitenkin eri puu, minkä näkee mm. siitä, että siinä on eri määrä
solmuja.
Lausekkeessa olevia sulkuja ei piirretä lausekepuuhun sellaisinaan, vaan niiden vaikutus ilmenee lausekepuun rakenteessa. Tästä on esimerkkejä edellä olleissa väärissä vastauksissa, katso ne nyt uudelleen jos asia ei jo ole sinulle selvä.
Potenssilaskulle ei ole matematiikassa omaa symbolia, koska se esitetään nostamalla eksponentti korkeammalle kuin muu teksti. Lausekepuun solmussa pitää kuitenkin jotenkin kertoa, että kyseessä on potenssilasku (eikä näkymätön kertolasku), joten solmuun kirjoitetaan ^. Vaakaviivan avulla esitetty jakolasku aiheuttaa saman ongelman. Se esitetään kirjoittamalla solmuun / tai ÷.
Tällaisia poikkeuksia lukuun ottamatta lausekepuun solmuissa esiintyvät samat symbolit yhtä monta kertaa kuin alkuperäisessä lausekkeessa.
S ::= ε | aSbSkuuluvat merkkijonot, joiden pituus on enintään 4.
Tehtävän kieliopin osuus ε tuottaa tyhjän merkkijonon.
Osuutta aSbS käytetään siten, että otetaan jokin kieleen kuuluva merkkijono, laitetaan se ensimmäisen S:n paikalle, otetaan jokin kieleen kuuluva merkkijono (saa olla sama tai eri merkkijono kuin edellinen), ja laitetaan se toisen S:n paikalle.
Käyttämällä molempien S:ien paikalla tyhjää merkkijonoa saadaan aεbε eli ab. Se on kirjoitettava vastaukseen muodossa ab eikä aεbε, koska ε edustaa tyhjää ja tarkoitus on, että ε kirjoitetaan näkyville vain silloin kun sen kirjoittamatta jättäminen saattaa aiheuttaa sekaannusta.
Alla oleva taulukko näyttää merkkijonojen muodostamista niin pitkälle, että kaikki enintään 4 merkin mittaiset merkkijonot ja kaksi pitempää on muodostettu.
ensimmäinen S toinen S välimuoto lopputulos ε ε aεbε ab ab ε aabbε aabb ε ab aεbab abab ab ab aabbab aabbab aabb ε aaabbbε aaabbb
Kirjoittakaa tenttipaperiin tyhjäksi merkkijonoksi ε eikä esimerkiksi ""! Näin siksi, että matematiikassa tyhjän merkkijonon symboli on ε. Tarkastusohjelma käyttää merkintää "" vain siksi, että ε on kovin hankala kirjoittaa näppäimistöltä (lisätietoja).
Aiheeseen liittyviä harjoituksia: linkki linkki
2. (a) Luettele luvun 18 tekijät.
Aiheeseen liittyviä harjoituksia: linkki
(b) Ilmoita seuraavien lukujen viimeinen numero.
| 32 | |
| 33 | |
| 35 | |
| 32019 |
Tässä tärkeitä osaamistavoitteita ovat:
- Yhteen-, vähennys- ja kertolaskun lopputuloksen viimeinen numero riippuu
vain yhteenlaskettavien tms. viimeisestä numerosta.
(Jakolaskulle ja potenssilaskun eksponentille tämä ei päde.)
Siksi lukuja 35 ja 32019 ei tarvitse laskea kokonaan, vaan riittää käyttää viimeistä numeroa. Koska 33 = 27, sen viimeinen numero on 7. Siksi luvun 34 viimeinen numero on sama kuin luvun 3 ⋅ 7 = 21 viimeinen numero eli 1. Samasta syystä luvun 35 viimeinen numero on sama kuin luvun 3 ⋅ 1 = 3 viimeinen numero eli 3.
Tämä on esimerkki yleisemmästä periaatteesta, jota kannattaa osata käyttää: luvut (n + m) mod M, (n − m) mod M ja (nm) mod M riippuvat vain luvuista n mod M ja m mod M.
- Kannattaa opetella hyödyntämään jaksollisuutta, koska sille on käyttöä
muuallakin kuin lukuteoriassa.
Luvun 34 viimeinen numero on sama kuin luvun 30
viimeinen numero.
Siksi kolmosen potenssien viimeinen numero toistaa jaksoa, jonka pituus on 4.
Alla oleva taulukko havainnollistaa tätä:
luku 30 31 32 33 34 35 36 viimeinen numero 1 3 9 7 1 3 9 Pätee 2019 = 4 ⋅ 504 + 3. Siksi luvun 32019 viimeinen numero on sama kuin luvun 33 viimeinen numero.
On tärkeää ottaa huomioon, että jakso ei välttämättä ala heti, vaikka tällä kertaa se alkoikin heti. Esimerkiksi luvun 2 potenssien viimeiset numerot ovat 1, 2, 4, 8, 6, 2, 4, …, siis alussa on yksi ykkönen ennen toistuvaa jaksoa.
Aiheeseen liittyviä harjoituksia: linkki
(c) b1, …, bn ovat bittejä. Kuinka monta eri arvoyhdistelmää niillä on?
Tämän kaavan voi keksiä (tai muistaa) seuraavalla ajattelulla.
Jollei tehtävä vieläkään ratkea, kokeile tätä.
Niinpä, kun jokainen merkki täytyy käyttää täsmälleen yhden kerran, yhdellä merkillä saa yhden merkkijonon, kahdella erilaisella 1 ⋅ 2, kolmella erilaisella 1 ⋅ 2 ⋅ 3, neljällä erilaisella 1 ⋅ 2 ⋅ 3 ⋅ 4 ja niin edelleen. Lukua 1 ⋅ 2 ⋅ ... ⋅ n merkitään n! ja kutsutaan nimellä ns kertoma. Myös nollas kertoma on määritelty. Se on sellainen luku, että kun sen kertoo ykkösellä, saadaan 1!, siis 1 ⋅ 0! = 1!. Ilmoita seuraavat kertomat.
| 0! = | |
| 1! = | |
| 2! = | |
| 3! = | |
| 4! = | |
| 5! = | |
| 6! = |
(d) Täydennä seuraava ohjelma siten, että se testaa, onko taulukon T[1…n] sisältö palindromi eli sama etu- ja takaperin.
Vastauksen voi keksiä seuraavalla ajattelulla.
Ohjelma testaa taulukon alkioita pareittain. Jos yksikin testattu pari koostuu erisuuruisista alkioista, niin ohjelma lopettaa vastauksella false. Jos näin ei koskaan käy, niin ohjelma lopettaa vastauksella true kun kaikki parit on testattu. Tehtävänä on selvittää sen alkion indeksi, joka testataan alkion i parina.
Taulukon ensimmäinen alkio pitää testata taulukon viimeistä alkiota vastaan, toinen alkio pitää testata toiseksi viimeistä alkiota vastaan ja niin edelleen. Missä kohdassa sijaitsevaa alkiota vastaan kohdan i alkio pitää testata?
| tässä sijaitseva testataan | tässä sijaitsevaa vastaan |
| 1 | |
| 2 | |
| 3 | |
| i |
Yhdellä pielessä olevaa vastausta n − i tuli paljon. Sen ykkösen saa tämäntapaisissa tehtävissä kohdalleen valitsemalla jonkin i:n arvon jolla luvut ovat helppoja ja huolehtimalla, että vastaus antaa sille oikean luvun. Tässä esimerkissä taulukon ensimmäinen indeksi on 1 ja viimeinen on n, joten kun i = 1 pitää vastauksen tuottaa n.
Tämäkin kikka kannattaa osata ja pitää työkalupakissa käyttövalmiina. Sille on valtavasti sovelluskohteita esimerkiksi ohjelmoitaessa. Vaikka yksittäistapauksen saaminen kohdalleen ei takaa että vastaus on oikein, se usein parantaa olennaisesti mahdollisuutta että vastaus on oikein. Siksi yksittäistapauksilla testaaminen kannattaa.
Aiheeseen liittyviä harjoituksia: linkki
(e) Ohjelman ylimmän rivin n voidaan korvata pienemmällä arvolla niin että ohjelma toimii silti oikein. Mikä on pienin tällainen arvo?
VihjeJos vastaus on true, niin ohjelma vertaa ensimmäisenä onko T[1] ≠ T[n] ja viimeisenä onko T[n] ≠ T[1]. Viimeinen vertailu on eripäin kuin ensimmäinen, mutta tuottaa silti saman tuloksen. Siksi viimeinen vertailu on hyödytön. Toisena ohjelma vertaa onko T[2] ≠ T[n − 1] ja toiseksi viimeisenä onko T[n − 1] ≠ T[2], ja niin edelleen. Jokaisen tällaisen parin jälkimmäinen vertailu on hyödytön. Ne voi jättää pois pienentämällä sitä arvoa, jonka kohdalla for-silmukka lopettaa.
Mitä tapahtuu keskellä taulukkoa, jos n on pariton?Jos n on pariton, niin ohjelma vertaa keskimmäistä alkiota itseensä ja vain yhden kerran. Esimerkiksi jos n = 5, niin ohjelma tekee vertailun T[3] ≠ T[3] täsmälleen yhden kerran. Tarvitseeko keskimmäistä alkiota verrata itseensä?Ei tarvitse, koska jokainen sellainen vertailu tuottaa false riippumatta taulukon sisällöstä. Esimerkiksi T[3] ≠ T[3] tuottaa false.
Edellä päätellyn perusteella oikea vastaus on suunnilleen selvä, mutta ”yhdellä pielessä” -tyyppisten virheiden vaara vaanii nytkin. Sen välttämiseksi kokeilemme muutamalla pienellä n:n arvolla. Ilmoita suurin i:n arvo, jolla testi T[i] ≠ T[…] tarvitsee tehdä.
| n | for-silmukan lopetusarvo |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 1 | |
| 0 | |
| n |
(f) Mitä hyötyä korvaamisesta on?
MallivastausOhjelma nopeutuu melkein kaksinkertaiseksi silloin kun vastaus on true.
3. Mitkä seuraavista kokonaislukuja koskevista päättelyaskelista ovat päteviä? Anna epäpäteville vastaesimerkki ja päteville lyhyt perustelu.
(a) nm > 0 ⇒ n > 0
MallivastausEi, koska jos n = m = −1, niin nm = 1 > 0 mutta ei n > 0.
Päättelemisen peruskäsitteistä ei vielä ole kunnollista tehtäväsivua, joten käsittelemme tässä niitä hieman.
Päättelyissä käsitellään väitteitä. Väitteissä on usein (mutta ei aina) vapaita muuttujia. (Kerron myöhemmin muuttujista, jotka eivät ole vapaita. Siihen saakka kaikki esimerkeissä esiintyvät muuttujat ovat vapaita.)
| 1 |
| n |
| 1 |
| n |
| 1 |
| 0 |
| 1 |
| 0 |
Jos vapaita muuttujia sisältävää väitettä sanotaan todeksi ilman että samalla annetaan vapaille muuttujille arvot, niin tarkoitetaan, että väite on tosi kaikilla mahdollisilla vapaiden muuttujien arvoyhdistelmillä. Toisin sanoen, vapaita muuttujia sisältävä väite on tosi jos ja vain jos sille ei ole vastaesimerkkejä. Esimerkiksi |x| ≥ 0 on tosi mutta |y| ≥ 3 ei ole, koska y = 1 on sille vastaesimerkki.
Jos väitteessä ei ole vapaita muuttujia, niin tulkitsemme, että silloin vapailla muuttujilla on täsmälleen yksi arvoyhdistelmä. Tämä arvoyhdistelmä on vastaesimerkki jos ja vain jos väite ei ole tosi. Tämän tulkinnan ansiosta äskeinen huomio yksinkertaistuu seuraavaan muotoon: väite on tosi jos ja vain jos sille ei ole vastaesimerkkejä.
| 1 |
| 2 |
Väitteiden totuusarvoihin liittyviä harjoituksia: linkki
Olkoot V1 ja V2 väitteitä. Päättelyaskel V1 ⇒ V2 tarkoittaa, että kaikilla niillä vapaiden muuttujien arvoyhdistelmillä, jotka ovat mahdollisia puheena olevassa asiayhteydessä ja joilla V1 on tosi, myös V2 on tosi.
Päättelyaskel ei ole tosi, epätosi eikä määrittelemätön. Päättelyaskel on joko pätevä tai epäpätevä (eli virheellinen).
Ainoa tapa, jolla V1 ⇒ V2 voi olla virheellinen, on että on olemassa muuttujien arvoyhdistelmä, jonka asiayhteys sallii ja jolla V1 on tosi mutta V2 ei ole tosi. Sellaista arvoyhdistelmää sanotaan ⇒-muotoisen päättelyaskeleen vastaesimerkiksi. Siis V1 ⇒ V2 on pätevä jos ja vain jos sille ei ole vastaesimerkkejä.
Merkitse ruutuihin TT, FF tai UU sen mukaan ovatko väitteet tosi, epätosi vai määrittelemätön. Valitse ne rivit, jotka sisältävät vastaesimerkin päättelyaskeleelle nm > 0 ⇒ n > 0.
| n | m | nm > 0 | n > 0 |
| 2 | 3 |
| 2 | 0 |
| 2 | −3 |
| 0 | 3 |
| 0 | 0 |
| 0 | −3 |
| −2 | 3 |
| −2 | 0 |
| −2 | −3 |
Päättelyaskel voi olla myös muotoa V1 ⇔ V2. Se tarkoittaa, että kun valitaan mikä tahansa asiayhteyden sallima vapaiden muuttujien arvoyhdistelmä, niin joko molemmat tai ei kumpikaan väitteistä V1 ja V2 ovat tosia. Toisin sanoen, se tarkoittaa samaa kuin V1 ⇒ V2 ja V2 ⇒ V1 yhdessä. Myös tämänmuotoinen päättelyaskel on pätevä jos ja vain jos sille ei ole vastaesimerkkejä. Tässä tapauksessa vastaesimerkki on muuttujien arvoyhdistelmä, jolla toinen puoli on mutta toinen puoli ei ole tosi.
Kannattaa siis takoa päähän:
Päättelyaskel on pätevä jos ja vain jos sille ei ole vastaesimerkkejä.
Jotta tätä voisi tarpeen tullen hyödyntää, kannattaa takoa päähän myös, mitä väitteen vastaesimerkki, ⇒-askeleen vastaesimerkki ja ⇔-askeleen vastaesimerkki tarkoittavat.
(b) n < m ≤ n + 1 ⇒ m = n + 1
MallivastausOn, koska kokonaislukua n suuremmat kokonaisluvut ovat n + 1, n + 2, …, ja niistä vain n + 1 toteuttaa ehdon m ≤ n + 1.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
Perustelemiseksi täytyy osoittaa, että jos n < m ≤ n + 1 on tosi, niin myös m = n + 1 on tosi. Jos n < m ≤ n + 1 on tosi, niin n < m, joten m = n + 1 tai m = n + 2 tai … koska kyse on kokonaisluvuista. Toisaalta n < m ≤ n + 1 lupaa myös, että m ≤ n + 1. Nämä kaksi yhdessä varmistavat, että m = n + 1 on tosi.
Sen lisäksi että päättelyaskel voi olla pätevä tai epäpätevä, se voi olla myös hyvin tai huonosti perusteltu. Päättelyaskel on hyvin perusteltu, jos ja vain jos se on niin yksinkertainen että lukija näkee miksi se on pätevä, tai hänelle annetaan niin paljon lisätietoa että hän ymmärtää miksi se on pätevä. Lukija voi olla varma, että päättelyaskel on pätevä vain jos se on perusteltu hyvin.
Siksi ihanne on, että päättelyaskeleet pitää perustella hyvin. Valitettavasti asia ei ole yksinkertainen. Koska toinen lukija ymmärtää vähemmällä kuin toinen, perustelun hyvyys ei ole matemaattisen tarkka käsite vaan sumea.
Matemaattisissa päättelyissä ei yleensä esitetä niitä yksityiskohtia, jotka kokenut lukija pystyy helposti itse keksimään. Muuten tekstistä tulisi pitkä, ja sen suuret linjat hukkuisivat lukuisien pikkuasioiden alle. Lukijan, joka on sillä matematiikan alueella aloittelija, voi olla työlästä tai jopa mahdotonta lukea tällaista päättelyä, vaikka hän olisi vahva jollain toisella matematiikan alueella.
Jos tenttikysymyksessä pyydetään lyhyttä perustelua, niin vastauksessa kannattaa keskittyä olennaisimpiin syihin miksi väite on tosi tai päättelyaskel on pätevä. Se on varmin keino saada pisteitä.
Tämän kohdan tapauksessa päättelyaskel ei ole pätevä reaaliluvuille mutta on pätevä kokonaisluvuille. Siksi perustelussa on tärkeää vedota siihen, että kyse on kokonaisluvuista. Tenttilomakkeessa annettu vastaustila riittää sen sanomiseen, että välillä n < x ≤ n + 1 ei ole muita kokonaislukuja kuin n + 1. Edellä ruskean sanan ”Selitys” alla on pitempi perustelu, joka yrittää olla riittävä silloin kun lukijana on tämän kurssin opiskelija.
(c) n2 < 0 ⇒ 0n = 3
MallivastausOn, koska vasen puoli on aina epätosi.
Edellä todettiin, että päättelyaskel on pätevä jos ja vain jos sille ei ole vastaesimerkkejä. Siitä seuraa, että jokainen sellainen ⇒-askel on pätevä, jonka vasen puoli ei ole koskaan tosi.
Tämä voi olla yllättävää. Niksi on siinä, että se voi johtaa omituisiin lopputuloksiin, mutta vain sellaisten asioiden tapauksessa, joita ei ole olemassa. Voidaan todistaa, että jokainen pyöreä neliö on kolmikulmainen, mutta tästä ei ole haittaa, koska pyöreitä neliöitä ei ole olemassa. Olemassa oleville asioille saadaan vain oikeita johtopäätöksiä.
On ollut tarpeellista rakentaa logiikka tällaiseksi. Usein on vaikeaa selvittää, onko jokin väite totta missään tilanteessa. Jos ⇒-askeleen pätevyyden määritelmä sisältäisi vaatimuksen, että vasemman puolen täytyy voida olla totta, niin pätevyyden perusteleminen vaikeutuisi huomattavasti aivan turhaan. Myöskään niin sanottuja ristiriitatodistuksia ei voitaisi käyttää. Ristiriitatodistus on tyyppiä ”jos V1 ei olisi tosi, niin siitä seuraisi V2, mutta V2 on mahdoton, joten V1 on tosi”.
Sievennä seuraavat väittämät mahdollisimman lyhyeen muotoon.
(d) ¬P ∧ ¬Q ⇔
Logiikassa on pieni määrä kaavoja, jotka kannattaa osata ulkoa. De Morganin kaavat kuuluvat niihin. Tehtävän vastaus saadaan tällä De Morganin kaavalla¬(P ∨ Q) ⇔ ¬P ∧ ¬Q.
Jos herää epäilys, muistinko kaavan oikein, kannattaa soveltaa sitä johonkin tuttuun tilanteeseen. Voidaan valita vaikka, että P tarkoittaa ”otan kahvia” ja Q tarkoittaa ”otan pullaa”. Silloin ¬P ∧ ¬Q tarkoittaa, että en ota kahvia ja en ota pullaa. Siis en ota kumpaakaan, en kahvia enkä pullaa. Vastaavasti ¬(P ∨ Q) tarkoittaa, että ei ole niin että otan kahvia tai otan pullaa. Sekin tarkoittaa että en ota kumpaakaan, en kahvia enkä pullaa. Siksi ¬(P ∨ Q) tarkoittaa samaa kuin ¬P ∧ ¬Q ja on oikea vastaus.
Toisaalta ¬(P ∧ Q) tarkoittaa, että ei ole niin että otan kahvia ja otan pullaa. Se kieltää sen että otan molempia ja sallii kolme vaihtoehtoa: otan pelkästään kahvia, otan pelkästään pullaa tai en ota kumpaakaan. Koska se sallii että otan pelkästään kahvia, se on eri asia kuin ¬P ∧ ¬Q joka tarkoittaa että en ota kumpaakaan. Siksi ¬(P ∧ Q) olisi väärä vastaus.
Aiheeseen liittyviä harjoituksia: linkki
Perustelen nyt, että lyhyempää oikeaa vastausta ei ole olemassa kuin ¬(P ∨ Q). Jos sekä P että Q ovat epätosi, niin ¬P ∧ ¬Q on tosi. Jos P vaihdetaan todeksi, niin ¬P ∧ ¬Q muuttuu epätodeksi. Samoin käy jos P pidetään epätotena mutta Q vaihdetaan todeksi. Näin ollen kaavan ¬P ∧ ¬Q totuusarvo riippuu sekä P:stä että Q:sta. Siksi jokaisessa kaavassa, joka sanoo saman asian kuin ¬P ∧ ¬Q, esiintyy sekä P että Q. Lyhyempiä sellaisia kaavoja on vain kahdeksan: P ∧ Q, P ∨ Q, P → Q, P ↔ Q ja samat toisinpäin. Jokaisesta voi nopeasti todeta, että se ei sano samaa kuin ¬P ∧ ¬Q.
Tentissä vastaajan ei kuitenkaan tarvitse perustella, että lyhyempää oikeaa vastausta ei ole olemassa, koska sitä ei kysytty. Opiskelija voi kirjoittaa lyhimmän keksimänsä kaavan joka sanoo oikean asian, ja toivoa että se olisi lyhin mahdollinen tai että se tuottaisi edes osan pisteistä, jos vielä lyhyempi kaava on olemassa.
(e) ¬P ∨ (Q ∨ P) ∧ R ⇔
Tentin vuonna kurssilla ei käsitelty määrittelemätöntä totuusarvoa U. Siksi tentissä oletettiin, että se ei ole käytössä.
Tämän ratkaiseminen kannattaa aloittaa havainnosta, että se on muotoa ¬P ∨ (…). Jos P on epätosi, koko kaava on tosi riippumatta siitä, mitä (…) on. Jos P on tosi, koko kaava tuottaa sen mitä (…) tuottaa. Koska (…) on (Q ∨ P) ∧ R, niin kun P on tosi se tuottaa (Q ∨ T) ∧ R eli T ∧ R eli R. Ei tarvitse käsitellä tapausta jossa P on määrittelemätön, koska tentissä oletettiin, että U ei ole käytössä. Tehtävän kaava tarkoittaa siis samaa kuin …¬P ∨ R.
Voiko sen saada vielä lyhyemmäksi?Kyllä voi: P → R. Kukaan tenttiin vastanneista ei ollut huomannut tätä. Onneksi täyden pisteen sai myös vastauksella ¬P ∨ R.
Aiheeseen liittyviä harjoituksia: linkki (linkki)
(f) n < 2 ∧ m > 5 ∨ ¬(m < n ∨ n = m) ⇔
 Nyt kaava on muotoa (n < 2 ∧ m > 5) ∨ (…)m > n.
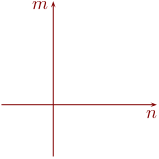
Sen kummastakin puolesta kannattaa piirtää kuva.
Piirrämme ensin n < 2 ∧ m > 5.
Sitä varten kopioi oheinen koordinaatisto kynällä paperille.
Sitten lisää siihen katkoviivalla suora n = 2.
Tuloksen pitäisi näyttää tältä
Nyt kaava on muotoa (n < 2 ∧ m > 5) ∨ (…)m > n.
Sen kummastakin puolesta kannattaa piirtää kuva.
Piirrämme ensin n < 2 ∧ m > 5.
Sitä varten kopioi oheinen koordinaatisto kynällä paperille.
Sitten lisää siihen katkoviivalla suora n = 2.
Tuloksen pitäisi näyttää tältä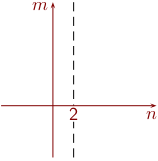 .
Lisää kuvaan m = 5
.
Lisää kuvaan m = 5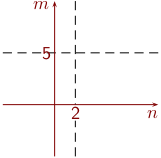 .
Tummenna alue n < 2 ∧ m > 5
.
Tummenna alue n < 2 ∧ m > 5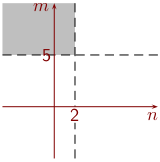 .
.
Nyt piirrämme kuvan osuudesta (…)m > n.
Vihje 1Kopioi oheinen koordinaatisto uudelleen.
Piirrä kopioon katkoviivalla suora n = m.
Vihje 2Tummenna se puoli, jolla n < m eli m
> n.
Tummennettavan puolen tunnistamiseksi etsi jokin piste, jossa m >
n.
Piste m = 1 ja n = 0 kelpaa.
Tuloksen pitäisi näyttää tältä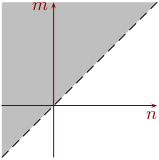 .
.
Kun molemmat kuvat laitetaan päällekkäin, niin saadaan
tällainen kuva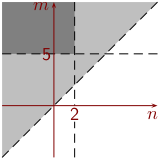 .
Tehtävän vastaus on siitä poimittavissa.
.
Tehtävän vastaus on siitä poimittavissa.
Nyt kun vastaus tiedetään, on helppo jälkiviisaana nähdä, että se olisi ollut pääteltävissä ilman kuvien piirtämisen vaivaa: jos n < 2 ∧ m > 5, niin …n < 2 < 5 < m, joten n < m. Niinpä aina kun n < 2 ∧ m > 5 on tosi, myös n < m on tosi, joten n < 2 ∧ m > 5 ∨ n < m ⇔ n < m.
n > 0 ∧ ∀ i; 2 ≤ i ≤ n: T[i] < 0
MallivastausMuut kuin ensimmäinen alkio ovat negatiivisia. (Tätä voi täydentää toteamuksella, että ensimmäinen alkio on olemassa. Myös voi olla hyvä mainita, että ei oteta kantaa siihen, onko ensimmäinen alkio negatiivinen.)
Suomennoksessa tavoitellaan ilmausta, joka on ihmisille mahdollisimman selkeä ja luonteva mutta samalla asiasisällön osalta mahdollisimman tarkka. Ilmaus ”n on suurempi kuin nolla ja jokaisella i joka on vähintään kaksi ja enintään n pätee että T[i] on pienempi kuin nolla” ei ole suomennos vaan kaavan lukeminen sanoilla sellaisenaan.
Osuus n > 0 tarkoittaa, että taulukko T ei ole tyhjä. Mallivastauksessa tätä ei sanota erikseen, koska osuus ”Muut kuin ensimmäinen” vihjaa melko selvästi, että ensimmäinen alkio on olemassa eli että T ei ole tyhjä. Sen saa kuitenkin sanoa erikseen varmuuden vuoksi, koska eri ihmiset tulkitsevat luonnollisen kielen ilmauksia eri tavoilla.
Ei ole olemassa selvää rajaa sille, milloin luonnollisen kielen ilmaus sanoo asiasisällön tarkasti oikein. Matemaattisia merkintöjä on kehitetty juuri siksi, että asioita voitaisiin ilmaista yksikäsitteisen tarkasti ja samalla tiiviisti. Niitä harjoitellaan tällä kurssilla siksi, että tarkkuus ja yksikäsitteisyys ovat olennaisia ohjelmien vaatimusmäärittelyssä.
Osuus ∀ i; 2 ≤ i ≤ n: tarkoittaa, että i käy läpi arvot 2, 3, …, n ja kaksoispisteen jälkeen väitetty asia pätee niistä jokaiselle. Tässä i on sidottu eikä vapaa muuttuja. Muuttujat n ja T ovat vapaita. Niiden arvot tulevat väittämän ulkopuolelta. Tehtävän predikaatti on tosi esimerkiksi silloin kun n = 3 ja T = [1, −2, −3] ja epätosi esimerkiksi silloin kun n = 4 ja T = [1, −2, 3, −1]. Siis n ja T saavat arvonsa siitä taulukosta, josta kulloinkin puhutaan. Sama ei päde i:hin, vaan se saa arvonsa osuudesta ∀ i; 2 ≤ i ≤ n:. Siis i on väittämän sisäinen apumuuttuja.
Kaksoispisteen jälkeen lukee T[i] < 0, mikä tarkoittaa, että kohdassa i sijaitseva alkio on negatiivinen. Siis ∀ i; 2 ≤ i ≤ n: T[i] < 0 tarkoittaa, että kohdissa 2, 3, …, n sijaitsevat alkiot ovat kaikki negatiivisia. Koska taulukon indeksointialueeksi on ilmoitettu 1…n, edellä mainitut kohdat kattavat taulukon kaikki muut alkiot paitsi ensimmäisen. Siis muut kuin ensimmäinen alkio ovat negatiivisia.
Alkion T[1] arvosta ei sanota mitään. Siksi se voi olla negatiivinen, mutta se voi olla myös ei-negatiivinen.
Aiheeseen liittyviä harjoituksia: linkki
Esitä seuraavat taulukosta T[1…n] puhuvat väittämät predikaatteina.
(b) Luku 5 esiintyy siinä ainakin kahdesti.
Sitten lisätään ilmaus, joka sanoo, että 5 esiintyy toisenkin kerran. Samanlainen ilmaus kuin äsken kelpaa, mutta joudutaan käyttämään eri muuttujaa. Saadaan …∃ j; 1 ≤ j ≤ n: T[j] = 5 Täytyy myös sanoa, että edellä mainittu ja tämä paikka ovat eri paikat, eli …i ≠ j Koska siinä käytetään molempia muuttujia, se täytyy sijoittaa siten, että se on molempien kvanttorien vaikutuspiirissä. Koska eri osien täytyy olla yhtäaikaa voimassa, ne yhdistetään operaattorilla …∧
Vastausta saa lyhennettyä näinRajaa molemmat muuttujat samalla rajaajalla siten, että toinen muuttuja ilmaisee ensimmäisen ja toinen jälkimmäisen paikan..
Aiheeseen liittyviä harjoituksia: linkki linkki
(c) Luku 5 esiintyy siinä täsmälleen kahdesti.
VihjeEdellisen kohdan vastaukseen lisätään osuus, joka sanoo, että kolmatta kohtaa ei ole, jossa alkio on 5. Se voidaan sanoa esimerkiksi sanomalla, että jokaisella k, joka on laillisella alueella eikä ole i eikä j, kohdassa k oleva alkio ei ole 5.
5. (a) (2 pistettä) Kirjoita jakoyhtälö käyttäen sanoja ”div” ja ”mod”. Kerro millä välillä jakojäännös on.
Mallivastaus
n = m(n div m) + n mod m
0 ≤ n mod m < |m|
Lasten yhteensä saamien karkkien määrä voidaan ilmaista kahdella lyhyellä tavalla.
| ilman sanaa div | |
| ilman sanaa mod |
Sanoilla ilmaistuna: jaettava on yhtäsuuri kuin …jakaja kertaa osamäärä plus jakojäännös.
Kun jakaja on negatiivinen, niin jakojäännös ei voi olla äsken ilmoitetulla välillä, koska …ehdosta 0 ≤ n mod m < m seuraa 0 < m, mikä m:n ollessa negatiivinen on mahdotonta. Kun jakaja, jaettava tai molemmat saavat olla negatiivisia, niin asia on monimutkainen. Wikipediassa on hyviä kuvia ja paljon muuta tietoa. On olemassa ainakin kolme vakiintunutta käytäntöä:
- Jakojäännöksellä on sama etumerkki kuin jaettavalla. Osamäärä pyöristetään nollaa kohti, joten nollan ympärillä on alue, jossa osamäärä käyttäytyy epäsäännöllisesti. Siksi matematiikassa ei suosita tätä tapaa. Ohjelmointikielissä se on yleinen. Jakojäännös on merkistään riippuen välillä …0 ≤ n mod m < |m| tai välillä …−|m| < n mod m ≤ 0.
- Jakojäännöksellä on sama etumerkki kuin jakajalla. Osamäärä pyöristetään aina alaspäin. Monissa ohjelmointikielissä tämä on tarjolla eri nimellä kuin edellinen tapa ja joissakin ainoana vaihtoehtona. MathCheck noudattaa tätä tapaa — tai ainakin noudatti silloin, kun tämä teksti kirjoitettiin ☺ (kolmas tapa olisi ehkä matemaattisesti parempi — tai sitten ei, vaikea tietää). Jakojäännös on samalla välillä kuin edellisessä kohdassa.
- Jakojäännös on ei-negatiivinen. Tämä on matematiikassa suosittu tapa. Se on ohjelmointikielissä harvinainen, mutta esimerkiksi Dart % ja Maple mod toimivat niin. Jakojäännös on välillä …0 ≤ n mod m < |m|.
Oheinen taulukko havainnollistaa, miten sekava asia on ohjelmointikielissä. Se kertoo, minkä mukaan jakojäännöksen etumerkki valitaan. Sen tiedot on poimittu Wikipedian paljon isommasta taulukosta.
kieli jaettavan jakajan AppleScript mod C++ 2011 % C# % Haskell rem mod Java % Math.floorMod Perl % Python math.fmod % Ruby remainder() %, modulo()
Tärkeää on osata
- jakoyhtälön kaava ja
- jakojäännöksen väli silloin kun jakaja ja jaettava ovat ei-negatiivisia, sekä
- muistaa että negatiivisilla arvoilla tulos riippuu ohjelmointikielestä.
(b) (4 pistettä) Kirjoita ennalta miettimäsi essee alle tai eri paperille (saat sen pyytämällä, muista kirjoittaa sinne nimesi ja syntymäaikasi).
Kurssilla ei enää ole esseetä.