Tehtävä:
Viimeinen numero
Lyhyt MathCheck-ohje (uuteen välilehteen)
Tässä tehtävässä valmistaudutaan modulaarisen aritmetiikan opiskeluun tutkimalla, miten luvun viimeinen numero käyttäytyy laskutoimituksissa. Samalla aloitetaan tutustuminen ilmiöihin, joissa on alkuosa ja toistuva jakso.
Riippuu vain viimeisistä numeroista
Laske seuraavat yhteenlaskut vaikka laskimella.
Huomaathan, että jokaisen tuloksen viimeinen numero on 3?
Laske seuraavat kertolaskut vaikka laskimella.
Huomaathan, että jokaisen tuloksen viimeinen numero on 8?
Kahden kokonaisluvun yhteen-, vähennys ja kertolaskun tuloksen viimeinen numero riippuu vain kummankin luvun viimeisestä numerosta. Yhteen-, vähennys- ja kertolaskun tuloksen kaksi viimeistä numeroa riippuvat vain laskettavien kahdesta viimeisestä numerosta, kolme vain kolmesta ja niin edelleen. Mikä tahansa määrä yhteen-, vähennys ja kertolaskun tuloksen viimeisiä numeroita riippuu vain samasta määrästä alkuperäisten lukujen viimeisiä numeroita.
Kummassakin edellisistä lausekkeista on vain ne muuttujat, jotka sisältävät lukujen n ja N kaksi viimeistä numeroa. Olemme osoittaneet, että luvun n + N kaksi viimeistä numeroa riippuvat vain lukujen n ja N kahdesta viimeisestä numerosta.
Viimeinen numero voi saada vain 10 erilaista arvoa 0, 1, …, 9. Kaksi viimeistä numeroa voivat yhteensä saada vain 100 erilaista arvoa 00, 01, …, 09, 10, 11, …, 99. (Jos luvussa on vain yksi numero, siihen ajatellaan lisättäväksi etunolla. Esimerkiksi luvun 7 kaksi viimeistä numeroa ovat 07.) Kolme viimeistä numeroa voivat yhteensä saada vain 1000 erilaista arvoa, ja niin edelleen.
Alkuosa ja jakso
Jos otetaan mikä tahansa kokonaisluku lähtökohdaksi ja aletaan toistaa mitä tahansa laskutoimitusta, joka on muodostettu vain yhteen-, vähennys- ja kertolaskuista, niin viimeistään 100 toiston jälkeen kaksi viimeistä numeroa ovat samat kuin joskus aikaisemmin. Tämä johtuu siitä, että muutoin arvot loppuvat kesken. Sen jälkeen kaksi viimeistä numeroa alkaa toistaa samaa jaksoa. Siis ensin on alkuosa, jonka pituus on vähintään 0, ja sitten on jakso, jonka pituus on vähintään 1. Jos valitaan mahdollisimman lyhyet alkuosa ja jakso, niin niiden yhteispituus on enintään 100.
Varmistetaanpa, että ymmärsit, miten lukujono 0, 82, 492, 2542, 12792, 64042, … saatiin. Jos ymmärsit, niin seuraavista kohdista selviät kopioimalla yltä ja pudottamalla vastauslaatikkoon.
Edellä puhuttiin mahdollisimman lyhyistä alkuosasta ja jaksosta. Myös 00, 82, 92, 42, 92 on esimerkin alkuosa ja 42, 92, 42, 92 on jakso. Usein on yhdentekevää mitä alkuosaa ja jaksoa käytetään, kunhan ne on valittu siten, että jakso alkaa oikeasta kohdasta suhteessa alkuosaan. Jos esimerkiksi alkuosa on 00, 82, 92, niin jakso 42, 92, 42, 92 alkaa oikeasta kohdasta, mutta 92, 42, 92, 42 ei ala. Jakson valinnalla on merkitystä esimerkiksi silloin kun luvataan, että lyhyin jakso on korkeintaan jonkin pituinen.
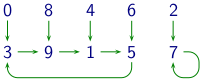 Tämä kuva näyttää jokaiselle numerolle, mihin numeroon siitä päädytään
laskemalla 2n + 3 ja ottamalla tuloksen viimeinen numero.
Huomaamme, että jos aloitetaan numerosta 2 tai 7, niin lopulta päädytään
toistamaan jaksoa 7, ja jos aloitetaan mistä tahansa muusta numerosta, niin
lopulta päädytään toistamaan jaksoa 3, 9, 1, 5.
Tässä kuvassa lyhyimpien alkuosan ja jakson yhteispituus on enintään 5.
Lyhyimpien jaksojen pituudet ovat 1 ja 4, ja lyhyimpien alkuosien pituudet
ovat 0 ja 1.
Tämä kuva näyttää jokaiselle numerolle, mihin numeroon siitä päädytään
laskemalla 2n + 3 ja ottamalla tuloksen viimeinen numero.
Huomaamme, että jos aloitetaan numerosta 2 tai 7, niin lopulta päädytään
toistamaan jaksoa 7, ja jos aloitetaan mistä tahansa muusta numerosta, niin
lopulta päädytään toistamaan jaksoa 3, 9, 1, 5.
Tässä kuvassa lyhyimpien alkuosan ja jakson yhteispituus on enintään 5.
Lyhyimpien jaksojen pituudet ovat 1 ja 4, ja lyhyimpien alkuosien pituudet
ovat 0 ja 1.
| 3 |
| 28 |
| 7 |
| 10 |
Viimeisen numeron laskemisesta
Jaksoja hyödyntämällä voi vähällä vaivalla laskea monen sellaisenkin laskun lopputuloksen viimeisen numeron, jotka tavalliseen tapaan laskettuina olisivat kovin työläitä. Tässäkään tärkeää ei ole oppia juuri tämä laskutoimitus, vaan oppia alkuosan ja jakson käyttöä yleisesti.
Ideaan kiinni pääsemiseksi laskemme ensin seuraavan: jos nyt kello on tasan 15, niin paljonko kello on miljoonan eli 1000000 tunnin kuluttua? Täysi vuorokausi on 24 tuntia. Miljoonaan menee jokin määrä q täysiä vuorokausia ja lisäksi jokin määrä r tunteja, missä r tekee vähemmän kuin vuorokauden:
1000000 = 24q + r, missä 0 ≤ r < 24
Jos laskimessasi on modulo-operaatio, luvun r saa sillä laskemalla r = 1000000 mod 24. Muussa tapauksessa sen saa seuraavasti:
- Laske jakolasku 1000000 / 24. Tulokseksi tulee 41666.666666667, missä desimaalien määrä ja viimeinen desimaali voivat riippua laskimesta.
- Hävitä jollain lailla luvun kokonaisosa. Laskimessa, jolla kokeilin, sen voi maalata ja pyyhkiä pois. Sen voi hävittää vähentämällä kokonaisosan, siis jatkamalla laskua −41666. Tai voi aloittaa kokonaan uuden laskun naputtelemalla desimaaliosan alkua tarpeeksi pitkälle. Riittää naputella yksi desimaali enemmän kuin jakajassa on. Nyt jakaja on 24. Siinä on kaksi desimaalia, joten riittää naputella 0.666.
- Kerro tulos jakajalla ja pyöristä lähimpään kokonaislukuun. Esimerkissämme 0.666 · 24 = 15.984, jota lähin kokonaisluku on 16.
- Voit harjoitella tätä muutamalla esimerkillä:
Miljoona tuntia eteenpäin on siis jokin määrä täysiä vuorokausia sekä 16 tuntia eteenpäin. Täysiä vuorokausia ei tarvitse ottaa huomioon, joten riittää lisätä tutkittavaan kellonaikaan 16, joten laskemme 15 + 16 = 31. Se ylittää 24 eli vie seuraavan vuorokauden puolelle, joten vähennämme 24 saaden 31 − 24 = 7. Kello 15:stä miljoonan tunnin päästä kello on siis tasan 7.
Tämän olisi voinut laskea näinkin: (15 + 1000000) mod 24 = 7. Laskimme hieman monimutkaisemmin siksi, että se tapa toimii silloinkin, kun yksinkertainen tapa johtaisi niin isoihin lukuihin, että laskin ei niistä selviä. Tästä esimerkiksi laskemme luvun 20272027 viimeisen numeron.
Edellä totesimme, että jos laskemme 20270, 20271, 20272, … niin viimeinen numero alkaa melko pian toistua. Teemme taulukkoa viimeisen numeron selvittämiseksi, kunnes viimeinen numero toistuu. Kunkin rivin oikeassa reunassa on vasemmassa reunassa mainitun luvun viimeinen numero. Se saadaan edellisen rivin viimeisestä numerosta kertomalla se kantaluvun eli 2027 viimeisellä numerolla eli 7, ja ottamalla tuloksesta viimeinen numero. Kertolaskun tulos näytetään rivin keskellä.
| luku | edellinen kertaa 7 | viimeinen numero |
|---|---|---|
| 20270 | 1 | |
| 20271 | 7 | 7 |
| 20272 | 49 | 9 |
| 20273 | 63 | 3 |
| 20274 | 21 | 1 |
Lyhyimmän jakson pituus on siis 4. Koska 20274 tuottaa saman viimeisen numeron kuin 20270, niin 20275 tuottaa saman viimeisen numeron kuin 20271, 20276 tuottaa saman viimeisen numeron kuin 20272 ja niin edelleen. Siksi 20278, 202712, ja niin edelleen tuottavat saman viimeisen numeron kuin 20274. Eksponentista 2027 tulee jokin määrä jaksoja ja niiden lisäksi 2027 mod 4 = 3 kertolaskua. Luvun 20272027 viimeinen numero on siis sama kuin luvun 20273 viimeinen numero.
Viedään tämä lasku loppuun ja harjoitellaan viisi muuta esimerkkiä, joista osa kantaa pitkälle tulevaisuuteen! Anna seuraavien lukujen viimeinen numero.
Näissä tapauksissa ensimmäisen rivin viimeinen numero alkoi toistua. Näin ei käy aina. Jos näin ei käy, niin täytyy huolehtia, että lopputuloksen viimeinen numero katsotaan sellaisella eksponentilla, jossa toisto on varmasti alkanut. Esimerkiksi lukujen 20280, 20281, … viimeinen numero on 1, 8, 4, 2, 6, 8, …. Lyhyimmän jakson pituus on siis 4. Huomaamme, että 2028 mod 4 = 0. Kuitenkaan luvun 20282028 viimeinen numero ei ole luvun 20280 viimeinen numero eli 1, koska toisto ei ole vielä alkanut eksponentin 0 kohdalla. Eksponenttia pitää kasvattaa nelosella niin monta kertaa, että toisto alkaa. Yksi kerta riittää, joten luvun 20282028 viimeinen numero on sama kuin luvun 20284 viimeinen numero eli 6.
Anna seuraavien lukujen viimeinen numero.
Olemme laskeneet jo yli puolet 2020-luvun tehtävistä. Ei kai me jätetä hommaa kesken, eiköhän lasketa loputkin? Nyt kerää energiaa yli-inhimilliseen ponnistukseen! Laske seuraavien lukujen viimeiset numerot:
Mikä riippuu muustakin?
Jakolaskun lopputuloksen viimeinen numero voi riippua muustakin kuin jakajan ja jaettavan viimeisestä numerosta. Aivan kohta tehtäväsi on antaa tästä kaksi esimerkkiä. Sitä ennen kuitenkin varmistamme, että tiedät, mitä tarkoittaa, että kokonaislukujen jakolasku menee tasan. Se tarkoittaa, että lopputuloskin on kokonaisluku.
Käytimme tässä tehtävässä viimeistä numeroa siksi, että se on havainnollinen. Saamamme taulukko pätee kuitenkin moduloaritmetiikassa yleisesti. Esimerkiksi luku (nm) mod M riippuu vain luvuista n mod M ja m mod M. Viimeisen numeron tapaus saadaan tästä valitsemalla M = 10.