Differential geometry 2023

I will teach an introduction to differential geometry that consits of two subsequent courses:

Current affairs 27.11.2023

A preliminary final version of the lecture notes (in Finnish) is now posted below.

Introduction to manifolds 2023

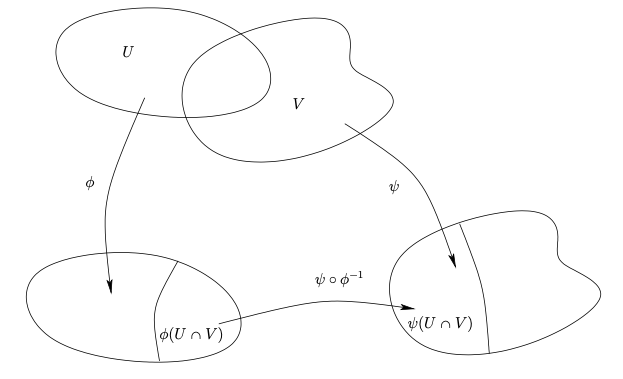
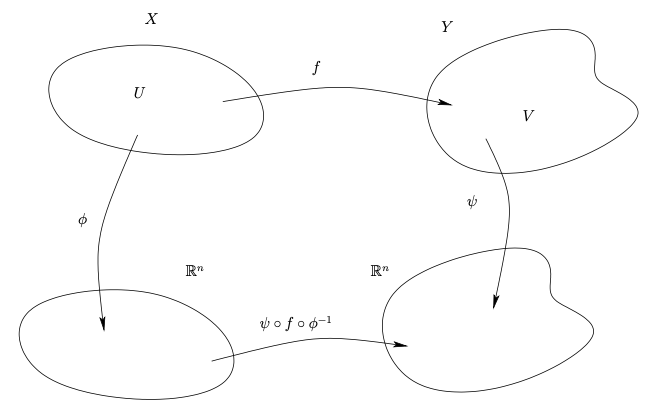
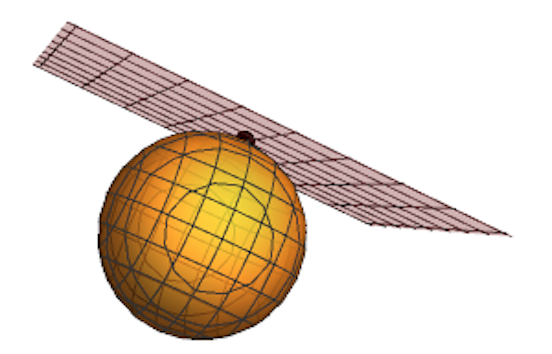
This course is an introduction to the basic objects of differential geometry. The material is presented in the context of abstract $\rm C^\infty$-smooth manifolds.

A Hausdorff $N_2$-space $M$ is a differentiable manifold of dimension $n$ if it has an atlas of local coordinate maps defined on open subsets of $M$ such that if $\phi\colon U\to\mathbb R^n$ and $\psi\colon V\to\mathbb R^n$ are local coordinate maps, the composition $\psi\circ \phi^{-1}$ is a smooth diffeomorphism onto its image. As examples, we discuss submanifolds of $\mathbb R^n$ such as the sphere $\mathbb S^{n-1}$, products of differentiable manifolds such as $\mathbb S^1\times\mathbb S^1$, and suitable quotient spaces of differentiable manifolds.

kuva kuva

If $M$ and $N$ are differentiable manifolds, we use the local coordinate mappings to define what it means for a mapping $f\colon M\to N$ to be smooth. We define tangent vectors and tangent spaces of a differentiable manifold, and the tangent mapping of a differential mapping between differentiable manifolds.

kuva

For example, a tangent vector of $\mathbb R^n$ at a point $x$ can be used to compute the directional derivative of any smooth function whose domain of definition contains $x$. We generalize this and define that a tangent vector of differentiable manifold $M$ at a point $p\in M$ is a derivation of smooth functions whose domain of definition contains $p$. The derivations at a point $p\in M$ form the tangent space $T_pM$, and the union of the tangent spaces forms the tangent bundle $TM$. Vector fields appear as global derivations of smooth functions or, equivalently as sections of $TM$.

Prerequisites

The prerequisite courses are Vektorianalyysi 1 and 2 or Käyrien ja pintojen differentiaaligeometria, and Topologia. This translates to differential calculus of several variables and topology.

It is possible to take these courses even if you have not taken a course on topology but it is strongly recommended that you should take topology this year. For self-study, I recommend my lectures (in Finnish) Metriset avaruudet ja topologia or, for example J. Munkres: Topology.

Reading material

Differential geometry on manifolds 2023

This course continues from where Introduction to manifolds stops. We introduce cotangent vectors that form the dual of the tangent space at a point of a differentiable manifold, and we construct the cotangent bundle. We discuss tensor fields and differential forms on differentiable manifolds and the required background material on multilinear algebra.

Prerequisites

Introduction to manifolds

Lectures

A preliminary version of the text of the course (in Finnish) is here: Differentiaaligeometria 2023 (30.11.2023).

Exercises

Suomenkielisten tehtävien numerointi on materiaalin uusimman version mukainen.

Introduction to manifolds
1 1.1, 1.2, 1.5-1.7 Problem sheet 1 with solutions
2 1.8, 1.11, 2.2, 2.3, 2.5, 2.7. Problem sheet 2 with solutions
3 2.6-2.10, 3.1. Problem sheet 3 with solutions
4 3.2, 3.3, 3.5, 3.6, 3.8 Problem sheet 4 with solutions
5 4.2-4.6 Problem sheet 5 with solutions
6 5.1, 5.2, 5.4, 5.9, 5.10 Problem sheet 6 with solutions
Differential geometry on manifolds
76.2, 6.3, 6.6, 6.8, 6.9 Problem sheet 7 with solutions
86.10-6.12, 7.1, 7.2, 7.5 Problem sheet 8 with solutions
97.6, 7.7, 7.9, 7.13, 8.1, 8.2 Problem sheet 9 with solutions
107.10-7.12, 8.3, 8.4, 8.6 Problem sheet 10 with solutions
119.2, 9.3, 9.5, 9.7, 9.8 Problem sheet 11 with solutions
1210.1, 10.4-10.6, 10.9 Problem sheet 12 with solutions

Contact information

Jouni Parkkonen
Matematiikan ja tilastotieteen laitos
PL 35
40014 Jyväskylän yliopisto