scode <- "
data {
int<lower=0> n; // havaintojen lukumäärä
int<lower=0> m; // sensuroimattomien havaintojen lukumäärä
real a; // sensuroinnin raja
real y[m]; // havainnot
}
parameters {
real<lower=0> theta;
}
model {
theta ~ gamma(1, 1);
y ~ exponential(theta);
target += (n-m) * exponential_lccdf(a | theta);
// eksponenttijakauman komplementaarisen kumulatiivisen jakaumafunktion
// eli eksponenttijakauman elossaolofunktion logaritmi
}
"
# Poimitaan sensuroimattomat havainnot erilleen
device_obs <- device[device$time < 8, ]
# Kaikkien ja sensuroimattomien havaintojen lukumäärät
n <- nrow(device)
m <- nrow(device_obs)
# Sensuroinnin raja datassa
a <- 8.0
fit <- stan(
model_code = scode,
data = list(n = n, m = m, a = a, y = device_obs$time),
iter = 2000,
verbose = FALSE
)5 Regressiomalleja
5.1 Sensuroidut havainnot
Sensurointi on mahdollista ottaa huomioon posteriorin määrittämisessä. Tarkastellaan sensuroinnin käsittelyä esimerkkien avulla:
Esimerkki 5.1 (Eksponenttijakautunut elinaika) Oletetaan, että havaintoihin \(y_1,\ldots,y_n\) liittyvät seuraavat oletukset.
Havainnot noudattavat jakaumaa \(\operatorname{Exp}(\theta)\) jollakin \(\theta > 0\).
Havainnot ovat ehdollisesti riippumattomia ehdolla \(\theta\), ts. ne ovat vaihdannaisia.
Havainnoinnissa on tehty sensurointi oikealta tunnettuun arvoon \(a > 0\): Jos \(y_i \leq a\), havainto tehdään ja jos \(y_i > a\), niin havainto on sensuroitu (niistä pidetään lukua).
Näistä oletuksista ensimmäinen koskee populaatiojakaumaa, kun taas oletukset 2–3 koskevat havainnointia. Tällöin saadaan \[ p(y | \theta) = \prod_{y_i \leq a} p(y_i | \theta) \times \prod_{y_i > a} S(a | \theta), \] missä \(S(a | \theta) = P(y_i > a | \theta)\) on elossaolofunktio. Siten \[ p(y_1,\ldots,y_n | \theta) = \prod_{i=1}^m \left[\theta e^{-\theta y_i} \right] \times \left[e^{-\theta a}\right]^{n-m} = \theta^m e^{-\theta\left[\sum_{i=1}^m y_i + (n - m)a\right]}, \] missä \(m\) on sensuroimattomien havaintojen lukumäärä (ja \(n-m\) on sensuroitujen havaintojen lukumäärä).
Oletetaan, että \(\theta\) noudattaa gammajakaumaa \(\textrm{Gamma}(\alpha,\beta)\). Silloin \[ \begin{aligned} p(\theta|\alpha,\beta) &= \frac{ \beta^\alpha }{ \Gamma(\alpha) } \theta^{\alpha-1} e^{-\beta \theta} \\ &\propto \theta^{\alpha-1} e^{-\beta \theta},\,\theta > 0. \end{aligned} \] Priorin myötä syntyy kaksi uutta parametria, gammajakauman muotoparametri \(\alpha\) ja käänteinen skaalaparametri \(\beta\). Näille tulee asettaa priori: jos \(\alpha\) ja \(\beta\) oletetaan a priori riippumattomiksi, niin silloin on määriteltävä \(p(\alpha)\) ja \(p(\beta)\), muulloin yhteisjakauma \(p(\alpha,\beta)\).
Oletetaan nyt, että \(\alpha\) ja \(\beta\) ovat a priori riippumattomia ja tunnettuja vakioita: \(\alpha = A\) ja \(\beta = B\). (Nämä ovat degeneroituneita jakaumia). Vaihdannaiset havainnot ovat \(y_1,\ldots,y_m\) ja \(n-m\) havaintoa on sensuroitu arvoon \(\alpha > 0\). Tällöin \[ \begin{aligned} p(\theta | y) &\propto \theta^m e^{-\theta\left[\sum_{i=1}^m y_i + (n - m)a \right]} \theta^{A-1} e^{-B \theta} \\ &= \theta^{A + m - 1}e^{-\theta\left[B + \sum_{i=1^m} y_i + (n-m)a \right]}, \end{aligned} \] kun \(\theta > 0\). Tämä jakauma on \[ \textrm{Gamma}(A + m, B + \sum_{i=1}^m y_i + (n-m)a). \]
Tarkastellaan seuraavaksi aineistoa device.dat, joka sisältää 50 eri laitteen käyttöajat vuosissa. Mikäli laite on ollut käytössä yli 8 vuotta, ei sen todellista käyttöaikaa ole havaittu. Käyttöaikojen oletetaan noudattavan jakaumaa \(\operatorname{Exp}(\theta)\). Sovitetaan nyt edellä kuvailtu malli Stanilla.
Parametrin \(\theta\) posteriorijakauman odotusarvo on 0.161 ja keskihajonta 0.027, ja 95 %:n posterioriväliksi saadaan (0.113, 0.217).
Posteriorijakaumaotoksen histogrammi ja teoreettisen Gamma-posteriorin kuvaaja (sinisellä):

Parametrin \(\theta\) otospolku lämmittelyjakson jälkeen yhdessä Stanin ketjuista on

Esimerkki 5.2 (Kemoterapia-aineisto) Tarkastellaan aineistoa, jossa kultakin potilaalta on mitattu elinaika hoidon aloittamisesta alkaen. Elinajat ovat osittain sensuroituja, ja koeasetelmassa on kaksi ryhmää, koeryhmä ja kontrolliryhmä. Kovariaattina on potilaan ikä. Kiinnostuksen kohteena on hoidon mahdollinen vaikutus elinaikaan. (chemo.dat)
On siis havaittu elinajat \(t_1, \ldots, t_n\), sensurointi \(\delta_1, \ldots, \delta_n\) sekä kovariaatit \(x_{ij}, \ldots, x_{nj}\), missä \(j = 1,\ldots,p\).
Sensurointimuuttuja \(\delta_i\) määritellään sellaiseksi, että \(\delta_i = 1\) jos havainto \(i\) on tehty sensuroimattomana, muuten \(\delta_i = 0\). Malli elinajoille on \[ \log t_i = \mu + \sum_{j = 1}^p \beta_j x_{ij} + \sigma \epsilon_i, \] Oletetaan, että virhetermit \(\epsilon_i\) ovat riippumattomia ja noudattavat tyypin 1 Gumbel-jakaumaa, jonka tiheysfunktio on \[ p(\epsilon) = \exp(\epsilon - \exp(\epsilon)). \] Gumbel-jakauman karakterisointeja:
log-Weibull -jakauma.
eräs GEV-perheen jakauma (generalized extreme value distribution).
kaksinkertainen eksponenttinen jakauma.
Mallissa on siis \(p + 2\) parametria: \(\mu,\sigma,\beta_1,\ldots,\beta_p\). Merkitään:
\(y_i = \log t_i\)
\(\beta = (\beta_1,\ldots,\beta_p)\)
\(z_i = (y_i - \mu - \sum_{j=1}^p \beta_j x_{ij})/\sigma\)
\(p_i(y_i|\beta,\mu,\sigma) = \frac{1}{\sigma}\exp(z_i - \exp(z_i))\)
\(S_i(y_i|\beta,\mu,\sigma) = \exp(-\exp(z_i))\) (elossaolofunktio)
Uskottavuudeksi saadaan \[ p(y|\beta,\mu,\sigma) = \prod_{i=1}^n \left[p_i(y_i|\beta,\mu,\sigma)^{\delta_i}\,S_i(y_i)^{1-\delta_i} \right]. \] Oletetaan, että parametrit ovat a priori riippumattomat. Valitaan
\(p(\beta_j) \propto 1,\, j = 1,\ldots,p\)
\(p(\mu) \propto 1\)
\(p(\sigma) \propto \frac{1}{\sigma}\)
Normeeraamaton posteriori on \[ p(\beta,\mu,\sigma|y) \propto \frac{1}{\sigma}p(y|\beta,\mu,\sigma). \] Posteriorijakauman avulla voidaan tutkia esimerkiksi käsittelyn vaikutusta, eri kovariaattien vaikutusta tai käsittelyryhmään kuuluvan henkilön selviytymistä. Mallin sovittaminen esimerkiksi JAGSissa vaatii erityistoimenpiteitä, sillä Gumbel-jakaumaa ei suoraan ole saatavilla. Tällöin voidaan nojata esimerkiksi ns. “nolla-yksi -temppuun”, joka esitellään luvussa @ref(sec:newdist). Stanissa Gumbel-jakauma on suoraan saatavilla, mutta sen parametrisointi poikkeaa edellä esitetystä. NIMBLEssä on mahdollista määritellä uusi jakauma.
5.2 Muutospisteongelma
Stokastisten prosessien ominaisuudet eivät välttämättä pysy vakioina ajan suhteen. Esimerkiksi prosessin odotusarvo, varianssi tai jonkin muu ominaisuus voi muuttua yllättäen. Muutospisteongelmalla tarkoitetaan yleisesti tilannetta, jossa jonkin prosessin parametrien osajoukon tiedetään muuttuvan vähintään kerran tietyn tarkastelujakson aikana. Tarkoituksena on tällöin selvittää ajanhetket, joissa muutokset tapahtuvat.
Esimerkki 5.3 (Hiilikaivosonnettomuudet) Seuraava aineisto kuvaa hiilikaivosonnettomuuksien määrää vuosina 1851–1962 (\(n = 112\), coal.dat).
| Vuosikymmen | Onnettomuuksien lukumäärä |
|---|---|
| 1851–1860 | 4, 5, 4, 1, 0, 4, 3, 4, 0, 6 |
| 1861–1870 | 3, 3, 4, 0, 2, 6, 3, 3, 5, 4 |
| 1871–1880 | 5, 3, 1, 4, 4, 1, 5, 5, 3, 4 |
| 1881–1890 | 2, 5, 2, 2, 3, 4, 2, 1, 3, 2 |
| 1890–1900 | 1, 1, 1, 1, 1, 3, 0, 0, 1, 0 |
| 1901–1910 | 1, 1, 0, 0, 3, 1, 0, 3, 2, 2 |
| 1911–1920 | 0, 1, 1, 1, 0, 1, 0, 1, 0, 0 |
| 1921–1930 | 0, 2, 1, 0, 0, 0, 1, 1, 0, 2 |
| 1931–1940 | 2, 3, 1, 1, 2, 1, 1, 1, 1, 2 |
| 1941–1950 | 4, 2, 0, 0, 0, 1, 4, 0, 0, 0 |
| 1951–1960 | 1, 0, 0, 0, 0, 0, 1, 0, 0, 1 |
| 1961–1962 | 0, 0 |
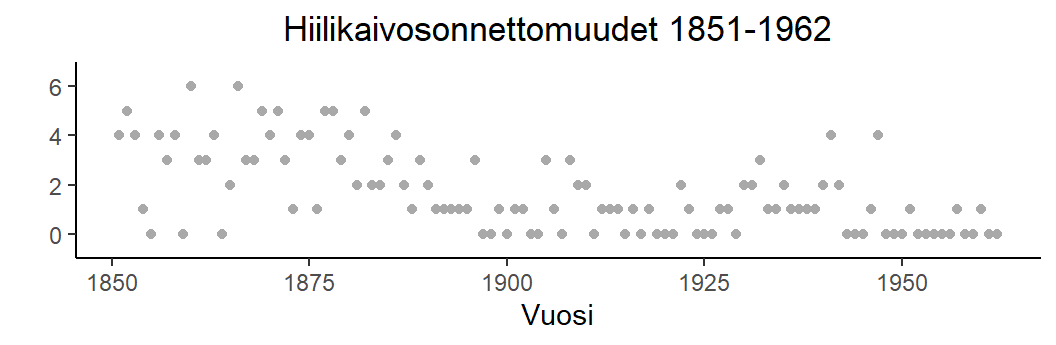
Havaitaan, että onnettomuuksien intensiteetti vuosina 1851–1882 on luokkaa 4 per vuosi, kun taas siitä eteenpäin tämä intensiteetti on hieman yli 1 per vuosi. Yksinkertainen malli on Poisson-malli, jossa intensiteetti muuttuu yhden kerran tarkastelujakson aikana. Muutoskohta pidetään tuntemattomana.
Uskottavuus. Olkoon \(\lambda\) intensiteetti muutospisteeseen \(k\) saakka ja \(\mu\) siitä alkaen. Oletetaan, että on olemassa täsmälleen yksi muutospiste. Silloin \(k \in \{1,\ldots,n-1\}\), missä \(n\) on havaintojen lukumäärä. Oletetaan edelleen, että \[ \begin{aligned} y_i|\lambda,\mu,k &\sim \textrm{Poisson}(\lambda),\quad i = 1,\ldots,k,\quad \textrm{vaihdannaisia, ja} \\ y_i|\lambda,\mu,k &\sim \textrm{Poisson}(\mu),\quad i = k+1,\ldots,n,\quad \textrm{vaihdannaisia}. \end{aligned} \] Lisäksi \(y_i\) ja \(y_j\), \(i \leq k, j > k\) ovat ehdollisesti riippumattomia ehdolla \(\lambda,\mu,k\).
Priorit. Asetetaan prioreiksi
\(\lambda \sim \textrm{Gamma}(A,B)\)
\(\mu \sim \textrm{Gamma}(C,D)\)
\(k \sim \operatorname{Tas}(\{1,\ldots,n-1\})\)
Parametrit \(\lambda, \mu\) ja \(k\) oletetaan lisäksi riippumattomiksi a priori. Valitaan heikosti informatiiviset priorit asettamalla \(A = C = 0.01\) ja \(B = D = 0.01\).
Posteriori. Edellä olevat valinnat johtavat normeeraamattomaan posterioriin \[ \begin{aligned} p(\lambda,\mu,k|y) &\propto p(k)p(\lambda)p(\mu)p(y|\lambda,\mu,k) \\ &\propto \lambda^{A+\sum_{i=1}^k y_i - 1}\mu^{C + \sum_{j=k+1}^n y_j-1} e^{-[(B+k)\lambda + (D + (n-k))\mu]}. \end{aligned} \]
Posteriorin simulointi MCMC-menetelmällä. Suoraviivaisin algoritmi on komponenteittain tapahtuva päivittäminen, jossa yhdellä kierroksella päivitetään
\(\lambda\) Gibbsin algoritmilla
\(\mu\) edelleen Gibbsin algoritmilla
\(k\) Metropolisin algoritmilla.
Kyseessä on ns. “Metropolis within Gibbs” -lähestymistapa. Gibbsin algoritmia käytetään päivityksissä silloin, kun parametrien ehdolliset jakaumat ovat helposti laskettavissa. Muulloin käytetään Metropolisin päivitystä.
Toimitaan siis seuraavasti: \[ (\lambda,\mu,k) \rightarrow (\lambda^*,\mu,k) \rightarrow (\lambda^*,\mu^*,k) \rightarrow (\lambda^*,\mu^*,k^*). \]
1. \(\boldsymbol{\lambda}\) :n päivitys
Lasketaan ehdollinen jakauma \(p(\lambda|\mu,k,y)\) \[ p(\lambda|\mu,k,y) \propto \lambda^{A + \sum_{i=1}^k y_i - 1}e^{-(B+k)\lambda}, \] joka on \(\textrm{Gamma}(A + \sum_{i=1}^k y_i, B + k)\).
2. \(\boldsymbol{\mu}\) :n päivitys
Lasketaan ehdollinen jakauma \(p(\mu|\lambda,k,y)\) \[ p(\mu|\lambda,k,y) \propto \lambda^{C + \sum_{j=k+1}^n y_j - 1}e^{-[D+(n-k)]\lambda}, \] joka on \(\textrm{Gamma}(C + \sum_{j=k+1}^n y_j, D+(n-k))\).
3. \(\boldsymbol{k}\) :n päivitys
Tässä ei ole mahdollista päätyä yksinkertaiseen ehdolliseen jakaumaan \(p(k|\lambda,\mu,y)\). Päädytään suosiolla Metropolis-Hastings -menetelmään. Ensin on päätettävä ehdotusjakauma, jonka arvojoukko on \(\{1,\ldots,n-1\}\). Pyritään symmetriseen ehdotusjakaumaan (vaikka se ei olekaan tarpeen) yhdistämällä aika-akselin ensimmäinen ja viimeinen arvo: \[ q(k,k^*) = \begin{cases} \frac13 & \text{kun } k = k^*, \\ \frac13 & \text{kun } |k - k^*| = 1, \\ 0 & \text{muutoin}, \end{cases} \] mutta kuitenkin siten, että \[ \begin{aligned} q((n-1),1) &= \frac13 \\ q(1,(n-1)) &= \frac13. \end{aligned} \] Hyväksymistodennäköisyys on \(\alpha = \min(1,r)\), missä \[ r = \lambda^{\sum_{i=1}^{k^*} y_i - \sum_{j=1}^k y_j} \mu^{\sum_{i=k^*+1}^n y_i - \sum_{j=k+1}^n y_j}e^{-(k^*-k)\lambda + (k^*-k)\mu}. \]
Implementointi
disaster_gibbs <- function(y, n_sim, n_burn, theta_0, A, B, C, D) {
n <- length(y)
# Tässä theta = (lambda, mu, k)
theta <- matrix(ncol = 3, nrow = n_sim + n_burn)
theta[1, ] <- theta_0
k <- theta[1, 3]
for (i in 2:(n_sim + n_burn)) {
lambda <- rgamma(1, A + sum(y[1:k]), rate = B + k)
mu <- rgamma(1, C + sum(y[(k + 1):n]), rate = D + (n - k))
k_star <- sample((k - 1):(k + 1), size = 1)
if (k_star == 0) {
k_star <- n - 1
}
else if (k_star == n) {
k_star <- 1
}
r <- lambda^(sum(y[1:k_star]) - sum(y[1:k])) *
mu^(sum(y[(k_star + 1):n]) - sum(y[(k + 1):n])) *
exp(-(k_star - k) * lambda + (k_star - k) * mu)
k <- ifelse(rbinom(1, size = 1, prob = min(1, r)), k_star, k)
theta[i,] <- c(lambda,mu,k)
}
theta[seq(n_burn + 1, n_burn + n_sim), ]
}
dis_res <- disaster_gibbs(hiili, 2e4, 1e4, c(4, 1, 40), 0.01, 0.01, 0.01, 0.01)
dis_res[, 3] <- dis_res[, 3] + 1850 # muunnetaan erotus vuodesta 1850 vuosiluvuksiSimuloinnin tuloksena saadaan seuraavat tunnusluvut parametreille \(\lambda, \mu\) ja \(k\)
| Mean | SD | 2.5 % | 97.5 % | |
|---|---|---|---|---|
| \(\lambda\) | 3.1433664 | 0.2963688 | 2.5922771 | 3.750606 |
| \(\mu\) | 0.8944891 | 0.1140621 | 0.6826878 | 1.128793 |
| \(k\) | 1889.1203000 | 2.2369797 | 1886.0000000 | 1895.000000 |
Muutospisteen \(k\) posterioritodennäköisyysjakauma on

Parametrien otospolut ovat
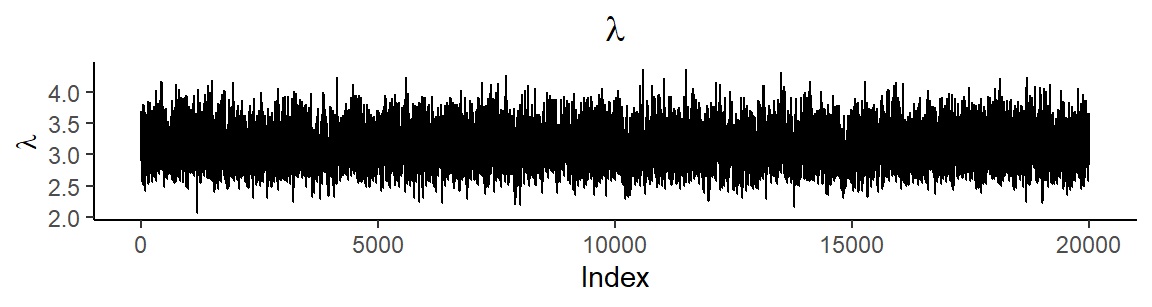
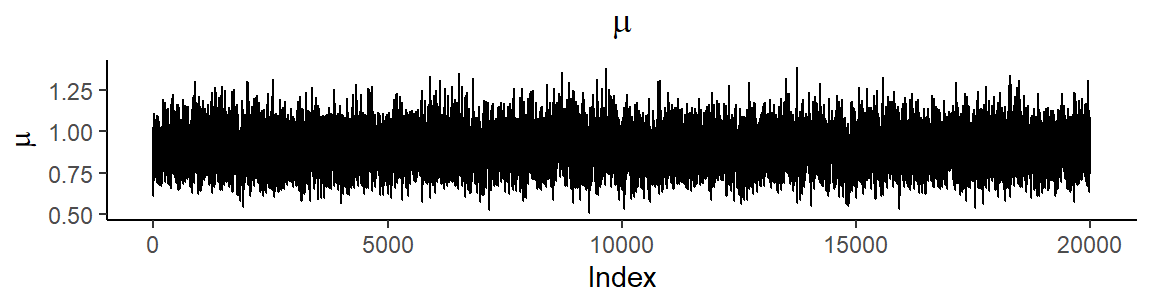
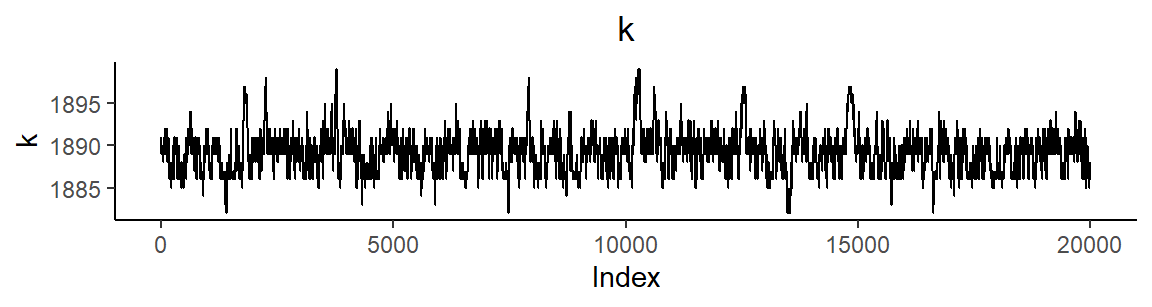
Onnettomuusintensiteetin estimointi Stanilla
Edellistä mallia ei voi suoraan estimoida Stanilla, koska muutospisteparametri \(k\) saa diskreettejä arvoja. Myös suora parametrin \(k\) tulkitseminen reaaliarvoiseksi on ongelmallista, koska posterioritiheys riippuu \(k\):n arvosta epäjatkuvasti. Sen sijaan voidaan määritellä lähes vastaava malli, missä onnettomuuksien määrää kuvaavan Poisson-jakautuneen muuttujan parametri riippuu jatkuvasti vuodesta ja parametrista \(k\). Olkoon \(y_i\) vuonna \(t_i\) tapahtuneiden hiilikaivosonnettomuuksien lukumäärä. Määritellään malli \[ y_i \sim \textrm{Poisson}\left(\lambda + (\mu-\lambda) f\left(\frac{t_i-k}{\sigma} \right)\right), \] missä \(f(x)\) on sopiva jatkuva funktio, jolla \(f(x) \approx 0\) kun \(x \ll 0\) ja \(f(x) \approx 1\) kun \(x \gg 0\); valitaan tässä \[ f(x) = \frac{1}{1 + e^{-x}} \] eli käänteinen logit-muunnos. Parametreilla \(\lambda\), \(\mu\) ja \(k\) on sama tulkinta kuin edellä. Niiden lisäksi mallissa on mukana onnettomuusintensiteetin muutoksen nopeutta kuvaava parametri \(\sigma\), jonka pienet arvot tarkoittavat jyrkkää muutosta. Valitsemalla heikosti informatiivisia prioreja parametreille päädytään malliin \[ \begin{aligned} y_i|\lambda, \mu, k, \sigma & \sim \textrm{Poisson}\left(\lambda + (\mu-\lambda) f\left(\frac{t_i-k}{\sigma} \right)\right) \\ \lambda & \sim \mathrm{Puoli-}\operatorname{N}(0, 10^2) \\ \mu & \sim \mathrm{Puoli-}\operatorname{N}(0, 10^2) \\ k & \sim \operatorname{Tas}(1851, 1962) \\ \sigma & \sim \mathrm{Puoli-}\operatorname{N}(0, 2^2). \end{aligned} \] Jyrkkyysparametrille \(\sigma\) on annettu informatiivisempi, pieniä arvoja suosiva priori. Stanilla malli toteutetaan seuraavasti.
scode <- "
data {
int<lower=0> n; // vuosien määrä
int<lower=0> y[n]; // onnettomuuksien määrä
vector[n] year; // vuosi
}
parameters {
real<lower=min(year), upper=max(year)> k;
real<lower=0> lambda;
real<lower=0> mu;
real<lower=0> sigma;
}
model {
sigma ~ normal(0, 2);
lambda ~ normal(0, 10);
mu ~ normal(0, 10);
y ~ poisson(lambda + (mu - lambda) * inv_logit((year - k) / sigma));
}
"
n <- length(hiili)
fit <- stan(
model_code = scode,
data = list(n = n, y = hiili, year = 1851:1962),
iter = 3000,
warmup = 2000,
control = list(adapt_delta = 0.95),
verbose = FALSE
)Stan-mallin estimointi tuottaa seuraavat tunnusluvut
| Mean | SD | 2.5 % | 97.5 % | |
|---|---|---|---|---|
| \(k\) | 1888.6350030 | 2.3834612 | 1883.8597233 | 1893.314430 |
| \(\lambda\) | 3.2859154 | 0.3189696 | 2.7155102 | 3.955503 |
| \(\mu\) | 0.8786431 | 0.1159544 | 0.6602878 | 1.114393 |
| \(\sigma\) | 1.9350537 | 1.1374283 | 0.1742835 | 4.432952 |
Huomataan, että tulokset pitkälti vastaavat aikaisemmin saatuja. Muutospisteen \(k\) posterioritodennäköisyysjakauma tässä mallissa on

Keskiarvoistaminen
Analyysissa voidaan mennä vielä pidemmälle: lasketaan intensiteettifunktio ajan funktiona ja sille rajat (envelopes). Rajat kuvaavat väliä, jossa käyrä on suurella posterioritodennäköisyydellä. Tämä on alkeellinen esimerkki epäparametrisesta mallista, jossa yksinkertaista funktiota sovitetaan aineistoon suuri määrä ja niistä lasketaan keskiarvo sekä rajat.
Määritellään funktio, joka laskee intensiteetille minimit, maksimit sekä keskiarvon kullekin vuodelle
profile <- function(x) {
res <- t(sapply(1:ncol(x), function(i) {
c(
mean = mean(x[, i]),
min = min(x[, i]),
max = max(x[, i]),
year = 1850 + i
)
}))
as.data.frame(res)
}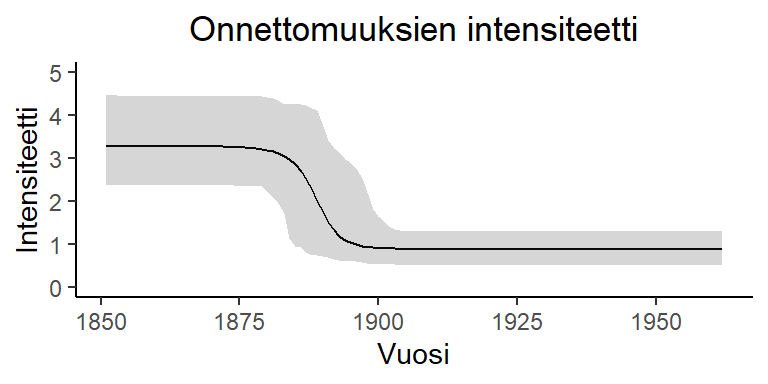
Intensiteetin mallinnuksessa voitaisiin mennä pidemmälle ja käyttää joustavampia parametrisiä funktioperheitä. Olisi esimerkiksi suoraviivaista käyttää useampaa kuin yhtä muutospistettä, tai lineaarista mallia log-intensiteetille. Vieläkin joustavampia funktioperheitä saataisiin sovitettua epäparametrisilla malleilla. Voitaisiin esimerkiksi määritellä, että onnettomuuksien log-intensiteetti eri vuosina on gaussinen vektori, jolla on epätriviaali kovarianssimatriisi eli log-intensiteetti mallinnettaisiin gaussisena prosessina.
5.3 Nollapaisutettu Poisson-jakauma
Tarkastellaan tilannetta, jossa muuttuja saa ei-negatiivisia kokonaislukuarvoja \(\{0,1,2,\ldots\}\). Perusteltu malli “harvinaisille riippumattomille tapahtumille” on \(\textrm{Poisson}(\mu)\) -jakauma.
Usein Poisson-malli ei ole sellaisenaan sopiva syystä, että arvo \(0\) esiintyy useammin kuin jakauma edellyttää. Esimerkkinä olkoon astmakohtaukset annetulla aikavälillä: On niitä, jotka voivat saada allergiakohtauksen ja kohtausten määrä on Poisson-jakautunut, kun taas osa henkilöistä ei voi saada kohtausta lainkaan (ovat täysin terveitä). Kuitenkaan aineiston keruussa tätä erottelua ei voida tehdä. Komplikaationa on, että aineistossa on kahdenlaisia nollia: sellaisia, jotka eivät ole saaneet kohtausta (mutta voisivat saada) ja sellaisia, jotka eivät edes voi saada kohtausta (rakenteellisia nollia).
Tällaiseen tilanteeseen on ehdotettu nollapaisutettua Poisson-jakaumaa (Zero-inflated Poisson Distribution, ZIP): \[ p(k|\mu, \omega) = \begin{cases} (1 - \omega) + \omega e^{-\mu} & \text{kun } k = 0, \\ \omega\frac{\mu^k e^{-\mu}}{k!} & \text{kun } k \geq 1. \end{cases} \] Tässä parametrisoinnissa \(\omega\) on todennäköisyys sille, että henkilö kuuluu siihen populaation osaan, joka voi sairastua. Tämä jakauma on seos jakaumista \(\textrm{Poisson}(\mu)\) ja \(\textrm{Poisson}(0)\).
Esimerkki 5.4 (Astmakohtaukset) On annettu aineisto (astmakohtausten lukumäärä viimeisen kuukauden aikana) sadalta tutkimukseen osallistuneelta. Voidaan olettaa, että havainnot ovat vaihdannaisia (asthma.dat).
Havaitaan, että aineiston keskiarvo on \(0.74\) ja varianssi \(1.2448\), joten aineistossa on ylihajontaa.
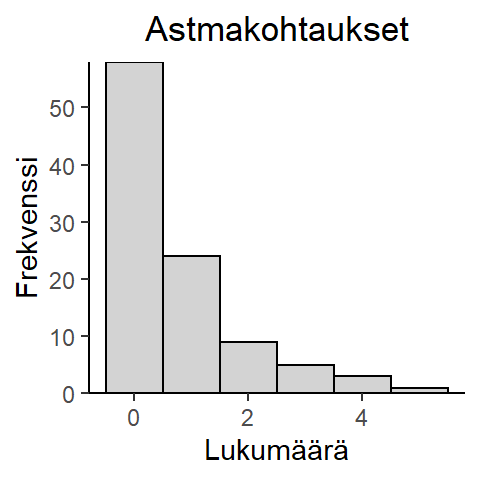
Sovitetaan nollapaisutettu Poisson-jakaumamalli tähän aineistoon Stania käyttäen.
Oletetaan, että otosyksiköille \(i\), joille on mahdollista, että \(y_i > 0\): \[ \begin{aligned} y_i|\mu &\sim \textrm{Poisson}(\mu) \\ \mu &\sim \textrm{Gamma}(0.5, 0.01) \end{aligned} \] Näiden otosyksiköiden osuus populaatiossa on \(\omega\), jolle asetetaan \[ \omega \sim \operatorname{Tas}(0,1). \] Uskottavuusfunktio voidaan siis kirjoittaa muodossa \[ p(y_i|\mu, \omega) = \begin{cases} (1 - \omega) + \omega e^{-\mu} & \text{kun } y_i = 0, \\ \omega\frac{\mu^{y_i} e^{-\mu}}{y_i!} & \text{kun } y_i \geq 1, \end{cases} \] joka voidaan implementoida suoraan Stanissa.
scode <- "
data {
int<lower=0> n; // koehenkilöiden lukumäärä
int y[n]; // astmakohtausten määrä
}
parameters {
real<lower=0, upper=1> omega;
real<lower=0> mu;
}
model {
mu ~ gamma(0.5, 0.01);
for (i in 1:n) {
if (y[i] > 0) target += log(omega) + poisson_lpmf(y[i] | mu);
else target += log((1-omega) + omega*exp(-mu));
}
}
"
n <- length(astma)
fit <- stan(
model_code = scode,
data = list(n = n, y = astma),
iter = 2000,
verbose = FALSE
)Simuloinnin tuloksena saadaan:
| Mean | SD | 2.5 % | 97.5 % | |
|---|---|---|---|---|
| \(\mu\) | 1.2497894 | 0.2048896 | 0.8820757 | 1.6825948 |
| \(\omega\) | 0.5999699 | 0.0866487 | 0.4415136 | 0.7807039 |
Parametrien otospolut yhdessä ketjussa ovat
Marginaaliposteriorit ovat


Voidaan sanoa, että sairastavien ryhmässä intensiteetin 95 %:n posterioriväli on (0.88, 1.68) ja populaatiosta 60 % kuuluu tähän ryhmään. Jälkimmäinen arvio on melko epätarkka: sen 95 %:n posterioriväli on (0.44, 0.78).
5.4 Moniulotteiset vasteet
Oletetaan, jokaiselta yksilöltä on saatu on \(m\) mittausta. Olkoot indeksi \(i = 1,\ldots,n\), joka liittyy yksilöön, ja \(j = 1,\ldots,m\), joka liittyy havaintoon. Tällöin \(y_{ij}\) on yksilöltä \(i\) saatu mittaus \(j\). Mikäli mittaukset saavat arvoja reaaliakselilta, voi normaalijakauma olla varteenotettava vaihtoehto havaintojen malliksi. Koska samalta yksilöltä tehdyt mittaukset ovat mahdollisesti korreloituneita, niin oletetaan että ne noudattavat moniulotteista normaalijakaumaa, missä odotusarvovektori \(\mu\) ja kovarianssimatriisi \(\Sigma\) ovat tuntemattomia: \[ y_i = (y_{i1},\ldots,y_{im})^T|\mu,\Sigma \sim \textrm{N}_m(\mu, \Sigma),\quad i = 1,\ldots,n. \] Jos on lisäksi havaittu joukko kovariaatteja, kuten ikä mittaushetkellä, voidaan odotusarvon \(\mu\) komponentteja kuvata monimuuttujaisella lineaarisella regressiomallilla: \[ \mu_j = \beta_0 + \sum_{k=1}^p \beta_k x_{kj}, \quad j = 1,\ldots,m, \] missä \(x_{kj}\) on \(j\):s kovariaatin \(k\) arvo. Tyypillisesti regressiokertoimille \(\beta\) oletetetaan epäinformatiiviset normaalijakaumapriorit ja kovarianssimatriisille oletetaan käänteinen Wishart-jakauma, jolloin \(\Sigma^{-1} \sim \textrm{Wishart}(R, \rho)\) (Wishart-jakauma on moniulotteisen normaalijakauman käänteisen kovarianssimatriisin konjugaattipriori). Tässä \(R\) on niin sanottu “skaalamatriisi” ja \(\rho\) on jakauman vapausasteiden lukumäärä. Wishart-jakauma voidaan mieltää khiin-neliö -jakauman moniulotteiseksi yleistykseksi, joka ilmaantuu klassisessa tilastotieteessä neliösummien ja -tulojen matriisin jakaumana moniulotteisesta normaalijakaumasta tehdyn otannan yhteydessä. Odotusarvovektoriin \(\mu\) voidaan liittää muunkinlaisia parametrisointeja, mikäli mittaukset \(y_{ij}\) eivät esimerkiksi ole mittauksia samasta vasteesta eri ajanhetkillä vaan mittauksia eri vasteista samalla ajanhetkellä. Mikäli mitatut vasteet muuttuvat ajassa, on myös mahdollista tarkastella ajassa muuttuvia kovariaatteja.
Vähiten informatiivinen aito Wishart-priori saadaan asettamalla \(\rho = r\), missä \(r\) on jakauman dimensio (tyypillisesti \(r = m\)). Prioriodotusarvo on \(\rho R^{-1}\), jolloin hyvä valinta matriisiksi \(R\) on \(\rho\Sigma_0\), missä \(\Sigma_0\) on jokin ennakkoarvaus kovarianssimatriisiksi.
Monimuuttujainen lineaarinen regressio voidaan helposti yleistää epälineaarisiin regressionmalleihin, aivan kuten yksiulotteisessa tapauksessa. Virhetermeille voidaan määrittää moniulotteinen \(t\)-jakauma poikkeavia havaintoyksiköitä varten. Priorijaukaumien valinta ei kuitenkaan ole aivan yhtä suoraviivaista. Kovarianssimatriisin tulee olla positiivisesti definiitti, ja Wishart-jakauma on ainoa tyypillisesti käytetty jakauma, joka toteuttaa tämän rajoitteen luonnollisella tavalla. (Tosin esim. Stanissa on implementoitu Lewandowski–Kurowicka–Joe-jakauma (LKJ) korrelaatiomatriiseille, jonka pohjalta voidaan rakentaa prioreja kovarianssimatriiseille.) Jos halutaan käyttää priorijakaumaa, jossa tämä kovarianssimatriisia koskeva rajoite ei suoraan toteudu, on se otettava mallissa huomioon muilla keinoin.
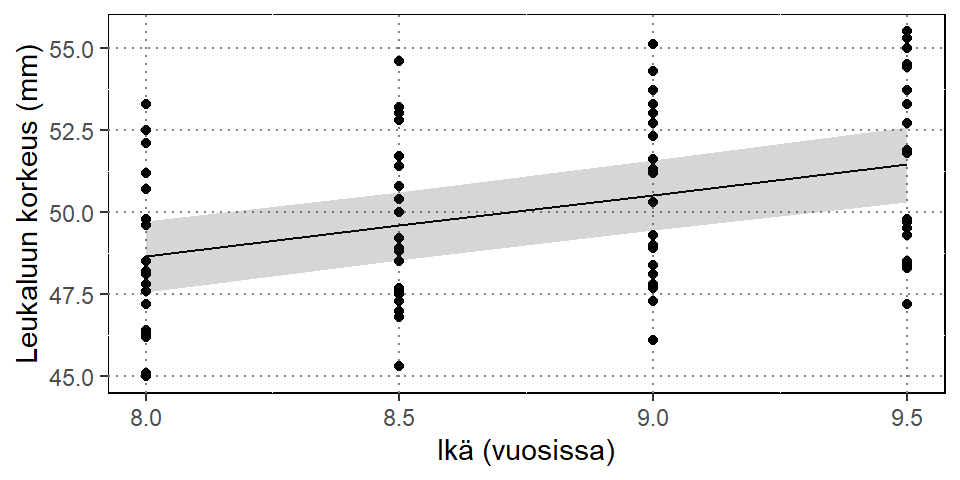
Esimerkki 5.5 (Leukaluut) Elston ja Grizzle (1962) esittävät aineiston, jossa 20 pojalta on mitattu leukaluun korkeudet 8, 8.5, 9 ja 9.5 vuosien iässä. Tarkoituksena on mallintaa keskimääräistä kasvukäyrää.
Yksinkertainen lineaarinen malli voidaan sovittaa Stanilla seuraavasti:
scode <- "
data {
int<lower=0> n; // mittausten lukumäärä
int<lower=0> m; // kovariaattien määrä
vector[m] y[n]; // mittaukset
vector[m] x; // kovariaatit
}
parameters {
real beta[2];
cov_matrix[m] Sigma;
}
transformed parameters {
vector[m] mu;
mu = beta[1] + beta[2]*x;
}
model {
Sigma ~ inv_wishart(m, diag_matrix(rep_vector(1, m)));
y ~ multi_normal(mu, Sigma);
}
"
fit <- stan(
model_code = scode,
data = list(n = nrow(jaws), m = ncol(jaws), y = jaws, x = c(8, 8.5, 9, 9.5)),
iter = 2000,
verbose = FALSE
)Simuloinnin tuloksena saadaan:
| Mean | SD | 2.5 % | 97.5 % | |
|---|---|---|---|---|
| \(\beta_0\) | 33.783375 | 1.9333220 | 29.981333 | 37.569387 |
| \(\beta_1\) | 1.860502 | 0.2190931 | 1.422629 | 2.288065 |
| \(\mu_1\) | 48.667391 | 0.5463749 | 47.552054 | 49.715197 |
| \(\mu_2\) | 49.597642 | 0.5362674 | 48.523626 | 50.618806 |
| \(\mu_3\) | 50.527893 | 0.5483072 | 49.439206 | 51.574860 |
| \(\mu_4\) | 51.458144 | 0.5811194 | 50.296197 | 52.594412 |
Kuviossa ovat alkuperäiset havainnot, keskiarvosovite sekä 95 % posterioriväli.
5.5 Regularisointi
Tarkastellaan lineaarista regressiomallia \[ y = X\beta + \epsilon, \] missä \[ y = \begin{pmatrix} y_1 \\ \vdots \\ y_n \end{pmatrix},\, X = \begin{pmatrix} x_{11} & x_{12} & \cdots & x_{1m} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{2n} & \cdots & x_{nm} \end{pmatrix}, \] \[ \beta = \begin{pmatrix} \beta_1 \\ \vdots \\ \beta_m \end{pmatrix},\, \epsilon = \begin{pmatrix} \epsilon_1 \\ \vdots \\ \epsilon_n \end{pmatrix}. \] Tällöin PNS-ratkaisun estimointiyhtälöt ovat (Gauss-Markovin lauseen nojalla) \[ X^\top X\beta = X^\top y. \] Tämän yhtälön ratkaisu \(\hat\beta = (X^\top X)^{-1}X^\top y\) edellyttää, että matriisi \(X^\top X\) on täysiasteinen, jolloin käänteismatriisi \((X^\top X)^{-1}\) on olemassa.
On tilanteita, joissa matriisi \(X^\top X\) on “lähes” singulaarinen, esimerkiksi silloin, kun matriisin \(X\) sarakkeissa on (yksi tai useampi) vahvasti korreloiva muuttujapari. Tämä aiheuttaa ongelmia estimoinnissa.
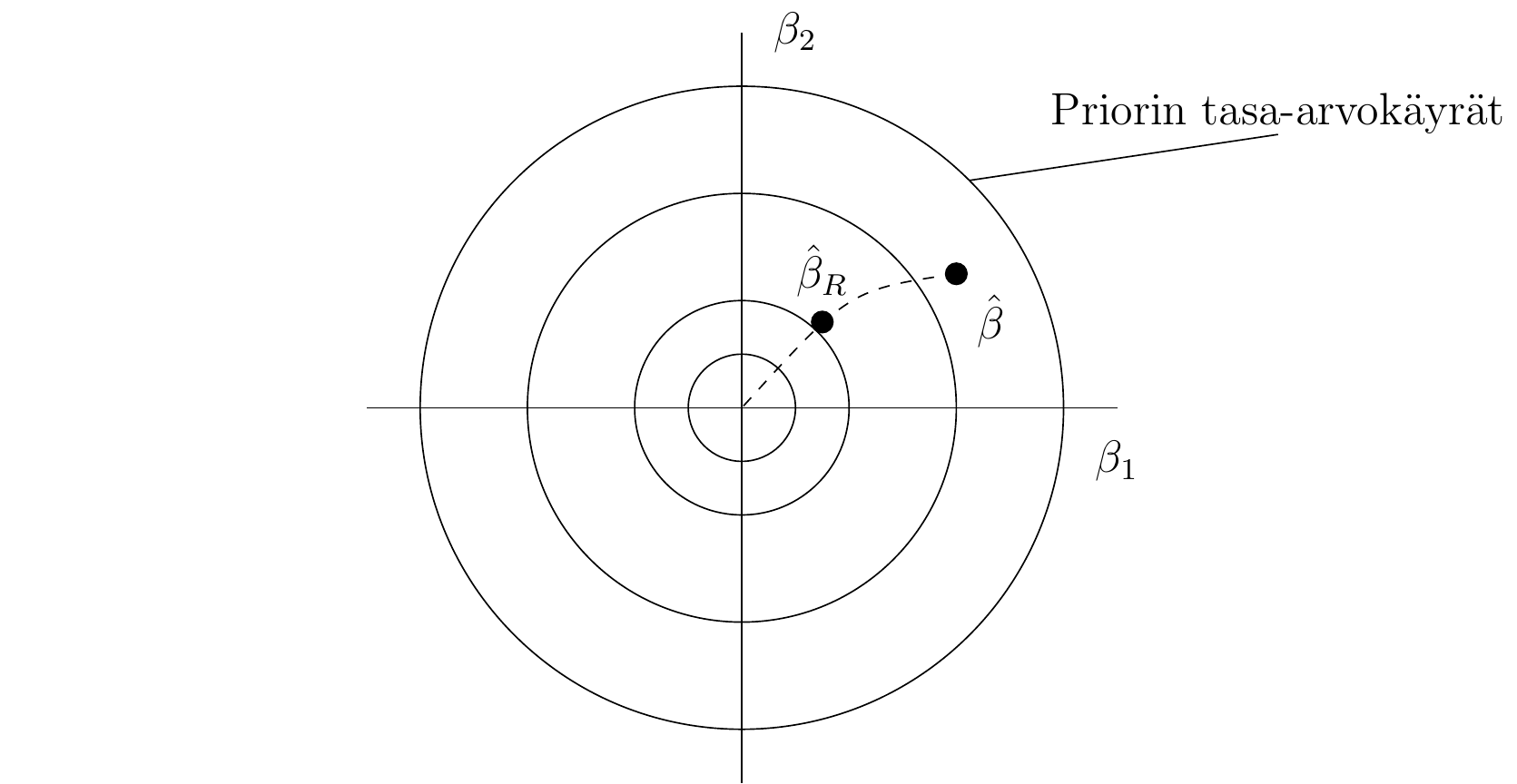
Yksi ratkaisu ongelmaan on ridge-regressio (harjanneregressio), jossa matriisi \(X^\top X\) regularisoidaan lisäämällä sen diagonaalille positiivisia alkioita. Ridge-estimaattori on \[ \hat{\beta}_R = (X^\top X + \lambda I)^{-1}X^\top y. \] Tämä estimaattori on harhainen, mutta estimaattorin komponenteilla voi olla pienemmät keskivirheet kuin PNS-estimaattorin komponenteilla.
Ridge-regressiolle voidaan löytää bayesiläinen formulointi, joka auttaa tulkinnassa.
Ridge-regression Bayes-formulointi. Oletetaan, että varianssi \(1/\tau\) on tunnettu. Tällöin \[ p(y|\beta) \propto \exp\left\{-\frac12 \tau (y - X\beta)^\top (y- X\beta)\right\}. \] Asetetaan prioriksi: \[ p(\beta) = \left(\frac{\kappa}{2\pi} \right)^{-M/2}\exp\left\{-\frac12\kappa\beta^\top\beta\right\}, \] eli siis \(\beta \sim \operatorname{N}_m(0, I/\kappa)\), missä \(\kappa\) on tunnettu vakio. Tällöin \[ \log p(\beta|y) \propto -\frac12 \left[\tau(y-X\beta)^\top(y-X\beta) + \kappa\beta^\top\beta \right]. \] Derivoimalla edellinen lauseke vektorin \(\beta\) komponenttien suhteen saadaan \[ \dfrac{\partial \log p}{\partial \beta} = \tau X^\top y - \tau X^\top X\beta - \kappa\beta. \] Asettamalla derivaatta nollaksi saamme yhtälön \[ (X^\top X + \dfrac{\kappa}{\tau}I)\beta = X^\top y, \] jonka ratkaisu on \[ \overline \beta = (X^\top X + \lambda I)^{-1}X^\top y,\, \textrm{missä } \lambda = \dfrac{\kappa}{\tau}. \] Posteriori on \(m\)-ulotteinen normaalijakauma ja sen moodi (ja myös odotusarvo) on \(\overline \beta\).
Tulos: Harjanne-estimaattori on posterioriodotusarvo silloin, kun priori on \(\beta \sim \operatorname{N}(0, I/\kappa), \kappa = \lambda\tau.\)
Priorilla on “kutistava” vaikutus:
5.6 Puuttuva tieto
Lähes kaikki käytännön aineistot sisältävät puuttuvaa tietoa. Havaintoyksiköltä voi esimerkiksi puuttua joidenkin muuttujien arvoja, tai havaintoyksikkö voi puuttua kokonaan. Puuttuvaa tietoa syntyy myös sensuroinnin seurauksena.
Oletetaan, että data on \(y\). Se jaetaan kahteen osaan, havaittuun dataan \(y^\textrm{obs}\) ja puuttuvaan tietoon \(y^\textrm{mis}\), eli \(y = (y^\textrm{obs},y^\textrm{mis})\). Klassisessa tilastotieteessä käytetään pääasiassa neljää tapaa puuttuvan tiedon käsittelyssä:
Puuttuva tieto jätetään pois (naiivi menetelmä).
Puuttuva tieto imputoidaan yksinkertaisesti, esim. keskiarvolla.
Käytetään moni-imputointia (Rubin).
Mallinnetaan puuttuvuusmekanismi ja sovelletaan EM-algoritmia (Expectation Maximization) tai jotain muuta menetelmää.
Näistä vaihtoehto (1) johtaa lähes aina virheellisiin päätelmiin, mutta voi toimia joissain harvoissa erikoistapauksissa, vaihtoehto (2) vähintäänkin aliarvioi todellista vaihtelua, (3) on monipuolinen vaihtoehto, mutta voi olla usein hankala toteuttaa käytännössä ja (4) sopii suurimman uskottavuuden lähestymistavan yhteyteen ja toimii oikein.
Periaatetasolla puuttuvan tiedon käsittely Bayes-lähestymistavassa on varsin yksinkertaista. Puuttuva tieto \(y^\textrm{mis}\) voidaan ajatella tuntemattomaksi parametriksi, aivan kuten mallin parametrit \(\theta\) tai muut havaitsemattomat suureet. Siksi on luonnollista pyrkiä konstruoimaan posteriori \[ p(\theta, y^\textrm{mis}|y^\textrm{obs}). \] Silloin parametrien \(\theta\) marginaaliposteriori on \[ p(\theta|y^\textrm{obs}) = \int p(\theta, y^\textrm{mis}|y^\textrm{obs})\, dy^\textrm{mis}. \] MCMC-menetelmillä posteriori saadaan tietysti käsittelemällä vain \(\theta\):sta tehtyjä simulointeja. Posteriori \(p(\theta, y^\textrm{mis}|y^\textrm{obs})\) on kuitenkin simuloitava!
Sivutuotteena puuttuvasta tiedosta saadaan informaatiota marginaaliposteriorijakauman \(p(y^\textrm{mis}|y^\textrm{obs})\) kautta, sillä siihen liittyvä epävarmuus tiedetään.
Oletetaan, että täydellinen aineisto on \[ y = (y_1,\ldots,y_n), \] ja mallina on \(p(y|\theta)\). Otetaan käyttöön indikaattorifunktio \[ I = (I_1,\ldots,I_n), \] missä \[ I_i = \begin{cases} 1 & \text{jos } y_i \text{ havaitaan,} \\ 0 & \text{muuten.} \end{cases} \] Esimerkiksi jos \(y_1, y_2, y_5, y_6\) ovat havaitut (aikasarjan) arvot ja havainnot \(y_3, y_4\) ovat puuttuvia, niin silloin: \[ \begin{aligned} \textrm{Täydellinen aineisto: }& y_1,\ldots,y_6 \\ \textrm{Havaittu aineisto: }& y_1,y_2,y_5,y_6 \text{ ja } I = (1,1,0,0,1,1). \end{aligned} \] Oletetaan edelleen, että \[ p(y,I|\theta,\phi) = p(y|\theta)p(I|y,\phi), \] missä oikean puolen ensimmäinen termi on täydellisen aineiston uskottavuus. Toinen termi on puuttuvuuden malli ja \(\phi\) sisältää siihen liittyvät parametrit. Oletetaan siis, että puuttuminen ei riipu parametreista \(\theta\).
Lisäksi oletetaan, että jokainen \(I_i, i = 1,\ldots,n\) havaitaan. Tällöin havaittujen suureiden uskottavuus on \[ p(y^\textrm{obs},I|\theta,\phi) = \int p(y^\textrm{obs},y^\textrm{mis}|\theta)p(I|y^\textrm{obs},y^\textrm{mis},\phi)\, dy^\textrm{mis}. \] Puuttuvien havaintojen luonne määrä sen, minkälainen uskottavuus lopulta on.
Vaikka puuttuvan tiedon käsittely Bayes-tilastotieteessä on ajatuksellisesti yksinkertaista, ei se ole välttämättä sitä käytännössä. Puuttuvuudesta täytyy olla tietoa, jotta puuttuvuusmekanismi voidaan mallintaa.
Rubin (1987) määrittelee kolme puuttumisen muotoa:
Täysin satunnainen puuttuminen (Missing Completely At Random, MCAR, ), jos \[ p(I|y^\textrm{obs},y^\textrm{mis},\phi) = p(I|\phi).\]
Satunnainen puuttuminen (Missing At Random, MAR), jos \[ p(I|y^\textrm{obs},y^\textrm{mis},\phi) = p(I|y^\textrm{obs},\phi).\]
Ei-satunnainen (informatiivinen) puuttuminen (Missing Not At Random, MNAR), jos \(p(I|y^\textrm{obs},y^\textrm{mis},\phi)\) riippuu sekä havaitusta aineistosta \(y^\textrm{obs}\) että puuttuvasta aineistosta \(y^\textrm{mis}\).
Satunnaisen puuttumisen (MAR) tapauksessa uskottavuus on \[ \begin{aligned} p(y^\textrm{obs},I|\theta,\phi) &= \int p(y^\textrm{obs},y^\textrm{mis}|\theta)p(I|y^\textrm{obs},y^\textrm{mis},\phi)\, dy^\textrm{mis}\\ &= p(I|y^\textrm{obs},\phi) \int p(y^\textrm{obs},y^\textrm{mis}|\theta)\, dy^\textrm{mis}\\ &= p(I|y^\textrm{obs},\phi) p(y^\textrm{obs}|\theta). \end{aligned} \] Jos oletetaan, että \(p(\theta,\phi) = p(\theta)p(\phi)\), niin posteriori on silloin \[ \begin{aligned} p(\theta,\phi|y^\textrm{obs},I) &= \dfrac{p(\theta)p(\phi)p(y^\textrm{obs},I|\theta,\phi)}{\int p(\theta)p(\phi)p(y^\textrm{obs},I|\theta,\phi)\, d\theta d\phi} \\ &= \dfrac{p(\theta)p(y^\textrm{obs}|\theta)}{\int p(\theta)p(y^\textrm{obs}|\theta)\, d\theta} \dfrac{p(\phi)p(I|y^\textrm{obs},\phi)}{\int p(\phi)p(I|y^\textrm{obs},\phi)\, d\phi} \\ &= p(\theta|y^\textrm{obs}) p(\phi|I,y^\textrm{obs}). \end{aligned} \] Siten parametrien \(\theta\) marginaaliposteriori on \[ p(\theta|y^\textrm{obs},I) = p(\theta|y^\textrm{obs}) \int p(\phi|I,y^\textrm{obs})\, d\phi = p(\theta|y^\textrm{obs}). \] Seuraus: parametreja \(\theta\) koskeva Bayes-inferenssi perustuu posterioriin \[ p(\theta|y^\textrm{obs}) \propto p(\theta)p(y^\textrm{obs}|\theta). \] Sanotaan, että puuttuvuusmekanismi on epäoleellinen (ignorable). Käytännössä tämä merkitsee sitä, että puuttumista ei tässä tapauksessa tarvitse ottaa huomioon.
Posteriorin laskenta ja moni-imputointi
Posteriori on (yleisessä muodossa) \[ p(\theta, \phi, y^\textrm{mis}| y^\textrm{obs}). \] Sen simulointi MCMC-menetelmällä johtaa simuloituihin arvoihin \((\theta^{(t)},\phi^{(t)},{y^\textrm{mis}}^{(t)})\), \(t = 1,\ldots,T\), josta saadaan approksimaatio marginaaliposteriorille \(p(\theta|y^\textrm{obs})\) tarkastelemalla vain simuloitua jonoa \(\{\theta^{(t)}\}\). Puuttuvien arvojen \(y^\textrm{mis}\) laskemista simuloinneista \(\{{y^\textrm{mis}}^{(t)}\}\) sanotaan moni-imputoinniksi.
On syytä huomata imputoinnin ja moni-imputoinnin ero: Moni-imputoinnissa pyritään tuottamaan useita arvoja puuttuville havainnoille \(y^\textrm{mis}\). Tämä toteutuu Bayes-lähestymistavassa luonnollisella tavalla.
Esimerkki 5.6 (Sensurointi puuttuvana tietona) Oletetaan, että \(y_i|\theta \sim \operatorname{Exp}(\theta)\), \(i = 1,\ldots,n,\) ehdollisesti riippumattomia ehdolla \(\theta\). Havainto \(y_i\) puuttuu, jos \(y_i > y_0\). Tällöin \[ I_i = \begin{cases} 1 & \text{jos } y_i \leq y_0 \\ 0 & \text{jos } y_i > y_0. \end{cases} \] Täydellinen uskottavuus on \[ p(y|\theta) = \theta^n \exp(-\theta \sum_{i=1}^n y_i), \] kun taas havaittu uskottavuus on \[ p(y^\textrm{obs},I|\theta,y_0) = \prod_{i=1}^n\left[ p(y_i|\theta)^{I_i} P(y_i > y_0|\theta,y_0)^{1-I_i} \right]. \] Tästä voidaan päätellä, että \(p(I|y^\textrm{obs},y^\textrm{mis},y_0)\) riippuu puuttuvista havainnoista, joten otanta ei ole epäoleellinen.
Esimerkki 5.7 (Sensurointi puuttuvana tietona. (jatk.)) Oletetaan, että havainnointi lopetetaan, kun \(m_0 < n\) havaintoa on tehty, missä \(m_0\) ei riipu havainnoista \(y_i\). Oletetaan katkaisumäärä \(m_0\) tunnetuksi. Katkaisu on siis havaintosarjassa riippumatta havaintojen \(y_i\) arvoista. Tällöin \[ \begin{aligned} y^\textrm{obs}&= (y_1,\ldots,y_{m_0}) \\ y^\textrm{mis}&= (y_{m_0 + 1},\ldots,y_n). \end{aligned} \] Edelleen \(I_i = 1\), kun \(i = 1,\ldots,m_0\) ja \(I_i = 0\), kun \(i = m_0 + 1, \ldots, n\). Havaittuun tietoon perustuva uskottavuus on \[ p(y^\textrm{obs},I|\theta,m_0) = \prod_{i=1}^n p(y_i|\theta)^{I_i}. \] Tällöin \(p(I|y^\textrm{obs},y^\textrm{mis},m_0) = p(I|m_0)\). Kyseessä on täydellisesti satunnainen puuttuminen (MCAR).
Esimerkki 5.8 (Puuttuva suurin havainto) Oletetaan, että vaihdannaisista havainnoista \(y_1,\ldots,y_n\), \(y_{\textrm{max}} = \max\{y_1,\ldots,y_n\}\) puuttuu, ts. \(n-1\) havaintoarvoa on saatu ja tiedetään, että suurin havainto puuttuu. Minkälaisesta puuttumisesta on kyse? Pohdi, voidaanko tämä mallintaa!
5.7 Aikasarjamallinnus
Esimerkki 5.9 (AR-malli) Oletetaan, että \(y_0, y_1,\ldots,y_n\) on aikasarja, jolle \[ \begin{aligned} y_0|\sigma_0^2 &\sim \operatorname{N}(0,\sigma^2_0) \\ y_i|y_{i-1},\ldots,y_1,y_0,\alpha,\sigma^2 &\sim \operatorname{N}(\alpha y_{i-1},\sigma^2),\, i = 1,\ldots,n. \end{aligned} \] Tutumpi esitys on \[ y_i = \alpha y_{i-1} + \epsilon_i,\, i = 1,\ldots,n, \] missä \(\epsilon_i \sim \operatorname{N}(0,\sigma^2)\) ovat riippumattomia. Tämä on \(\textrm{AR}(1)\)-prosessi. Uskottavuusfunktio on muotoa \[ p(y|\alpha,\sigma^2) = p(y_0)\prod_{i=1}^n p(y_i|y_{i-1},\alpha,\sigma^2), \] kun oletetaan, että \(\sigma^2_0\) on tunnettu. Havainnot eivät ole vaihdannaisia.
Oletetaan nyt, että havainto \(y_i\) puuttuu riippumatta sen arvosta. Silloin \[ \begin{aligned} y^\textrm{obs}&= (y_0,\ldots,y_{i-1},y_{i+1},\ldots,y_n) = y_{-i} \\ y^\textrm{mis}&= y_i. \end{aligned} \] Tuntematon parametri on \(\theta = (\alpha,\sigma^2)\). Sille asetetaan priori \(p(\theta)\). Posteriori on \[ p(\theta,y^\textrm{mis}|y^\textrm{obs}) = p(\theta,y_i|y_{-i}). \] Simulointi on mahdollista (ja yksinkertaista) tehdä komponenteittain: Oletetaan, että on simuloitu \((\theta^{(k)},y_i^{(k)})\): \(y_i^{(k+1)}\) simuloidaan jakaumasta \(p(y_i|\theta^{(k)},y_{-i})\) ja tämän jälkeen \(\theta^{(k+1)}\) jakaumasta \(p(\theta|y_i^{(k+1)},y_{-i})\).
Huomaa, että \[
p(y_i|y_{-i}, \theta) = \dfrac{p(y_i|y_{i-1},\theta)p(y_{i+1}|y_i,\theta)}{\int p(y_i|y_{i-1},\theta)p(y_{i+1}|y_i,\theta)\, dy_i}
\] ja \[
p(\theta|y_{-i},y_i^{(k+1)})
\] on posteriori parametrille \(\theta\) ehdolla data, jossa puuttuva arvo \(y_i\) on korvattu edellisen päivityksen antamalla arvolla. Ensimmäinen askel on helppo tehdä lasketusta jakaumasta, toisen voi tehdä Metropolisin algoritmilla. NIMBLEssä riittää korvata puuttuva havainto NA:lla.
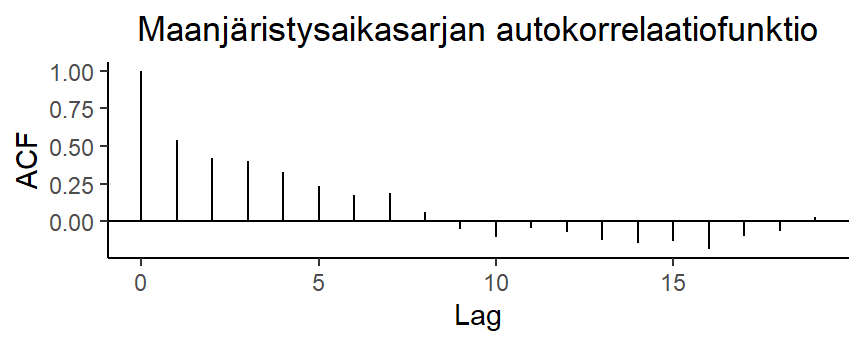
Esimerkki 5.10 (Maanjäristykset) Seuraava aineisto esittää vuosihavaintona 7.0 Richterin ylittävien maanjäristysten lukumäärää vuosilta 1900-1998 (99 havaintoa, earthq.dat).
Aineiston kuvaaja ja autokorrelaatiofunktio ovat:
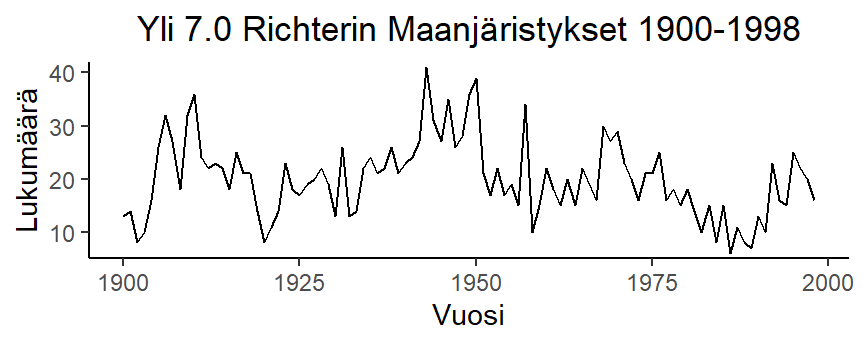
Aikasarjaa voidaan mallintaa gaussisena \(\textrm{AR}(1)\)-prosessina \[ y_i - m = \alpha(y_{i-1} - m) + \epsilon_i,\, i = 1,\ldots,n, \] missä \(m\) on aikasarjan odotusarvo. Suoritetaan Bayes-mallinnus tälle aikasarjalle seuraavin oletuksin:
Odotusarvo \(m\) estimoidaan aineistosta \[ \hat m = \frac{1}{n}\sum_{i=1}^n y_i, \] ja \[ \begin{aligned} y_1 &\sim \operatorname{N}(\hat m, 1/0.03) \\ y_i|\alpha,\tau,y_{i-1} &\sim \operatorname{N}(\hat m + \alpha(y_{i-1} -\hat m), 1/\tau),\, i = 2,\ldots,n \\ \alpha &\sim \operatorname{N}(0.5, 1/5) \\ \tau &\sim \textrm{Gamma}(0.3, 1), \end{aligned} \] missä \(\tau = 1/\sigma^2\). Mallin Stan-koodi on
scode <- "
data {
int<lower=0> n; // vuosien lukumäärä
real y[n]; // havainnot
real m_hat; // prosessin keskiarvo
}
parameters {
real alpha;
real<lower=0> tau;
}
transformed parameters {
real<lower=0> sigma;
sigma = 1 / sqrt(tau);
}
model {
alpha ~ normal(0.5, 1 / sqrt(5));
tau ~ gamma(0.3, 1);
y[1] ~ normal(m_hat, 1 / sqrt(0.03));
for (i in 2:n) {
y[i] ~ normal(m_hat + alpha * (y[i - 1] - m_hat), sigma);
}
}
"
fit <- stan(
model_code = scode,
data = list(n = length(earthq), m_hat = mean(earthq), y = earthq),
iter = 2000,
verbose = FALSE
)Posteriorijakauman kuvaus marginaaliposteriorien tunnusten avulla on seuraava:
| Mean | SD | 2.5 % | 97.5 % | |
|---|---|---|---|---|
| \(\alpha\) | 0.5432018 | 0.0825785 | 0.3855775 | 0.705205 |
| \(\sigma^2\) | 37.5198433 | 5.4763238 | 28.2053971 | 49.918038 |
Vertailun vuoksi: \[ \begin{aligned} \textrm{Yule-Walker}:\quad & \hat{\alpha} = 0.547 \quad \hat{\sigma}^2 = 37.66 \\ \textrm{SU-menetelmä}:\quad & \hat{\alpha} = 0.543 \quad \hat{\sigma}^2 = 36.7 \end{aligned} \]
Esimerkki 5.11 (Maanjäristykset (jatk.)) Poistetaan havainto no. 93 (arvo 23). Malli on sama kuin edellä. Lasketaan aikasarjan tasoparametri \(m\) vain havaituista arvoista.
Stanissa puuttuva havainto koodataan parametriksi. Tässä esimerkissä voidaan jakaa data kahteen osioon: havaintoihin \(y_1, \ldots, y_{92}\) ennen puuttuvaa havaintoa ja havaintoihin \(y_{94}, \ldots, y_{99}\) puuttuvan havainnon jälkeen.
scode2 <- "
data {
int<lower=0> n1; // vuosien lukumäärä ennen puuttuvaa havaintoa
int<lower=0> n2; // vuosien lukumäärä puuttuvan havainnon jälkeen
real y1[n1]; // havainnot ennen puuttuvaa havaintoa
real y2[n2]; // havainnot puuttuvan havainnon jälkeen
real m_hat; // prosessin keskiarvo
}
parameters {
real alpha;
real<lower=0> tau;
real y_mis; // puuttuva havainto
}
transformed parameters {
real<lower=0> sigma;
sigma = 1 / sqrt(tau);
}
model {
alpha ~ normal(0.5, 1 / sqrt(5));
tau ~ gamma(0.3, 1);
y1[1] ~ normal(m_hat, 1 / sqrt(0.03));
for (i in 2:n1) {
y1[i] ~ normal(m_hat + alpha * (y1[i - 1] - m_hat), sigma);
}
y_mis ~ normal(m_hat + alpha * (y1[n1] - m_hat), sigma);
y2[1] ~ normal(m_hat + alpha * (y_mis - m_hat), sigma);
for (i in 2:n2) {
y2[i] ~ normal(m_hat + alpha * (y2[i - 1] - m_hat), sigma);
}
}
"
earthq1 <- earthq[1:92]
earthq2 <- earthq[94:99]
m_hat <- mean(c(earthq1, earthq2))
fit2 <- stan(
model_code = scode2,
data = list(
n1 = length(earthq1), n2= length(earthq2), m_hat = m_hat,
y1 = earthq1, y2 = earthq2
),
iter = 2000,
verbose = FALSE
)Tulokseksi saadaan
| Mean | SD | 2.5 % | 97.5 % | |
|---|---|---|---|---|
| \(\alpha\) | 0.558622 | 0.0840797 | 0.3904533 | 0.7246142 |
| \(\sigma^2\) | 37.058701 | 5.5567154 | 27.8950291 | 49.3268809 |
| \(y_{93}\) | 14.273093 | 5.2492908 | 3.9509272 | 24.8738328 |
Saamme nyt marginaaliposteriorin myös puuttuvalle havainnolle \(y_{93}\). Tämän jakauman odotusarvo on 14.273093 ja keskihajonta 5.2492908 ja 95 %:n posterioriväli (3.9509272, 24.8738328).