2 Hierarkkiset mallit
2.1 Aineiston rakenne
Havaintoaineistoissa on usein rakenne (hierarkia), joka vaikuttaa havaintoyksiköiden välisiin riippuvuussuhteisiin. Tällaista aineistoa kutsutaan myös klusteroituneeksi. Yksinkertainen esimerkki on koululaisia koskeva data, jossa hierarkiatasot ovat valtio, kunta, koulu, luokka ja oppilas. Tällaisen datan mallintamiseen käytetään yleisesti hierarkkisia malleja. Bayesiläisessä hierarkkisessa mallissa osa parametreista riippuu toisista parametreista, joita kutsutaan hyperparametreiksi.
2.2 Graafiset mallit
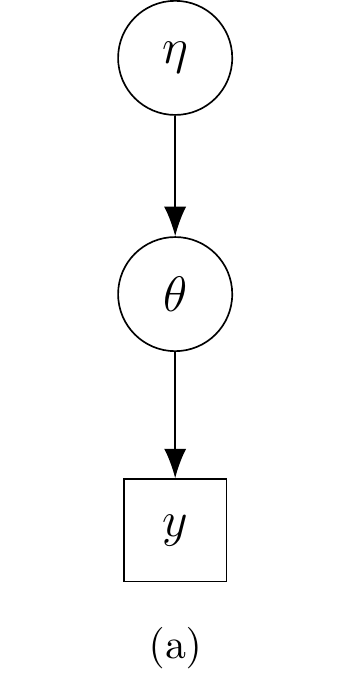
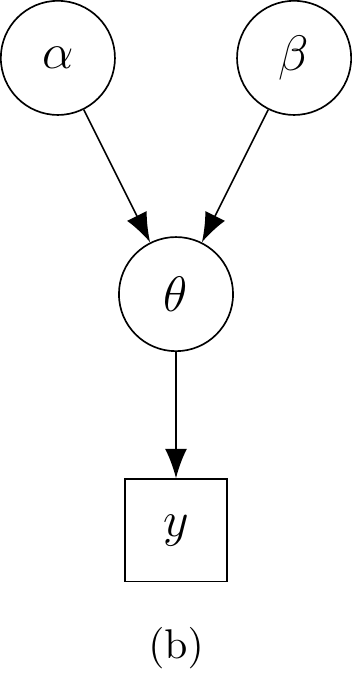
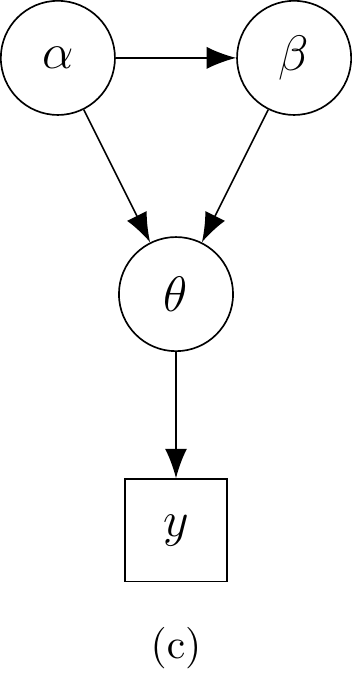
Hierarkkinen malli esitetään usein suunnatun silmukattoman graafin avulla (Directed Acyclic Graph, DAG). Yleisen käytännön mukaisesti havaittuja muuttujia ja tunnettuja vakioita merkitään graafissa neliöillä ja tuntemattomia parametreja ja latentteja muuttujia ympyröillä. Nuolet osoittavat muuttujien ja parametrien väliset riippuvuussuhteet. Kuvassa 2.1 on esitetty kolme esimerkkiä graafisesta mallista.
2.3 Vaihdannaisuus
Havainnot (satunnaismuuttujat) ovat (äärellisesti) vaihdannaisia (finitely exchangeable), jos niiden järjestyksen (indeksien) vaihtaminen ei muuta yhteisjakaumaa. Tällöin havainnoille \(y_1,\ldots,y_n\) ja mille tahansa permutaatiolle \(\pi(1),\ldots,\pi(n)\) pätee \[ p(y_1,\ldots,y_n) = p(y_{\pi(1)},\ldots,y_{\pi(n)}). \] Riippumattomuudesta seuraa vaihdannaisuus, mutta vaihdannaiset satunnaismuuttujat voivat olla riippuvia. Jos havainnot eivät ole vaihdannaisia, ne voivat olla ehdollisesti vaihdannaisia. Käytännössä ehdollinen vaihdannaisuus saavutetaan yleensä olettamalla, että havainnot ovat riippumattomia ehdolla parametrit. Syvällinen ja teoreettisesti merkittävä de Finettin esityslause lähtee kuitenkin liikkeelle (äärettömästä) vaihdannaisuudesta ja johtaa sen perusteella Bayes-tilastotieteen koneiston. Ääretön jono satunnaismuuttujia on (äärettömästi) vaihdannainen, jos mikä tahansa äärellinen osajono on vaihdannainen. Laajennetun version de Finettin lauseesta voi yksinkertaistettuna esittää seuraavasti
Lause 2.1 Tiettyjen säännöllisyysehtojen vallitessa äärettömästi vaihdannaisen jonon osajonon \(y_1,\ldots,y_n\) yhteisjakauman voi esittää muodossa \[ p(y_1,\ldots,y_n) = \int \prod_{i=1}^n p(y_i|\theta)p(\theta)\, d\theta \] jollekin jakaumalle \(p(\theta)\).
Lauseen perusteella vaihdannaiset muuttujat voidaan tulkita ehdollisesti riippumattomaksi ja samoin jakautuneiksi satunnaismuuttujiksi jostakin parametrisesta jakaumasta \(p(\cdot|\theta)\), jonka parametrille \(\theta\) käytetään priorijakaumaa \(p(\theta)\).
2.4 Hierarkkisen mallin sovittaminen
Tarkastellaan hierarkkisen mallin sovittamista käytännön esimerkin avulla.
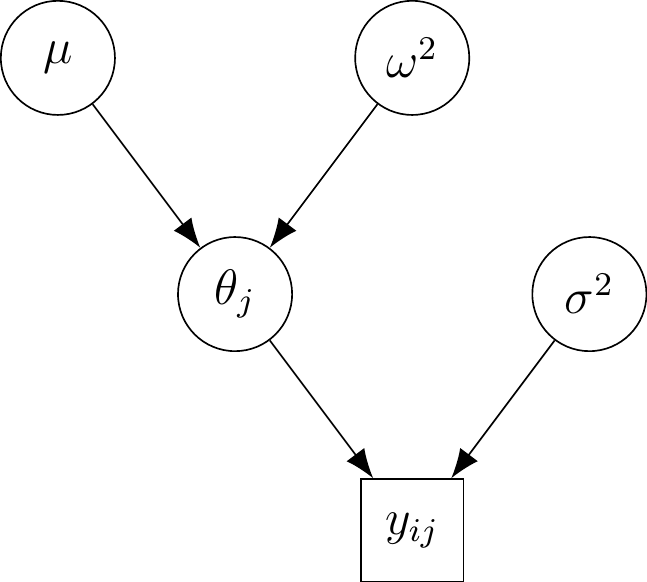
Esimerkki 2.1 (PISA-tutkimus) PISA-tutkimuksessa on mitattu oppilaiden lukutaitoa. Aineisto sisältää tiedon koulusta (koodattuna), mutta ei sisällä tietoa luokasta tai kunnasta. Olkoon \(y_{ij}\) koulun \(j\) oppilaan \(i\) saama pistemäärä. Pistemäärät on standardoitu siten, että kansainvälisen vertailujakauman keskiarvo on 500 ja hajonta 100. Aineistossa on 4403 oppilasta 148 eri koulusta. Ajatellaan, että oppilaiden osaamisessa voi olla koulukohtaisia eroja eli saman koulun oppilaat on osaamistasoltaan enemmän samankaltaisia kuin eri koulujen oppilaat. Kuvataan koulun \(j\) keskimääräistä tasoa parametrilla \(\theta_j\). Koska normaalijakaumaoletus vaikuttaa tässä tapauksessa perustellulta, valitsemme malliksi \[ y_{ij} \sim \operatorname{N}(\theta_j,\sigma^2), \] missä \(\sigma^2\) on varianssiparametri (yhteinen kaikille kouluille). Parametreille \(\theta_j\) ja \(\sigma^2\) tarvitsemme priorijakaumat.
Koska tutkimuksessa mukana olevat koulut ovat satunnaisotos Suomen kaikista kouluista, on luontevaa olettaa koulukohtaisille osaamistasoille oma jakauma. Mallinnamme tätä populaatiojakaumaa normaalijakaumalla \[ \theta_j \sim \operatorname{N}(\mu,\omega^2), \] missä \(\mu\) ja \(\omega^2\) ovat koulutason odotusarvo- ja varianssiparametri (hyperparametreja). Odotusarvolle valitsemme priorin \[ \mu \sim \operatorname{Tas}(0,1000). \] Varianssiparametreille oletamme heikosti informatiiviset priorit \[ \begin{aligned} \sigma^{-2} &\sim \textrm{Gamma}(0.01,0.01) \\ \omega^{-2} &\sim \textrm{Gamma}(0.01,0.01). \end{aligned} \] Malliin liittyvä DAG on esitetty kuvassa 2.2.
Esimerkki 2.2 (Haastattelun stressivaikutus) Kokeessa osallistujilta (kiinteä lukumäärä) mitataan kyselyllä, onko henkilö kokenut ainakin yhden stressitapahtuman kuukausittain haastattelutapahtumaa edeltävänä 18 kuukauden aikana.
Tutkitaan, onko haastattelutapahtuman läheisyydellä vaikutusta stressitilaan sovittamalla yksinkertainen Poisson-jakauma.
On siis havaittu stressitapahtumien lukumäärä kuukausittain \(y_1, \ldots, y_{18}\). Malli tapahtumille on \[ y_i|\lambda_i \sim \textrm{Poisson}(\lambda_i), \quad \log\lambda_i = \beta_0 + \beta_1 i, \] missä havainnot \(y_i|\lambda_i\) oletetaan ehdollisesti riippumattomiksi. Prioriksi valitaan tasajakauma: \[ p(\beta_0, \beta_1) \propto 1. \] Tällöin posterioriksi saadaan \[ p(\beta_0, \beta_1|y) \propto \exp \left(\sum_{i=1}^{18} \left[y_i(\beta_0 + \beta_1 i) - \exp(\beta_0 + \beta_1 i)\right] \right). \] Malliin liittyvä DAG on esitetty kuvassa 2.3

Tässä ongelmassa kiinnostuksen kohteena on erityisesti parametri \(\beta_1\) eli haastattelun läheisyyden vaikutus stressiin.
Huom. Yksilötason vaihtelua ei saada mallinnetuksi, koska kustakin henkilöstä on vain yksi havainto. Vaihtelun mallintamiseksi tarvittaisiin toistomittauksia.