| Päätös | Poutaa | Sadetta |
|---|---|---|
| Kotiin jääminen | 3 | 3 |
| Ulos ilman sateenvarjoa | 6 | 1 |
| Ulos sateenvarjon kanssa | 2 | 4 |
6 Päätöksentekoteoriaa
6.1 Päätöksenteko Bayes-ongelmana
Päätöksenteossa tavoitteena on valita paras päätös \(d\) mahdollisten päätösten joukosta \(\mathcal{D}\). Päätöksen seurauksia kuvaa hyötyfunktio \(U(d,\theta)\), joka kertoo päätöksestä \(d\) seuraavan utiliteetin eli hyödyn, kun maailman tila on \(\theta\). Maailman tilaan liittyy yleensä epävarmuutta, jota bayesilaisittain kuvataan posteriorijakaumalla \(p(\theta | y)\). Optimaalinen päätös maksimoi odotetun hyödyn \[ U(d | y)= \int U(d,\theta) p(\theta | y)\, d\theta. \] Hyötyä mitataan tavallisimmin rahassa, mutta hyöty ei välttämättä ole lineaarinen funktio rahan suhteen.
Usein päätöksentekotilanne on kaksi- tai useampivaiheinen siten, että ensimmäinen päätös koskee lisätietojen hankkimista. Merkitään tutkimusasetelmaa (design) symbolilla \(\eta\). Yksinkertaisimmillaan \(\eta\) pelkistyy otoskooksi, joka tutkijan tulee valita. Asetelmaan \(\eta\) liittyvä maksimoitu odotettu hyöty saadaan kaavalla \[ \overline{U}(\eta) = \int_{\mathcal{Y}} \left[\max_{d \in \mathcal{D}} \int_{\Theta} U(d,\theta) p(\theta | y)\, d\theta\right] p(y | \eta)\, dy. \] Asetelma \(\eta_0\) tarkoittaa, että uutta tietoa ei kerätä lainkaan. Päätöksenteko perustuu tällöin ainoastaan prioritietoon.
6.2 Informaation arvo
Lisätietojen avulla käsitys maailman tilasta tarkentuu ja päätöksen odotettu hyöty kasvaa. Oletetaan, että hyötyä mitataan suoraan rahassa. Tällöin odotetun hyödyn muutosta kutsutaan informaation (rahalliseksi) arvoksi ja se saadaan erotuksena \[ \overline{U}(\eta) - \overline{U}(\eta_0) = \int_{\mathcal{Y}} \left[ \max_{d \in \mathcal{D}} \int_{\Theta} U(d,\theta) p(\theta | y )\, d\theta \right]p(y | \eta)\, dy -\max_{d \in \mathcal{D}} \int_{\Theta} U(d,\theta) p(\theta)\, d\theta. \tag{6.1}\] Lisätietojen hankkimiseen liittyviä kustannuksia tulee verrata informaation arvoon. Informaation arvo 6.1 on mahdollista yleistää tilanteeseen, jossa hyötyä ei mitata suoraan rahassa.
6.3 Esimerkkejä
Päätöksentekoa ja informaation arvon käsitettä selvennetään kahdella esimerkillä.
Esimerkki 6.1 (Sateenvarjo-ongelma) Herra Bayes harkitsee kolmea vaihtoehtoa, jotka ovat A) kotiin jääminen, B) lähteminen ulos ilman sateenvarjoa ja C) lähteminen ulos sateenvarjon kanssa. Edellisen päivän sääennusteen mukaan sateen todennäköisyys on 0.5. Päätöksiin ja säätilaan liittyvät hyötyfunktion arvot on esitetty taulukossa 6.1. Oletetaan, että viimeisin sääennuste antaa täsmällisen tiedon päivän säästä (sataa tai ei sada todennäköisyydellä 1). Kuinka paljon herra Bayesin kannattaa enintään maksaa tästä tiedosta?
Lasketaan ensin optimaalinen päätös, kun käytettävissä on tieto edellisen päivän sääennusteesta. Odotetuiksi hyödyiksi saadaan päätökselle A: \(0.5 \cdot 3 + 0.5 \cdot 3 = 3\), päätökselle B: \(0.5 \cdot 6 + 0.5 \cdot 1 = 3.5\) ja päätökselle C: \(0.5 \cdot 2 + 0.5 \cdot 4 = 3\). Päätös B, ulos lähteminen ilman sateenvarjoa, on siis optimaalinen päätös, koska odotettu hyöty on suurin.
Tarkastellaan seuraavaksi päätöksentekotilannetta, jossa päivän säätila tunnetaan. Taulukosta 6.1 nähdään, että poutasäällä optimaalinen päätös on lähteä ulos ilman sateenvarjoa ja sadesäällä optimaalinen päätös on lähteä ulos sateenvarjon kanssa. Odotettu hyöty on siis \(0.5 \cdot 6 + 0.5 \cdot 4 = 5\). Huomaa, että laskussa tarvitaan sateen prioritodennäköisyyttä, vaikka päätös vaihtoehtojen A, B ja C välillä tehdäänkin ilman epävarmuutta säätilasta.
Täsmällisestä sääennusteesta kannattaa siis maksaa enintään \(5-3.5=1.5\). Tämä erotus on informaation arvo.
Esimerkki 6.2 (Kalankasvattajan ongelma) Kalankasvatusaltaassa on 10 000 kalaa. Tuntematon osuus kaloista kantaa tautia, joka ei tartu toisiin kaloihin mutta johtaa hoitamattomana kuolemaan. Sairaat kalat on mahdollista parantaa lääkitsemällä koko allas, mikä maksaa 15 000 euroa. Kasvatusjakson lopussa kasvattaja myy elossa olevat kalat 5 euron kappalehintaan. Käytettävissä oleva ennakkotieto sairaiden kalojen osuudesta \(\theta\) voidaan esittää priorijakaumana \(p(\theta)=\textrm{Beta}(\theta|3,3)\).
Sairaiden kalojen osuudesta on mahdollista kerätä lisätietoja diagnosoimalla satunnaisesti valittuja kaloja. Diagnostinen testi maksaa 10 euroa kalaa kohden. Kuinka monta kalaa kasvattajan kannattaa diagnosoida ennen hoitopäätöksen tekemistä?
Aluksi määrittelemme kalojen rahallisen arvon \[ v(\theta,d) = \begin{cases} (1-\theta) 10000 \times 5 ,& d = \text{ei lääkitystä} \\ 10000 \times 5 - 15000 , & d = \text{lääkitys}, \end{cases} \] jossa luvut ovat euroja. Oletamme hyödyn olevan suoraan verrannollinen rahalliseen arvoon, jolloin \[ U(\theta,d,n_\eta,y) = U(\theta,d,n_\eta) =v(\theta,d) - 10n_\eta. \tag{6.2}\] Koska ennakkotietojen perusteella \(\operatorname{E}(\theta)=3/(3+3) = 0.5\), optimaalinen päätös pelkän prioritiedon perusteella on kasvatusaltaan hoitaminen, joka johtaa maksimoituun odotettuun hyötyyn \(\overline{U}(\eta_0)=35 000\). Jotta lisätiedon hankkiminen kaloja diagnosoimalla olisi järkevää, maksimoidun odotetun hyödyn tulisi ylittää 35 000 euroa.
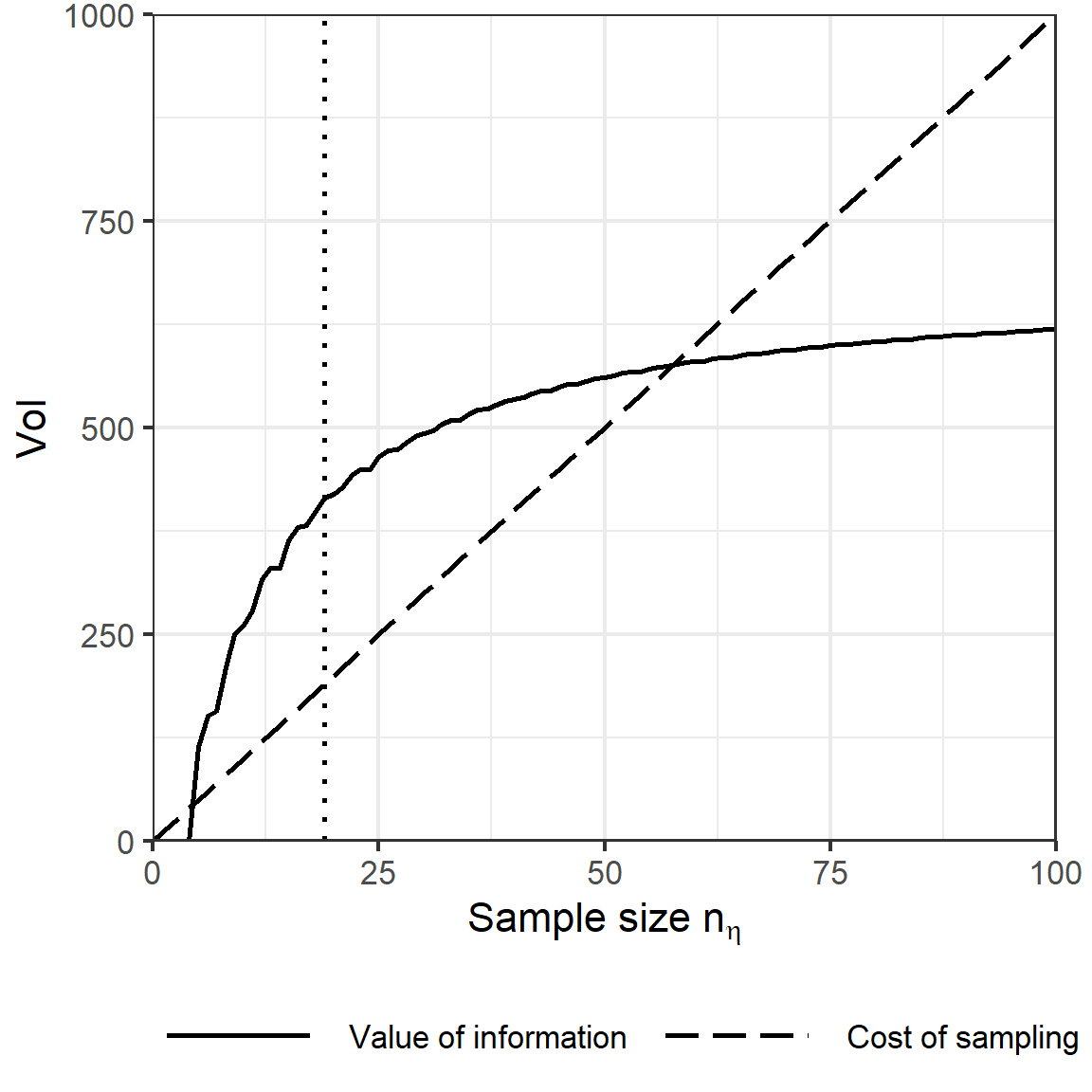
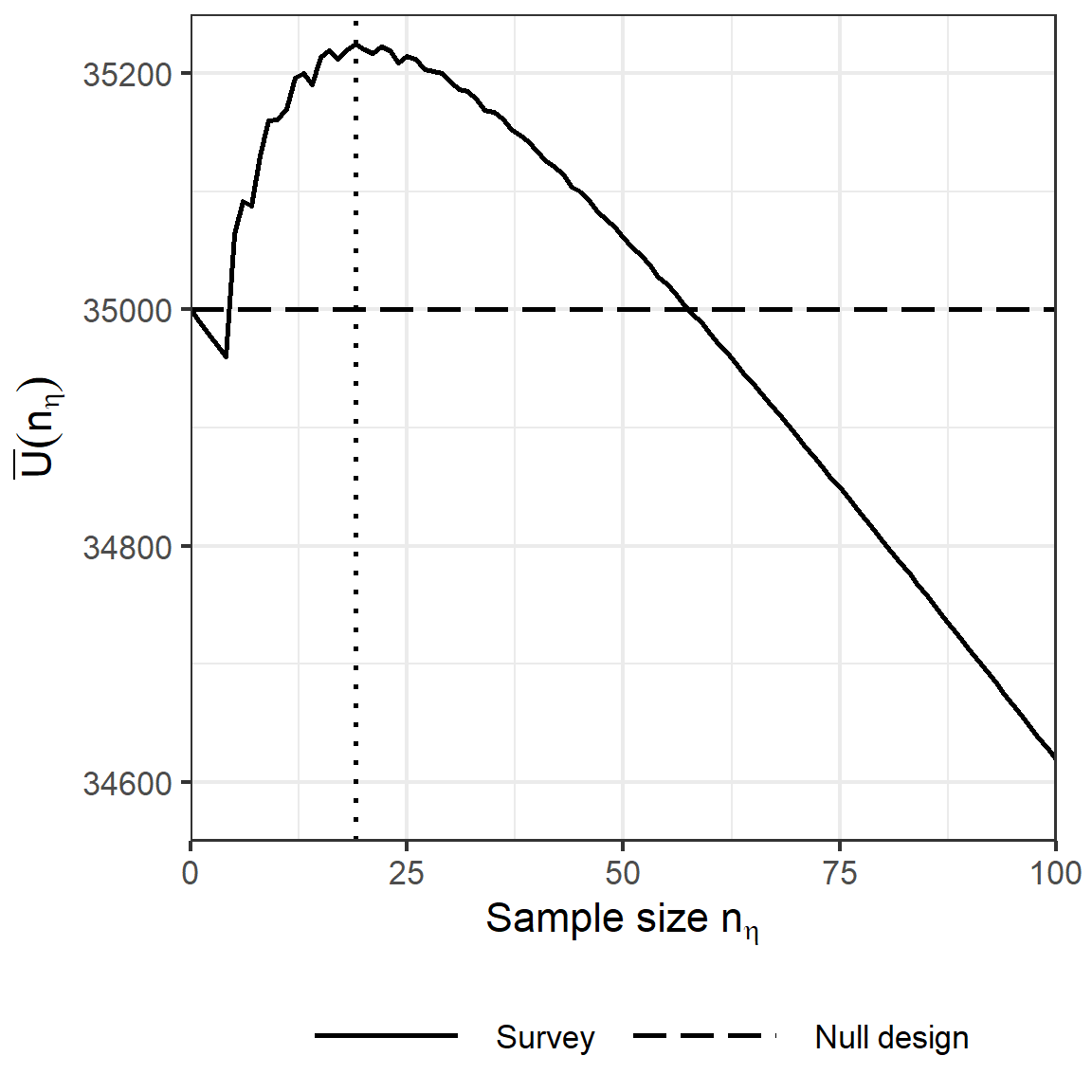
Oletetaan yksinkertaisuuden vuoksi, että otanta toteutetaan palauttaen. Olkoon \(n_{\eta}\) diagnosoitujen kalojen määrä ja \(y\) tautia kantavien kalojen määrä otoksessa. Päädytään malliin \(y|\theta,n_{\eta} \sim \textrm{Bin}(y|n_{\eta},\theta)\). Otoskokoon \(n_{\eta}\) liittyvä odotettu hyöty saadaan laskemalle jokaiselle mahdolliselle sairaiden kalojen määrälle \(y\) maksimoitu odotettu hyöty ja painottamalla näitä kunkin mahdollisuuden prioritodennäköisyydellä.Kaavana tämä voidaan esittää muodossa \[ \overline{U}(n_\eta)= \sum_{y=0}^{n_\eta}\mbox{Beta-Bin}(y | n_\eta, 3,3) \max_{d \in\mathcal{ D}} \int U(\theta,d,n_\eta)\mbox{Beta}(\theta | y+3, n_\eta-y+3)d\theta. \] missä \(U(\theta,d,n_\eta)\) on määritelty kaavassa @ref(eq:farmersutility). Maksimoitua odotettua hyötyä \(\overline{U}(n_\eta)\) laskettaessa hyötyfunktio \(U(\theta,d,n_\eta)\) integroidaan mahdollisten otosten ja posteriorijakauman \(p(\theta | y)\) ylitse sekä maksimoidaan päätöksen \(d\) suhteen. Vaihtoehtoinen tapa ratkaista ongelma on laskea otokseen \(n_\eta\) liittyvä informaation arvo \[ \overline{v}(n_\eta)-\overline{v}(n_0) = \sum_{y=0}^{n_\eta}\mbox{Beta-Bin}(y | n_\eta, 3,3) \max_{d \in\mathcal{ D}} \int v(\theta,d)\mbox{Beta}(\theta | y+3, n_\eta-y+3)d\theta-35000, \] ja verrata sitä otantakustannuksiin. Molemmat tavat johtavat samaan lopputulokseen. Kuvassa 6.1 esitetään informaation arvo, otantakustannukset ja maksimoitu odotettu hyöty, kun otoskoko vaihtelee nollasta sataan. Hyöty on positiivinen, kun otoskoko on välillä \([5,57]\). Suurin hyöty saavutetaan, kun \(n_\eta=19\).