GRAPH THEORY
NETWORK MODELS
Käsitteitä Englanninkielisestä sanastosta Sosiometrisistä verkoista Karttojen neliväritysongelmasta
Verkko eli graafi koostuu solmuista (node, vertex), väleistä (edge, arc, line) sekä välien ja solmujen erottamista alueista (face). Eulerin kaava määrittää näiden välille suhteen: jos v, e ja f ovat solmujen, välien ja alueiden määrät, niin v - e + f =2. Alueet liittyvät enemmänkin ns. topologiseen verkkoteoriaan eikä niistä tarvitse operaatiotutkimuksen yhteydessä juuri välittää. Alla verkko ja sitä kuvaava matriisi.

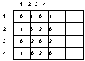
Königsbergin sillat verkkona ja matriisina
Verkkoteorian syntyhetkenä voidaan pitää vuotta 1736, jolloin Leonhard Euler julkaisi artikkelinsa Königsbergin siltojen ongelmasta. Königsbergin eli nykyisen Kaliningradin läpi virtasi Pregel-joki, jonka keskellä oli saari. Tehtävänä oli kulkea jokaisen 7:n sillan yli kerran siten että yhtäkään siltaa ei ylitetty kahdesti. Euler ratkaisi ongelman (ei ole mahdollista) ja ratkaisua tehdessään tuli piirtäneeksi kuvan (yllä oleva verkko), jota pidetään "kaikkien verkkojen äitinä" Sanaa "graph" käytettiin ensimmäisen kerran vuonna 1878 (Sylvester). Sana on peräisin kemiasta ("graphic notation"), joka koki murroksen 1850-luvulla kun alettiin ymmärtää aineiden kemiallista rakennetta ja tarvittiin selkeä tapa kuvata sitä. Hieman aikaisemmin oli Kirchoff kehittänyt sähkön virtausta koskevat lakinsa, joiden kuvaamisessa tarvittiin verkkoja apuna (electrical networks). Toisen maailmansodan jälkeen alkoi verkkoteoria operaatiotutkimuksen tavoin kehittyä nopeasti ja syynä oli tietenkin tietokoneiden tulo. Sodan aikana myös Königsbergin siltojen ongelma ratkaistiin hieman Gordionin solmun tavoin: sillat tuhottiin ja jälleenrakennuksessa niiden lukumäärä muuttui niin että ongelma oli mahdollista ratkaista!
On syytä muistaa, että verkkoteoria on työväline, tapa hahmottaa ongelmia, muiden joukossa. Siksi sen sovellusalue onkin rajaton ja usein ongelman esittäminen verkkoteorian muodossa onkin eniten kiinni kyvystä hahmottaa sen keskeiset rakenteet sekä mielikuvituksesta. On olemassa tietoverkkoja, liikenneverkkoja, kemiallisia verkkoja, sosiometrisiä verkkoja, lingvistisiä verkkoja, jne. Verkkoteorian merkitys lineaarisessa optimoinnissa käy ilmi alla olevasta kuvasta.
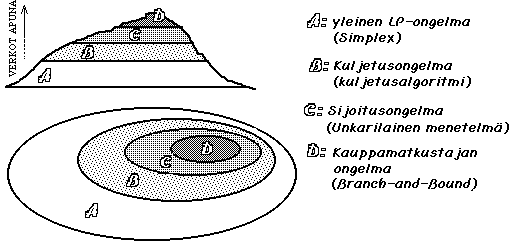
Kuvasta nähdään kuinka
kuljetusongelma on tavallisen LP-ongelman erikoistapaus, sijoitusongelma kuljetusongelman jne. Kunkin ongelman yhteyteen on sulkuihin merkitty tavallisin ratkaisumenetelmä ja kuten itse ongelman kohdalla myös ratkaisumenetelmät ovat Simplex-menetelmän hienostuneempia sovelluksia. Kun alempana olevaa tasokarttaa tarkastellaan sivuprofiilista niin siinä verkkoteorian merkitys kasvaa ylöspäin mentäessä, mutta myös aivan tavallista LP-ongelmaa voidaan projisoida verkkoteoriaan kun muistetaan että matriisi voidaan aina kuvata myös verkkona. Yllä on Königsbergin siltaverkko esitetty matriisina, myös muita esitystapoja on olemassa. Muualla operaatiotutkimuksen alueella eritoten projektinhallinnan yhteydessä joudutaan turvautumaan verkkoteorian menetelmiin.Eräitä keskeisiä
käsitteitäVerkkoteorian (graafiteorian) käsitenimistö on varsin kirjava ja oman vaikeutensa on aiheuttanut se että samasta asiasta on monesti käytetty lähteestä riippuen eri nimeä, ja päinvastoin, sama nimi saattaa joskus tarkoittaa eri asiaa. Oheen on kerätty eräitä keskeisiä verkko- eli graafiteorian käsitteitä. Lista voisi olla huomattavasti pidempi sillä suuri joukko käsitteitä, jotka eivät suoraan liity operaatiotutkimuksen ja matematiikan peruskurssiin, on karsittu pois. Käsitteet on esitetty siten, että ensin on listattu keskeisimmät tiivistetyssä muodossa, josta ne voi nopeasti silmäillä läpi, ja
verkkoteorian käsitteitä sivuilta löytyy sitten yksityiskohtaisempi kuvaus selventävien kuvien kanssa.Suunnattu verkko (directed graph, digraph)
on sellainen verkko, jonka jokaiselle välille on annettu jokin suunta.Painotettu verkko (weighted graph) on suunnattu verkko, jonka väleille ja/tai solmuille on annettu painoarvot, esimerkiksi pituus, aika, tavaramäärä jne. Erityisesti välien suhteen painotetusta verkosta nimitystä network.
Kuljetusverkko (transport network) puolestaan on määritelty äärelliseksi ja yhtenäiseksi välien suhteen painotetuksi verkoksi, joka ei sisällä luuppeja.
Tasoverkko (planar graph) on verkko, joka voidaan piirtää s.e. mikään väli ei leikkaa toistaan. Tasoverkolle muodostetaan duaali sijoittamalla yksi solmu jokaiseen alueeseen ja yhdistämällä saadut solmut toisiinsa siten, että jokainen näin syntyvä väli leikkaa jokaisen alkuperäisen verkon välin täsmälleen yhden kerran.
Täydellinen verkko (complete graph) on verkko, jonka jokaisesta solmusta on väli verkon jokaiseen muuhun solmuun välien määrä on e= v(v-1)/2 kun v on solmujen määrä.
Klikki on verkon sisältämä täydellinen aliverkko. Esimerkiksi sosiometrisen verkon klikit kuvaavat tiiviitä sosiaalisia yhteisöjä.
Kaksijakoisen verkon (bipartite graph) solmut voidaan jakaa kahteen joukkoon siten, että kaikki verkon välit ovat ainoastaan näiden joukkojen yhdysvälejä. Kuljetus- ja sijoitusongelmissa käsitellään kaksijakoisia verkkoja. Vastaavasti on määritelty k-jakoinen verkko, josta esimerkkinä voi olla kauttakuljetusongelma (transshipment problem).
Silmukka eli sykli on sellainen polku, jonka alku- ja loppusolmu ovat samat. Hamiltonin silmukka on suljettu polku, joka kulkee verkon kaikkien solmujen kautta siten, että kussakin solmussa käydään vain kerran. Kauppamatkustajan ongelma on tyypillinen esimerkki tehtävästä, jossa haetaan Hamiltonin silmukkaa.
Eulerin ketju on puolestaan silmukka, joka kulkee verkon jokaisen välin kautta täsmälleen kerran. Verkkoteorian johdantosivulla mainittu Königsbergin siltaverkko ei siis sisällä Eulerin ketjua.
Leikkaussolmu (cutnode) yhtenäisessä verkossa on solmu, jonka poistaminen tekee verkosta epäyhtenäisen. Vastaavasti sellainen väli, jonka poisto hajoittaa verkon on nimeltään silta Esimerkiksi sosiometrisessä verkossa leikkaussolmu voi tarkoittaa sellaista henkilöä, jonka poistuminen hajoittaa yhteisön kahtia.
Kaksi verkkoa ovat isomorfisia jos ja vain jos niiden solmujen ja välien kesken vallitsee yksikäsitteinen vastaavuus siten että jos kaksi solmua on naapurisolmuja yhdessä verkossa niin samat kaksi solmua ovat naapurisolmuja myös toisessa verkossa. Tällaiset verkot voidaan kuvata bijektiivisesti toisilleen.
Jos väli alkaa ja loppuu samaan solmuun niin väliä kutsutaan luupiksi eli lenkiksi.
Jos kahdella eri välillä on samat alku- ja loppusolmut, niin välit ovat rinnakkaisia.
Jos kahdella välillä on ainakin yksi yhteinen solmu niin välit ovat vierekkäisiä.
Yksinkertainen verkko on verkko, jossa ei ole luuppeja eikä rinnakkaisia välejä.
Tasoverkon duaaliverkko saadaan kun sijoitetaan alkuperäisen verkon jokaiseen alueeseen solmu ja korvataan alueita erottavat välit näin syntyviä solmuja yhdistävinä väleinä.
Verkon komplementti eli ulkoverkko saadaan upottamalla verkko täydelliselle verkolle, jolla on sama solmujoukko, ja poistamalla kaikki alkuperäisen verkon välit.
Väliverkko saadaan asettamalla jokaiselle verkon välille uusi solmu ja yhdistämällä vierekkäisille väleille asetetut solmut uusilla väleillä, kukin solmupari yhdellä uudella välillä.
Solmun asteluku on siitä lähtevien välien lukumäärä.
Verkko on yhtenäinen, jos jokainen sen solmuista voidaan yhdistää muihin solmuihin ainakin yhdellä polulla.