Hakemistoon

 

SIMPLEX-MENETELMÄ

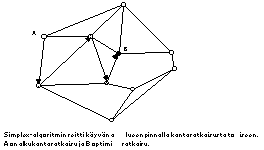
Simplex-menetelmän perusajatuksena on kulkea pitkin käyvän alueen reunaa alkaen yhdestä kulmapisteestä (eli kantaratkaisusta) ja jatkaen sitten johonkin sellaiseen naapurikulmaan, joka on lähempänä optimia. Näin kuljetaan läpi reitti, jonka varrella sivuutetaan osa kantaratkaisuista ennen kuin saavutetaan se kulma, jossa optimaalinen kantaratkaisu sijaitsee.

Menetelmän nimi ei kuvaa sen "yksinkertaisuutta" vaan juontaa juurensa käyvän alueen muodosta. Käypä aluehan on konveksi monikulmio jos muuttujia on kaksi ja monitahokas jos muuttujia on kolme. Mikäli muuttujia on m kpl niin se on m-ulotteinen "hypertahokas", jonka reunalla Simplexissä liikutaan. Tällaista kappaletta kutsutaan matematiikassa simpleksiksi siten, että monikulmio on 2-simpleksi, tavallinen monitahokas 3-simpleksi jne.

 

Itse Simplex-algoritmi on peräisin vuodelta 1947, jolloin George Dantzig sen kehitti.

Menetelmä jakautuu seuraaviin vaiheisiin:

1°

Muunnetaan LP-ongelma kanoniseen muotoon vaihtamalla epäsuuruusmerkit yhtä suuruusmerkeiksi. Tämä tapahtuu siten, että otetaan käyttöön ns. pelivaramuuttujat, jotka eivät muuta kohdefunktion arvoa.

2°

Muodostetaan alkukantaratkaisu. Alkukantaratkaisuun kuuluvat yleensä vain pelivaramuuttujat ja kohdefunktion arvo on 0.

3°

Valitaan kantaan uudeksi muuttujaksi se, jolla on suurin kerroin kohdefunktiossa (kun kyseessä on maksimointi) ja poistetaan kannasta yksi muuttuja. Poistettavan muuttujan valinta selviää oheisesta esimerkistä.

4°

Muutetaan yhtälöryhmää, jota on helpointa käsitellä matriisimuodossa, siten että uuden kantamuuttujan kerroin saa arvon 1 yhdellä rivillä ja muilla riveillä (myös kohdefunktiossa) arvon 0. Käytännössä tämä tapahtuu hakemalla ns. Pivot-alkio, joka sijaitsee samalla sarakkeella kuin uusi kantamuuttuja ja samalla rivillä kuin poistettavan kanta muuttujan kerroin on 1. Pivot-alkiota sopivasti kertomalla ja yhtälöitä summaamalla eli suorittamalla Pivot-operaatio saadaan haluttu muutos aikaan.

Prosessia jatketaan niin kauan kuin kohdefunktiossa on positiivisia kertoimia (kun käytetään esimerkin merkintätapaa).

Esimerkki (sama esimerkki kuin LP-ongelman yhteydessä esitetty, Pivot-alkio on ympyröity):

Max z = 2x1 + x2…………………………….Max z = 2x1 + x2……………………………Alkukantaratkaisu:

x1 + x2 ≤ 4……………Þ…………………..x1 + x2 + x3 = 4……………………………..x3= 4

x1 - 2x2 ≤ 1…………………………………..x1 - 2x2 + x4 = 1……………………………x4= 1 ja x1, x2 = 0

x1, x2 ≥ 0…………………………………….x1, x2, x3, x4 ≥ 0…………………………….z=0

Ensin otetaan kantaan x1 (max{1,2}=2) ja poistetaan x4 (haetaan min{4/1,1/1}=1, sijaitsee rajoiterivillä, jossa x4 on kanta-alkiona). Toisessa vaiheessa otetaan kantaan x2 ja poistetaan x3 (min{1/-2,3/3} >= 0 (siis 1), rajoiterivillä, jolla x3 on kanta-alkiona). Pivot alkiot eri vaiheissa on ympyröity kuvassa.

 

Prosessi päättyy tällä kertaa kahden vaiheen jälkeen kun kohdefunktion kaikki kertoimet ≤0. Optimiarvoksi saadaan näin 7 kun x1=3 ja x2=1. Tämä merkintätapa on vain yksi monista.

Perus-Simplexistä löytyy lukuisia eri tavoin tehostettuja muunnelmia (mm. "korjaava" Simplex eli Revised Simplex). Myös muita, tavanomaista Simplexiä tehokkaampia menetelmiä on kehitetty seulomaan optimi kantaratkaisujen joukosta.

 

Demot 7: 1. ja 4.

 

 

Operaatiotutkimuksen ja matematiikan perusteet, Tietojenkδsittelytieteiden laitos, Informaatioteknologian tiedekunta, Jyvδskylδn yliopisto