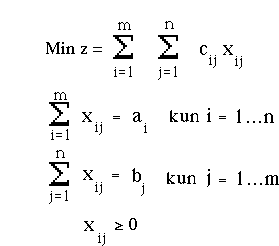
KULJETUSONGELMA
Kuljetusongelmassa on joukko tavaran tuottajia (m kpl) ja joukko tavaran hankkijoita (n kpl). Kukin tuottaja voi toimittaa vain tietyn määrän tavaraa (ai, i=1..m) ja kukin hankkija tarvitsee tietyn määrän tavaraa (bj, j=1..n). Kuljetuskustannuksia tuottaja/hankkija-parin välillä merkitään cij. Tarkoituksena on suunnitella toimitetun tavaramäärän (xij) kuljetuksen jakautuminen tuottajilta hankkijoille siten että kustannukset tulevat minimoitua kun samalla huomioidaan annetut rajoitukset. Kuljetusongelmaa voidaan kuvata kaksijakoisella suunnatulla verkolla (koostuu kahdesta solmujoukosta vailla sisäisiä välejä, kaksijakoinen=bipartite
, suunnattu verkko=digraph). Kuljetusongelma voidaan esittää LP-ongelmana allaolevassa muodossa:
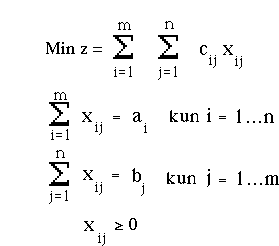
Kuljetusongelma voidaan ratkaista mm. siten että muodostetaan kustannusmatriisi, josta haetaan jokin alkukantaratkaisu, jossa on aina m+n-1 alkiota. Alkukantaratkaisun pohjalta lähdetään hakemaan optimiratkaisua kuljetusalgoritmin avulla. Samalla tehtävällä voi olla useitakin optimiratkaisuja. Kantaratkaisun hakemiseen voidaan käyttää mm. seuraavia menetelmiä: luoteiskulmamenetelmä, minimikustannusmenetelmä tai Vogelin menetelmä. Näistä ensin mainittu on vaivattomin, mutta antaa yleensä kehnoimmat alkuarvot. Paras tulos saadaan Vogelin menetelmällä, joka on työläin mutta palkitsee vähäisemmillä iteraatioilla itse kuljetusalgoritmissa.
Esimerkki:
A tuottaa tavaraa 5 yksikköä ja B 10 yksikköä. Hankkijat 1, 2 ja 3 tarvitsevat k.o. tavaraa 3, 8 ja 4 yksikköä. Kuljetuskustannukset ovat markkoina: A1=9, A2=3, A3=1, B1=7, B2=5, B3=5. Haetaan ohessa alkukantaratkaisut luoteiskulmamenetelmää ja Vogelin menetelmää käyttäen:
1° Luoteiskulmamenetelmä (lähdetään "luoteiskulmasta" ja sijoitetaan ruutuun suurin mahdollinen tavaramäärä, poistetaan yksi rivi tai sarake):

2° Vogelin menetelmä (lasketaan kullekin riville ja sarakkeelle sakkoluku - kahden pienimmän arvon erotus - ja valitaan suurimman sakkoluvun riviltä/sarakkeelta pienimmän kustannuksen ruutu, sijoitetaan ruutuun suurin mahdollinen tavaramäärä):
Lopputulokset:
Luoteiskulmamenetelmällä 3*9+2*3+6*5+4*5 = 83 mk
Vogelin menetelmällä 3*7+7*5+1*3+4*1 = 63 mk
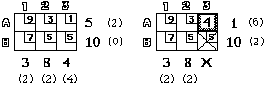
Luoteiskulmamenetelmällä saatiin kantaratkaisu, jonka ulkopuolelle jäivät ruudut A3 ja B1. Kuljetusalgoritmissa lasketaan sakot näille kantaratkaisun ulkopuolelle jääneille ruuduille, joita esimerkkitapauksessa on vain kaksi. Sakon arvo saadaan kiertämällä ruutua vastaava polku (ks. sivun alin kuva) kannassa ja vuorotellen summaamalla ja vähentämällä kustannukset. Polku kierretään liikkumalla vuoroin pysty- ja vaakasuoraan, kiertosuunta ei vaikuta tulokseen. Saadaan:
S(A3) = A3 - B3 + B2 - A2 = 1 - 5 + 5 - 3 = -2 ja S(B1) = B1 - B2 + A2 - A1 = 7 - 5 + 3 - 9 = -4. Algoritmi pysähtyy jos yksikään lasketuista sakoista ei ole negatiivinen. Mikäli negatiivisia sakkolukuja löytyy niin valitaan kantaan itseisarvoltaan suurimman arvon omaava ruutu; tässä tapauksessa siis B1. Kuormitus uudelle kantaruudulle saadaan kiertämällä sama polku jolta sakko laskettiin ja siirtämällä polulta kyseiseen kantaruutuun suurin mahdollinen kuorma. Esimerkkitapauksessa se on min{3,6} = 3. Kun polku kierretään ympäri niin siirretään kuormia ruudusta toiseen siten että lopputilanteessa on tasapaino jälleen saavutettu eli rivi ja sarakesummat täsmäävät.Siis seuraavasti (kuvataan tässä esityksessä nuolella
¿ kuorman siirtymistä ruutuun):B1
¿ +3 Þ 3, A1 ¿ -3 Þ 0, A2 ¿ +3 Þ 5, B2 ¿ -3 Þ 3. Se ruutu, jonka kuormitus nollautuu (A1) poistuu kannasta. Jos useamman ruudun kuorma tulee nollaksi niin kannasta poistetaan ruutu, jolla on korkeimmat kustannukset.
Lasketaan uuden kantaratkaisun ulkopuolelle jääneiden ruutujen sakot:
S(A1) = 9 - 3 + 5 - 7 = 4 ja S(A3) = 1 - 5 + 5 - 3 = -2. Kantaan otetaan siis ruutu A3, johon siirretään kuormaa 4 yksikköä. Siis: A3 ¿ +4 Þ 4, B3 ¿ -4 Þ 0, B2 ¿ +4 Þ 7, A2 ¿ -4 Þ 1, joten kannasta poistuu B3. Ulkopuolelle jääneet ruudut ovat nyt A1 ja B3, joiden sakot, S(A1) = 9 - 7 + 5 - 3 = 4 ja S(B3) = 5 - 5 + 3 - 1 = 2 ovat molemmat positiivisia. Näiden algoritmi päättyy ja saatu ratkaisu on optimi. Huomataan, että se on sama kuin Vogelin menetelmällä haettu alkukantaratkaisu. Ratkaisua voidaan kuvata alla olevalla kaksijakoisella suunnatulla verkolla.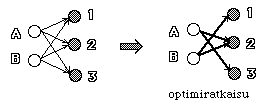
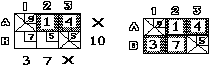
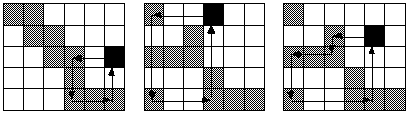
Kolme esimerkkiä polun määräytymisestä. Harmaat ruudut (6+5-1= 10 kpl) kuuluvat kantaan. Mustaa ruutua tutkitaan.
Demot 8: 3.-5. ja 9: 1.