LP = linear programming = lineaarinen ohjelmointi = lineaarinen optimointi. LP-malliin kuuluu maksimoitava tai minimoitava kohdefunktio eli objektifunktio, sekä kohdefunktion muuttujia koskevat rajoite-epäyhtälöt. Sekä kohdefunktio että rajoitteet ovat lineaarisia, mikä tarkoittaa sitä että esimerkiksi tavallisessa xy-koordinaatistossa ne ovat suoria, kolmiulotteisessa xyz-koordinaatistossa tasopintoja jne...
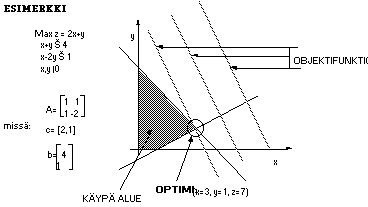
Rajoitteiden erottamaa aluetta kutsutaan nimellä käypä alue. Mikäli käypä alue on olemassa niin se on aina konveksi, mikä tarkoittaa sitä että jos kuviteltu kulkija liikkuu käyvän alueen reunalla niin hän "laskeutuu" jatkuvasti alaspäin. Siis jos käypä alue sijaitsee tasolla ja se kierretään myötäpäivään niin missään vaiheessa ei käännytä vasemmalle (ks. kuva). Konveksi alue voidaan määritellä myös siten että jos kahden sen sisälle asetetun pisteen välille piirretään suora jana niin tämä pysyy koko ajan konveksilla alueella. Käypä alue voi olla myös ääretön tai tyhjä (rajoitteet ovat ristiriitaisia).
LP-ongelmalle haettava optimiratkaisu löytyy käyvän alueen reunalta, paikasta jossa kohdefunktion maksimi (tai minimi) saavutetaan. Jos käypä alue on äärellinen niin optimiratkaisuja on vain yksi tai sitten ääretön määrä (kohdefunktio on saman suuntainen kuin käyvän alueen jokin sivu). Mikäli käypä alue ei olisi konveksi niin optimiratkaisuja voisi olla useampia erillisiä. Jos käypä alue on ääretön niin kohdefunktio voi saada miten suuria (pieniä) arvoja tahansa. Jos käypää aluetta ei ole niin luonnollisesti ei ole optimiratkaisuakaan. Jos lisäksi vaaditaan, että ratkaisun on oltava kokonaisluku niin todellinen optimi voi poiketa huomattavastikin laskemalla saadusta optimista. Tällainen kokonaislukuoptimi voi myös puuttua kokonaan vaikka käypä alue olisikin olemassa.
LP-ongelma standardimuodossa:
Max z = cx, Ax ≤ b, x≥0,
missä A on epäyhtälöryhmän kertoimet sisältävä matriisi ja b rajoitteita esittävä vektori.LP-ongelma kanonisessa muodossa:
Max z = cx, Ax = b, x≥0
Kanonisen muodon ero standardimuotoon on siinä, että rajoite-epäyhtälöt (Ax ≤ b) on keinotekoisesti muutettu rajoiteyhtälöiksi (Ax = b) lisäämällä muuttujien joukkoon ns. pelivaramuuttujat. Ero kanonisen ja standardimuodon välillä on hyvä muistaa erityisesti valmisohjelmistoja käytettäessä. Monet ohjelmistot olettavat kanonisen muodon, joka joskus jopa kulkee standardimuodon nimikkeen alla. Yhtälöissä z on kohdefunktio ja c on kohdefunktion kertoimet sisältävä vektori. A on matriisi, joka sisältää rajoite-epäyhtälöiden kertoimet ja b vektori, joka sisältää epäyhtälöiden rajat. Seuraavaksi yksinkertainen esimerkki:


Jos, kuten tavallista, LP-ongelmassa on muuttujia on enemmän kuin rajoitteita niin rajoite-epäyhtälöt voivat tietenkin pitää paikkansa monillakin eri muuttujien arvoilla. Jos osalle muuttujista annetaan arvoksi nolla siten, että jäljelle jää yhtä monta muuttujaa kuin on rajoitetta niin näille jäljelle jääville löytyy vain yksi ehdot toteuttava ratkaisu. Tällaista ratkaisua kutsutaan kantaratkaisuksi. LP-ongelmalla on useita kantaratkaisuja, jotka sijaitsevat aina käyvän alueen kulmapisteissä. Optimiratkaisu löytyy näiden kantaratkaisujen joukosta. Jos LP-ongelmassa on yhtä monta muuttujaa kuin on rajoiteyhtälöitä niin kantaratkaisuja on vain yksi. Yleensä muuttujia on siis kuitenkin enemmän kuin rajoitteita ja kantaratkaisujen määrä saadaan kaavasta m!/n!(m-n)! (vrt. sama kaava
todennäköisyyslaskennan yhteydessä), missä m on muuttujien ja n rajoitteiden määrä (kaavahan oli esillä jo todennäköisyyslaskennan yhteydessä). Käytännössä kantaratkaisujen määrä voi olla huomattavan suuri sillä jos esimerkiksi m=13 ja n=8 niin soveliaita kantaratkaisuja löytyy 1287 kpl. Olisi kovin epätaloudellista ryhtyä läpikäymään kaikkia kantaratkaisuja optimiratkaisun löytämiseksi niinpä on kehitetty erilaisia menetelmiä optimin hakemiseksi. Tällainen menetelmä on Simplex, josta enemmän seuraavassa luvussa.Kantaratkaisujen määrää voidaan myös supistaa muodostamalla LP-ongelmalle sen duaaliongelma. Vaikka duaaliongelmassa ovatkin eri muuttujat ja rajoitteet niin optimiratkaisu on sama kuin alkuperäisellä eli primaaliongelmalla mikäli molemmilla on ratkaisu. Mikäli toisen ratkaisu on ääretön niin silloin ei toisella ole ratkaisua.
Alkuperäinen primaaliongelma: Max z = cTx, Ax ≤ b, x ≥ 0
Vastaava duaaliongelma: Min z = bTy, ATy ≥ c, y ≥ 0