Single SNS junction¶
We want to calculate for an SNS junction:
The density of states for a given phase difference
The supercurrent-phase relation at a low temperature
See also
Loading libraries¶
First, libraries need to be loaded:
from scipy import *
import usadel1 as u
Specifying the geometry¶
All calculations start with a geometry specification. An SNS junction can be modeled with two S-terminals and one N-wire:
geometry = u.Geometry(nwire=1, nnode=2)
geometry.t_type = [u.NODE_CLEAN_S_TERMINAL, u.NODE_CLEAN_S_TERMINAL]
geometry.w_type = [u.WIRE_TYPE_N]
The wire is connected to both terminals:
geometry.w_ends[0,:] = [0, 1]
Note that all indices are zero-based; the first terminal is 0 and the second 1.
Moreover, currently only clean interface boundary conditions are
implemented. In principle, these would be straightforward to add; the
place to put them would be in sp_equations.f90.
Then, assign a phase difference and energy gap for the terminals:
geometry.t_delta = [100, 100]
geometry.t_phase = [-.25*pi, .25*pi]
and set wire properties
geometry.w_length = 1
geometry.w_conductance = 1
Solving DOS¶
Next, the spectral equations can be solved, and results saved to a file:
solver = u.CurrentSolver(geometry)
solver.set_tolerance(sp_tol=1e-8)
solver.solve_spectral()
solver.save('sns-spectral.h5')
To capture the SNS junction minigap edge correctly at phase
differences 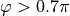 , we need to set a stricter
tolerance
, we need to set a stricter
tolerance 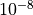 than the default
than the default 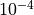 for the
spectral solver. This has an impact on speed, however.
for the
spectral solver. This has an impact on speed, however.
The results can be inspected with any program that can read HDF5
files, for example Matlab (use the supplied scripts/h5load.m
script to load HDF5 files), or Python:
a, b = solver.spectral.a, solver.spectral.b
E, x = solver.spectral.E, solver.spectral.x
dos = real((1 + a*b)/(1 - a*b))
The solver object has attributes
spectral, coefficient, kinetic
that contain the solutions (Riccati parameters)  ,
, 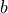 to the spectral equations, the kinetic coefficients,
to the spectral equations, the kinetic coefficients, 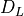 ,
,
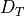 ,
, 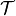 ,
, 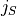 , and the solutions to the
kinetic equations,
, and the solutions to the
kinetic equations, 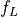 , ,
, , 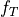 . The Green function
is parameterized in a mixed Riccati–distribution function scheme
. The Green function
is parameterized in a mixed Riccati–distribution function scheme
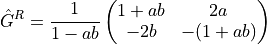
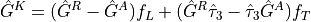
Plot the DOS in the N-wire (lines for different positions are offset from each other):
import matplotlib.pyplot as plt
j = arange(0, 101, 2)
plt.plot(E[:,None] - 0.5*j[None,:], dos[:,0,::2] + 0.08*j[None,:], 'k-')
plt.xlabel('$E/E_T$'); plt.ylabel('$n/n_N$')
plt.ylim(0, 15); plt.xlim(-50, 300)
plt.savefig('dos.eps')
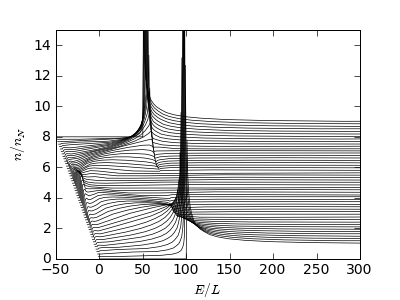
There is the minigap, already reduced by the finite phase difference.
Current-phase relation¶
First, we want to switch to a faster solver:
solver.set_solvers(sp_solver=u.SP_SOLVER_TWPBVP)
The default one is u.SP_SOLVER_COLNEW; there are some cases where
TWPBVP does not converge, so it is not the default.
Current-phase relation can be calculated as follows:
phi = linspace(0, pi, 50)
I_S = zeros([50])
geometry.t_t = 1e-6 # Zero temperature
for j, p in enumerate(phi):
geometry.t_phase = array([-.5, .5]) * p
solver.solve()
Ic, Ie = solver.get_currents(ix=0)
I_S[j] = Ic[0]
savetxt('sns-I_S.dat', c_[phi, I_S])
What we do here is:
loop over different values of phases
change the phase difference in the
geometryobjectsolve the spectral equations for each phase difference
compute the currents in the wire, at grid position 0
save the result to a file as two columns
The result is:
plt.clf()
plt.plot(phi/pi, I_S, 'k-')
plt.xlabel(r'$\varphi/\pi$'); plt.ylabel('$e R_N I_S / E_T$')
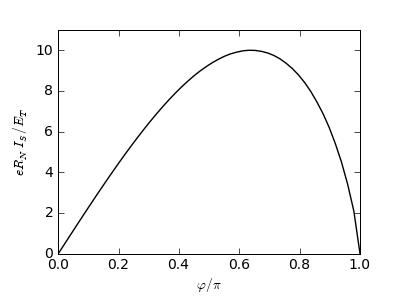
As we had 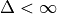 , the maximum
, the maximum 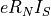 does not reach
does not reach
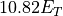 .
.
