PROJEKTIVERKKO

Töiden järjestely muistuttaa sijoitteluongelmaa, haetaan n:lle eri työlle tapa tehdä ne m:n eri vaihtoehdon joukosta. Erotuksena sijoitteluongelmaan on töiden suoritusjärjestyksiin liittyvät ehdot. Töiden järjestelyn eräs sovellusalue on projektisuunnittelu.

Projektisuunnitteluun on tehty erilaisia projektinhallintamenetelmiä, joista tunnetuimpia ovat 50-luvun lopulla kehitetyt CPM (Critical Path Method) ja PERT (Program Evaluation and Review Technique). Nämä menetelmät eroavat selvimmin ajan arvioinnissa. CPM:ssä se on deterministinen eli perustuu ennalta määrättyihin aikoihin kun taas PERT:issä ajan arviointi tapahtuu stokastisesti eli apuna käytetään satunnaislukujakaumia.

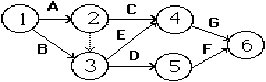
Projektiverkon (*) piirtämisessä on noudatettava eräitä sääntöjä: 1. Verkon jokaisella välillä on suunta (verkko on suunnattu) ja verkolla on aina yksi alku- ja loppusolmu, 2. Välit kuvaavat töitä eli aktiviteetteja, 3. Verkon solmut on numeroitu nousevasti s.e. jokaisen välin päätesolmulla on aina suurempi numero kuin sen lähtösolmulla, 4. Verkko ei saa sisältää silmukoita (eli projekti ei saa jäädä "luuppiin") 5. Jokaisen aktiviteetin kuvaamiseen käytetään ainoastaan yhtä väliä ja jokainen väli esittää ainoastaan yhtä aktiviteettia, 6. Kahden solmun välissä on vain yksi aktiviteetti (suunnattu väli), 7. Jotta verkko voitaisiin piirtää s.e. ehdot 5 ja 6 eivät tulisi rikotuiksi, on verkkoon joskus lisättävä ns. valeaktiviteetteja (dummy activity), joiden kesto on nolla. Esimerkiksi jos työ A edeltää töitä C sekä D ja työ B edeltää myös D:tä, mutta ei C:tä niin verkon piirtäminen onnistuu lisäämällä valetyö A:n päätesolmusta (2) B:n päätesolmuun (3). Katso oheisen esimerkin kuvaa alla. Huom! Jos jollakulla aktiviteetilla ei ole edeltäjää niin sen lähtösolmu on tietenkin solmu nro 1.

Projektin kokonaiskesto saadaan selville kriittisen polun avulla. Kriittisen polun määräämiseksi on tarpeen laskea seuraavia lukuarvoja: varhaisin aloitusaika (ES, earliest start time), myöhäisin aloitusaika (LS, latest start time), varhaisin lopetusaika (EF, earliest finish time), myöhäisin lopetusaika (LF, latest finish time) ja aktiviteetin pelivara (TS,). Nämä arvot voidaan laskea seuraavin yhtälöin kun aktiviteetin kestoa merkitään T:llä: ES(alkusolmusta lähtevä aktiviteetti) = 0, ES(x) = max{EF(x:ää edeltävä aktiviteetti)} eli suurin x:ää edeltävien aktiviteettien varhaisimmasta päättymisajasta, EF(x) = ES(x) + T(x). Projektin aikaisin mahdollinen päättymisaika on EF(n) kun n on viimeinen aktiviteetti. Jatketaan laskemalla takaperin: LF(n) = EF(n), LS(n) = LF(n) - T(n), ..., LF(x) = min{LS((x:ää seuraava aktiviteetti)} eli pienin x:ää seuraavien aktiviteettien myöhäisimmästä alkamisajasta, LS(x) = LF(x) - T(x). Kun verkko on laskettu "läpi" niin saadaan pelivarat yksinkertaisesti: TS(x) = LS(x) - ES(x).

Jos TS(x) = 0 niin aktiviteetti kuuluu projektiverkon kriittiseen polkuun.

Kriittisellä polulla ei siis ole pelivaraa ja vastaavasti ne aktiviteetit, joilla TS>0, on ns. vapaata pelivaraa. Vapaa pelivara on se aika, minkä ko. työ voi myöhästyä vaikuttamatta seuraavan työn alkamiseen.

Esimerkki. On piirrettävä projektiverkko, jossa töiden järjestys on määrätty seuraavasti: Työtä C edeltää työ A, töitä E ja D edeltävät työt A ja B, työtä G edeltävät työt C ja E sekä työtä F edeltää työ D. Tutki missä ajassa projekti on mahdollista viedä läpi kun töiden kestoajat ovat seuraavat: A=3, B=2, C=3, D=5, E=3, F=2 ja G=5.

Lasketaan arvot kullekin aktiviteetille. Esimerkiksi EF(A) = ES(A) + T(A) = 0 +3 = 3,... (lasketaan verkko loppuun), LF(A) = min {LS(C), LS(D), LS(E)} = min{3, 3, 4} = 3, LS(A) = LS(A) - T(A) = 3 - 3 = 0 ja TS(A) = LS(A) - ES(A) = 3 - 3 = 0.

Viimeiseltä sarakkeelta voidaan lukea että kriittiseen polkuun kuuluvat kaikki muut aktiviteetit paitsi B, D ja F, joilla pelivara on suurempi kuin nolla. Mikäli mikään kriittisen polun töistä (aktiviteeteista) ei myöhästy ja muut työt myöhästyvät korkeintaan yhden aikayksikön niin projekti saadaan vietyä läpi 11:ssä aikayksikössä.

(*) Projektiverkon piirtämisessä näkee joskus käytettävän myös tapaa, jossa aktiviteetit merkitään solmuina. Tällä tavoin piirrettyyn verkkoon on edellä annettuja piirtämissääntöjä tietenkin sovellettava toisin.

Demot 9: 3.-5.