Kauppamatkustajan ongelmassa oli tavoitteena löytää verkossa lyhin sellainen polku, joka käy verkon jokaisessa solmussa ainakin kerran ja palaa sitten lähtösolmuun (vertaa kauppamatkustajan ongelmaa ns.
Hamiltonin silmukkaan ¤). Tällainen suljettu polku muodostaa siis verkossa silmukan.Lyhimmän polun ongelmassa ei palata takaisin lähtöpisteeseen vaan tavoitteena on löytää lyhin polku kahden eri solmun välillä. Toinen ero kauppamatkustajan ongelmaan on se että verkon kaikissa solmuissa ei ole tarpeen käydä.

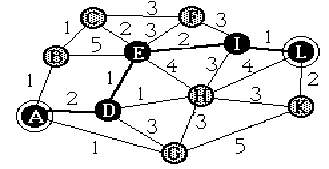
Eräs paljon käytetty tapa hakea verkosta lyhin polku on käyttää Dijkstran algoritmia. Ratkaistaan lyhin polku yllä olevasta verkosta käyttäen Dijkstran algoritmin avulla.
Esitetään ensin verkko ns. etäisyysmatriisina:

Aloitetaan solmusta A merkitsemällä sille pysyvä tunnus (alleviivattu luku), joka on 0. Etäisyysmatriisista katsotaan matka naapurisolmuihin. Vaihtuvista tunnuksista valitaan pienin pysyväksi ja katsotaan jälleen matka etäisyysmatriisista. Jos summa pysyvän tunnuksen arvo ja matka on pienempi kuin vastaavalla solmulla aiemmin ollut vaihtuva tunnus niin summa sijoitetaan vaihtuvaksi tunnukseksi. Valitaan jälleen pienin pysyväksi tunnukseksi ja jatketaan näin loppuun saakka. Täten saadaan lyhimmän polun pituus. Mitä kautta lyhin polku kulkee selviää takaperin laskemalla. Verrataan ensin loppusolmun etäisyyksiä vastaavien pysyvien tunnuksien erotuksiin. Jos ne ovat samat niin solmu kuuluu lyhinpään polkuun. Esimerkiksi loppusolmun L etäisyydet naapurisolmujen joukkoon {H,I,K} ovat {4,1,2} ja vastaavat pysyvien tunnusten erotukset ovat 6-{3,5,6}= {3,1,0}. Vertaamalla joukkoja nähdään että erotus = etäisyys solmun I kohdalla (=1). Tästä seuraa että solmu I kuuluu lyhinpään polkuun. Seuraavaksi tarkastellaan aivan samoin I:n naapurisolmuja ja näin jatketaan solmu solmulta takaisin alkuun. On syytä muistaa että lyhyimpiä polkuja voi olla myös useampia. Katso alla olevaa taulukkoa:
