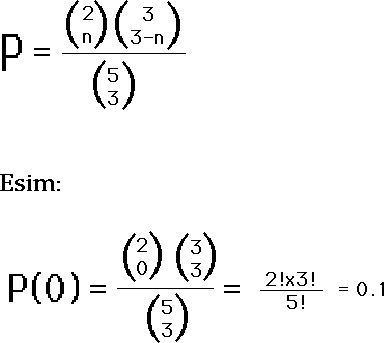
TODENNÄKÖISYYSLASKENNAN ALKEITA JA KOMBINATORIIKKAA
Todennäköisyyslaskenta on varsin erikoinen matematiikan osa-alue ja tämän matematiikan alueen ilmiöiden peruslait on hyvä tuntea koska niiden tietämys auttaa tarkastelemaan realistisemmin yhteiskuntaa sekä maailmankuvaamme. Monet teoreettisen fysiikan tulokset, jotka muovaavat käsitystämme maailmankaikkeudesta, perustuvat todennäköisyyslaskennan lakeihin. Todennäköisyyslaskennan kaavoihin perustuvilla tilastoilla voidaan ihmisten mielipiteitä ohjailla haluttuun suuntaan ja tietämättömyys näistä laeista johtaa myös usein vaikeina aikoina ihmiset hakemaan turvaa erilaisista pseudotieteistä.
Lyhyesti historiasta:
Tärkeänä merkkipaaluna, ehkäpä jopa todennäköisyyslaskennan syntyhetkenä tieteeksi, voidaan pitää vuotta 1657. Tuolloin julkaistiin Ranskassa teos "On Reasoning in Games of Dice" tekijöinä Pascal, Fermat ja Huygens. Siemen kirjan synnylle istutettiin kolme vuotta aikaisemmin kun uhkapeluri Antoine Gombaund Chevalier de Mére esitti ystävälleen Blaise Pascalille erään noppapeliin liittyvän ongelman. Pascal käytti ratkaisussa apunaan ns. aritmeettista kolmiota (tai kombinatorista kolmiota, tai binomiaalista kolmiota), jota sen jälkeen on yleisesti kutsuttu "Pascalin kolmioksi" vaikka se olikin tunnettu jo satoja vuosia ennen Pascalia.
Jos Kleopatran nenä olisi ollut toisennäköinen niin olisi myös maailmanhistoria ollut toisenlainen" (Blaise Pascal)
Eräitä käsitteitä ja perusaksioomia:
- Otosavaruus S. Tapahtuma E on otosavaruuden osajoukko.
- Tapahtuman E todennäköisyyttä merkitään P(E). Jos P(E)=1 niin todennäköisyys on 100%.
- Aina on voimassa: P(E)>=0 ja P(S)=1.
- Jos tapahtumat E1,...,En ovat toisensa pareittain poissulkevia niin P(E1È...ÈEn)=SP(Ek).
- Ehdollinen todennäköisyys P(E1/E2) = P(E1ÇE2)/P(E1).
- Jos P(E1/E2) = P(E1) niin tapahtumat E1 ja E2 ovat riippumattomia (stokastisesti riippumattomia) eli tieto toisen tapahtumisesta ei vaikuta toiseen. Esimerkiksi kolikon heitto (kruuna vai klaava?).
- Satunnaismuuttuja X on funktio, joka liittää luvun otosavaruuden jokaiseen pisteeseen. Satunnaismuuttuja voi olla diskreetti tai jatkuva. Jos se on jatkuva niin on tunnettava sen tiheysfunktio.
HUOM! Joissain vanhemmissa selaimissa (esim. Netscape 3.0) saattavat integraalin ja neliöjuuren merkit näkyä alla kysymysmerkkeinä, tms.- Satunnaismuuttujan odotusarvo eli keskiarvo E(X)= SxkP(X=xk) kun X on diskreetti ja =∫xf(x)dx kun X on jatkuva ja f(x) on sen tiheysfunktio.
- Satunnaismuuttujan varianssi var X= S[xk-E(X)]2P(X=xk) diskreetissä tapauksessa ja
=∫[x-E(X)]2f(x)dx jatkuvassa tapauksessa. X:n keskipoikkeama on √var X.
- Poissonin jakauma f(Xt=n)=P(Xt=n)= e-lt(lt)n/n!, missä l on saapumiset/aika ja Xt on saapumisten määrä aikavälillä [0,t).
Esimerkki:
Vierailet Bagdadin basaarissa, jossa hyväuskoisten rahoja nyhdetään erilaisilla arvaus- ja uhkapeleillä. Yksi tämän alan yrittäjä on Hassan, joka perustaa leipäpuunsa todennäköisyyslaskennan lakeihin. Hassanilla on edessään viisi kannellista koria, joista kolmen sisällä on $10. Kaksi koreista on tyhjiä. Asiakkaalla on mahdollisuus osallistua peliin viiden dollarin panoksella. Rahan annettuaan hän yrittää arvata mitkä kolme koria sisältävät rahan. Onnistuessaan hän saa pitää kaikki rahat, siis $30, mutta mikäli yksikin arvaus menee pieleen niin hän menettää kaikki. Kuinka suuri on voiton todennäköisyys?Ratkaisu: Otosavaruus S on kaikkien valintamahdollisuuksien joukko, mikä on yhtä kuin kaikki ne kombinaatiot, joilla kolmen alkion joukko voidaan erottaa viiden alkion joukosta. Tällaisten kombinaatioiden määrä on 5!/3!(5-3)!= 10. Otosavaruus eli 5!/3!(5-3)! kpl kombinaatioita on alla olevissa laskuissa nimittäjänä (huomioi merkintätapa). Näistä kombinaatioista vain yksi antaa positiivisen tuloksen, joten voiton tn. on 0.1 eli 10%. Ratkaisu voidaan ajatella myös peräkkäisinä valintoina, jolloin se on helpompi hahmottaa. Tällöin ensimmäistä koria valittaessa mahdollisuus löytää sieltä $10 olisi 3/5. Jos ensimmäinen valinta osui oikeaan niin seuraavan korin kohdalla olisi tn. 2/4 ja edelleen, toisenkin ollessa oikein, on kolmannen kohdalla tn. 1/3. Joten koko prosessin todennäköisyydeksi saadaan: 3/5 x 2/4 x 1/3 = 1/10. Jos oletetaan, että avataan kolmen korin kansi siitäkin huolimatta, että on jo kertaalleen erehdytty niin todennäköisyys sille, että valitun kolmen korin joukossa on täsmälleen n tyhjää (n=0,1,2) niin saadaan seuraavasti:
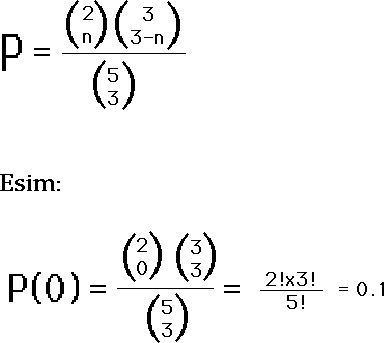
Edellisessä esimerkissä tapaus n = 0 oli siis tapaus, jossa asiakas voitti. On helppo huomata, että Hassan pääsee ajan myötä kasvattamaan yrityksensä pääomaa varsin mukavasti, jos hän häviää mainitut $30 vain keskimäärin, joka kymmenessä pelissä.
Varsin usein kuitenkin tämän tyyppisissä peleissä myös petkutetaan. Oletetaan, että huomaat sattumalta rehdin Hassanin epärehellisen kollegan, Ahmed Ahneen sujauttavan $10 vain kahteen koriin. Miten menettelisit voittaaksesi jos runsaslukuinen, petkutuksesta tietämätön basaariyleisö vaatisi sinua pelaamaan? Mikäli uskallat väittää Ahmedia epärehelliseksi menetät henkesi hurjistuneen väkijoukon toimesta. Samoin kävisi Ahmedille jos hänen petoksensa tulisi ilmi (->VASTAUS). Kysymyksessä ei ole todennäköisyyslasku, mutta tehtävä ehkä sivuaa jollain tavoin kurssin problematiikkaa.
Demot 1: 1.-6., 2: 6.-8. ja 3: 4.