KAUPPAMATKUSTAJAN ONGELMA
TRAVELING SALESMAN PROBLEM
BRANCH-AND-BOUND MENETELMÄ
Jos sijoitusongelma oli kuljetusongelman (joka oli tavallisen LP-ongelman rajatapaus) rajatapaus niin kauppamatkustajan ongelmaa voidaan puolestaan pitää sijoitteluongelman erikoismuotona. Toisaalta verkkoteoriassa tunnettu
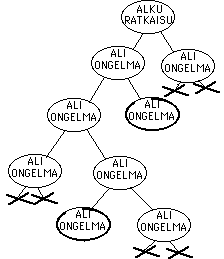
Hamiltonin polku on muistuttaa kauppamatkustajan ongelmaa ollen sen erikoistapaus. Tehtävänä on yksinkertaisesti hakea lyhin reitti joka kiertää verkon kaikkien solmujen kautta palaten lopuksi takaisin lähtösolmuun. Kyseessä voi olla esimerkiksi joukko firmoja, joista jokaisessa kauppamatkustajan on käytävä kertaalleen. Kauppamatkustajan ongelma on eräs matematiikan perinteellisiä "suuria ongelmia", jonka ratkaisemiseksi on kehitetty lukuisa määrä erilaisia algoritmeja. Ja säännöllisin väliajoin joku aina "keksii" sen parhaan menetelmän. Tyypillisesti mm. tätä ongelmaa ratkaistaan branch-and-bound menetelmää käyttäen. Branch-and-bound ("haaroitu ja rajoita") soveltuu monien muidenkin kokonaislukuoptimointitehtävien ratkaisuun (esim. knapsack problem) Ajatuksena on ajatella tehtävää ensin sijoitusongelmana, jolle haetaan ratkaisu (esim. unkarilaista menetelmää käyttäen). Ratkaisu ei kuitenkaan ole yleensä käypä (esimerkiksi koostuu useasta irrallisesta reitistä), jolloin jaetaan ongelma alitehtäviin poistamalla saadusta ratkaisusta kussakin alitehtävässä yksi alkio. Kukin alitehtävistä ratkaistaan jälleen sijoitusongelmana kunnes jossain haarassa saadaan käypä ratkaisu, minkä jälkeen muita haaroja jatketaan niin kauan kuin on mahdollista saavuttaa vielä parempi tulos (ks. oikeanpuoleinen kuva alla).Käsin tehtäviä ratkaisuja varten on kehitetty menetelmän sovellus, joka eliminoi ratkaisuun johtamattomat sivuhaarat jo menetelmän kuluessa. On huomattava, että lopullinen ratkaisu on aina arvoltaan suurempi tai yhtäsuuri kuin ensimmäinen
sijoitusmenetelmällä haettu ratkaisu. Kauppamatkustajan ongelma LP-ongelmaksi muotoiltuna on muutoin aivan samanlainen kuin edellä esitetty sijoitusongelma, mutta lisäksi sen on sisällettävä ns. rengasehto eli alkioista on muodostuttava verkossa yksi yhtenäinen rengas. Alla on ratkaistu pieni 5 solmun verkosta koostuva tehtävä. Matriisissa tapahtuvat toimenpiteet on selitetty seuraavalla sivulla.
1. Käsiratkaisu:

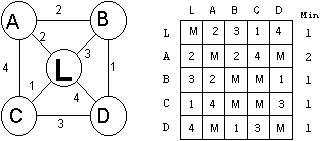
Ongelmaa kuvaava verkko (L on lähtö) ja vastaava etäisyysmatriisi (jos ei väliä niin arvo on M, jokin suuri luku)
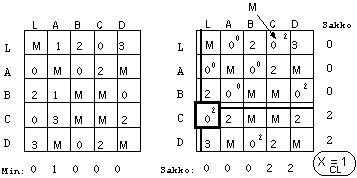
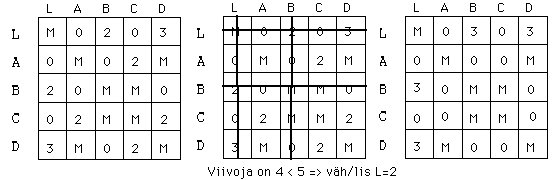
Vähennetään riviminimit ja sarakeminimit. Lasketaan kullekin riville ja sarakkeelle sakko, joka on toiseksi pienimmän alkion (pienin on aina 0) arvo. Kullekin 0-alkiolle annetaan sakko (yläindeksi), joka on Max {rivisakko, sarakesakko}. Suurimman sakon saanut alkio otetaan kantaan (tässä xCL) ja samalla poistetaan matriisista vastaava rivi ja sarake. Käänteisalkio (xLC) eliminoidaan antamalla sille arvoksi M. Näin estetään mahdollisuus palata samaa reittiä takaisin. Samalla tavalla estetään myös pidempien silmukoiden muodostuminen, siis antamalla M sellaisten välien arvoiksi, joita pitkin voitaisiin palata syntyvälle reitille takaisin "liian aikaisin".
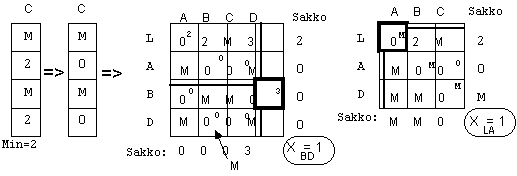
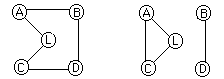
Sarakkeelle C ei jäänyt yhtään nollaa, joten vähennetään sarakeminimi (2) ja jatketaan pienentyneessä matriisissa kuten edellä. Näin jatketaan lisää välejä kantaan ottaen kunnes matriisi on supistunut ollen kokoa 2x2. Otetaan kantaan viimeiset kaksi väliä ja saadaan kauppamatkustajalle reitti, joka on esitetty kuvassa alla. Reitin pituus on 9 ja se voidaan luonnollisesti kiertää kumpaankin suuntaan.
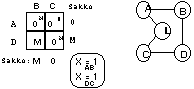
Jos samaa tehtävää lähdetään ratkaisemaan
sijoitusongelmana niin saadaan neljä kantaratkaisua, joista kaksi on matriisin symmetrisyyden vuoksi samoja. Kummankin jäljelle jäävän ratkaisun arvo on 9, mutta toinen ei ole käypä ratkaisu koska reitti ei ole yhtenäinen (oikeanpuoleinen kuva alla). Branch-and-bound menetelmässä ratkaistaisiin seuraavaksi oikeanpuoleista verkkoa vastaava matriisi kolmena eri sijoitusongelmana, joista kussakin on yksi kolmion ACL väleistä eliminoitu antamalla sille matriisissa arvo M. Näin saaduista ratkaisuista jatkuu haarautuminen edelleen alitehtäviin kunnes on saatu rengasehdon täyttävä verkko tai kun ratkaisun (ei välttämättä käypä) arvo on suurempi kuin parhaan jo saadun käyvän ratkaisun. Tässä nimenomaisessa tapauksessa prosessi pysähtyy heti alussa sillä vasemmanpuoleinen verkko on ratkaisuna käypä ja sen arvo on jo vähintään yhtä hyvä kuin mikä menetelmää jatkamalla voitaisiin saavuttaa.