Tehtävä:
Matemaattisesta päättelemisestä
Tässä tehtävässä käydään läpi matemaattiseen päättelyyn liittyviä peruskäsitteitä: (avoin) väite, vastaesimerkki, päättelyimplikaatio, päättelyekvivalenssi, päättelyn asiayhteys, päättelyaskel ja päättelyketju. Tehtävässä korostetaan sitä, että vaikka päättelyssä usein käytetään matemaattisia sääntöjä, pätevän päättelyn erottaa epäpätevästä viime kädessä vain se, onko millekään päättelyaskeleelle olemassa vastaesimerkkiä. Lopuksi käydään läpi ohjelmointia sivuava esimerkki.
Jos käytät MathCheckiä ensimmäistä kertaa, niin tee ensin tehtävä Yleistä MathCheckistä. Jos et muualta löydä miten jokin symboli kirjoitetaan, niin katso MathCheck Brief Instructions.
Väite ja vastaesimerkki
Väite on tässä tehtävässä mikä tahansa, joka tuottaa totuusarvon tosi (T) tai epätosi (F). Laskemme alkajaisiksi väitteen x2 − 2y > x + 1 totuusarvon parissa tilanteessa.
Avoin väite on väite, jossa esiintyy tilanteesta riippuvaa arvoa tarkoittava ilmaus. Sellaista ilmausta sanotaan muuttujaksi. Esimerkiksi ”siellä on yliopisto” on avoin väite, koska ”siellä” on muuttuja. Sehän voi tarkoittaa mitä tahansa paikkakuntaa. Vaikka tietäisimme, mitä ”siellä” tällä kertaa tarkoittaa, se on silti muuttuja.
Suljettu väite on väite, jossa ei esiinny tilanteesta riippuvaa arvoa tarkoittavaa ilmausta. Esimerkiksi ”Jyväskylässä on yliopisto” on suljettu väite.
On tavallista, että avoimen väitteen totuusarvo riippuu muuttujien saamista arvoista. Esimerkiksi x + 1 = 2 on tosi jos x:n arvo on 1, ja epätosi muilla x:n arvoilla. On kuitenkin olemassa myös avoimia väitteitä, joiden totuusarvo ei riipu muuttujien saamista arvoista. Esimerkiksi x + 0 = x on tosi riippumatta siitä, mikä luku laitetaan x:n paikalle.
Vastaesimerkki väitteelle on muuttujien arvoyhdistelmä, jolla väite ei ole tosi. Anna jokaiselle seuraavista vastaesimerkki kirjoittamalla jokaiseen vastausruutuun luku.
Tässä vaiheessa on tarpeen pohtia, mitä tarkoittaa ”muuttujien arvoyhdistelmä”. Ilmaus ”x:n arvo on 2 ja y:n arvo on 5” antaa arvoyhdistelmän kahdelle muuttujalle, nimittäin muuttujille x ja y. Se voidaan esittää kaavana x = 2 ∧ y = 5. Kaava x = 2 ∨ y = 5 ei esitä yhtä arvoyhdistelmää vaan äärettömän monta, muun muassa sellaisen jossa sekä x = 5 että y = 5.
Ilmaus ”x:n arvo on 2” antaa arvoyhdistelmän yhdelle muuttujalle. Ilmaus ”” antaa arvoyhdistelmän nollalle muuttujalle. Arvoyhdistelmää nollalle muuttujalle voi olla hankala ajatella, koska se on tyhjä, mutta se on silti hyödyllinen matemaattinen käsite. Se mm. kelpaa vastaesimerkiksi väitteelle 1 + 1 = 3, sillä 1 + 1 = 3 ei ole tosi silloin kun muuttujilla on ne arvot, jotka tyhjä arvoyhdistelmä määrää.
Kelpaako tyhjä arvoyhdistelmä vastaesimerkiksi väitteelle 1 + 1 = 2? VastausEi kelpaa, sillä 1 + 1 = 2 on tosi silloin kun muuttujilla on ne arvot, jotka tyhjä arvoyhdistelmä määrää.
On tavallista ilmaista matemaattisia lainalaisuuksia avoimina väitteinä, jotka ovat tosia riippumatta muuttujien arvoista. Tässä kaksi tuttua esimerkkiä:
- a(b + c) = ab + ac (kertolaskun osittelulaki)
- (a + b)2 = a2 + 2ab + b2 (binomin neliö)
Päättelyesimerkki: itseisarvoepäyhtälö
Saadaksemme päättelemisen ideasta kiinni aloitamme esimerkillä: millä x:n ja y:n arvoyhdistelmillä pätee |x − y| + x + y < 6?
Itseisarvomerkistä |…| pääsee eroon jakamalla tehtävä kahteen tapaukseen itseisarvon määritelmän mukaan:
|x| =
x , jos x ≥ 0 −x , jos x < 0
Ylempi tapaus
Huomaa äskeisen palautteen alussa ”Assume x ≥ y”. Se tarkoittaa, että vastaesimerkeiksi kelpaavat vain sellaiset x:n ja y:n arvoyhdistelmät, joille pätee x ≥ y. Palaute on siis muodostettu olettaen ylemmän tapauksen jos-ehto.
Tämän ymmärtämiseksi kannattaa kokeilla, mitä tapahtuu, jos tämä oletus poistetaan. Poista edellä ollut valinta, jonka kohdalla luki ”Anna tämän olla aluksi päällä”. Kokeile, minkälaisen palautteen nyt saat edellisestä kohdasta. Onko se asianmukainen palaute itseisarvotehtävän ratkaisemisen kannalta? Open mielipidePalautteessa annetulle vastaesimerkille ei päde x ≥ y. Koska nyt käsitellään tapausta x ≥ y, ei tällainen vastaesimerkki ole asianmukainen, koska se on sen tilanteen ulkopuolella, jota nyt käsitellään. Virhe on samanlainen kuin jos joku antaisi väitteelle ”Kesällä jokaisessa kuukaudessa on 30 tai 31 päivää” vastaesimerkiksi ”helmikuussa on 28 päivää”. Helmikuuhan ei ole kesällä.
Olemme tähän mennessä jakaneet päättelytehtävämme kahteen tapaukseen ja aloittaneet tapauksen x ≥ y käsittelyn muuntamalla alkuperäisen väitteen |x − y| + x + y < 6 muotoon x − y + x + y < 6. Nyt sievennän tämän mahdollisimman yksinkertaiseen muotoon. Havainnollistaakseni mistä päättelyssä on kyse, näytän tavallista enemmän välivaiheita:
| x − y + x + y < 6 | yhteenlaskettavien järjestystä saa vaihtaa | |
| ⇔ | x + x + y − y < 6 | luku miinus sama luku on nolla |
| ⇔ | x + x < 6 | samanmuotoiset termit saa yhdistää |
| ⇔ | 2x < 6 | epäyhtälön molemmat puolet saa jakaa samalla positiivisella luvulla |
| ⇔ | x < 3 |
Alempi tapaus
Tapausten yhdistäminen
Kun päättely jaetaan tapauksiin, niin tapausten lopputulokset yhdistetään tällä periaatteella:
tapauksen 1 ehto ja tapauksen 1 tulos tai tapauksen 2 ehto ja tapauksen 2 tulos tai tapauksen 3 ehto ja tapauksen 3 tulos tai tapauksen 4 ehto ja tapauksen 4 tulos
Jatka samaan malliin
Nyt tehtäväsi on ratkaista |2a + b − 9| + b ≥ 2a + 1 edellä kuvatulla tavalla. Jokaisessa kohdassa on tarkoitus, että ensin muokkaat vastauksen muotoon jossa ei tule muuta kuin kompleksisuusilmoitus, ja sen jälkeen muokkaat sen tarpeeksi lyhyeen muotoon yhdellä tai useammalla välivaiheella. Jätä välivaiheitasi näkyviin ja erota ne toisistaan symbolilla <=>.
Päättelyoperaattorit
Olet edellä kirjoittanut symbolin ⇔ tai sen ASCII-vastineen <=>. Sitä kutsutaan nimillä looginen ekvivalenssi, päättelyekvivalenssi tai lyhyesti ekvivalenssi. Sana ”ekvivalenssi” tarkoittaa monia muitakin matemaattisia käsitteitä mukaan lukien tavallinen yhtäsuuruus =, joten voi syntyä sekaannuksen vaara. Se vältetään käyttämällä etuliitettä ”looginen” tai ”päättely”.
Etuliite ”päättely” korostaa symbolin ⇔ eroa symboliin ↔: ↔ esiintyy väitteiden sisällä, tuottaa totuusarvon F tai T (kolmiarvologiikassa myös U), eikä riipu asiayhteydestä vaan ainoastaan vasemman ja oikean puolensa tuottamista totuusarvoista. Symboli ⇔ esiintyy väitteiden välissä, ei tuota totuusarvoa vaan tuloksen ”pätevä päättelyaskel” tai ”ei pätevä päättelyaskel”, ja riippuu asiayhteydestä. Alamme nyt käsitellä tätä perusteellisesti.
Vasen ⇔ oikea tarkoittaa, että kaikilla niillä asiayhteyden sallimilla muuttujien arvoyhdistelmillä, joilla vasen puoli on tosi, myös oikea puoli on tosi, ja päinvastoin.
Vastaesimerkki tälle on sellainen muuttujien arvoyhdistelmä, jonka asiayhteys sallii ja jolla toinen puoli on tosi, mutta toinen puoli ei ole tosi.
Otetaan ensin tapauksia, joissa asiayhteys sallii kaikki muuttujien arvoyhdistelmät. Kirjoita vastaesimerkki tai valitse ”ei vastaesimerkkejä”.
Yksi esimerkki asiayhteydestä on edellä olleet assume-osat. Kun sievensimme |x − y| + x + y < 6 ⇔ x − y + x + y < 6 , niin MathCheck hyväksyi sen kun assume x ≥ y oli päällä, mutta antoi vastaesimerkin kun se ei ollut päällä.
Tässä esimerkissä, kun assume x ≥ y on pois päältä, asiayhteys salli kaikki x:n ja y:n arvoyhdistelmät. Silloin esimerkiksi x = 2 ja y = 3 on pätevä vastaesimerkki päättelyaskeleelle |x − y| + x + y < 6 ⇔ x − y + x + y < 6 . Vasen puoli tuottaa 6 < 6 joka ei ole tosi; ja oikea puoli tuottaa 4 < 6 joka on tosi.
Tässä esimerkissä, kun assume x ≥ y on päällä, asiayhteys ei salli vastaesimerkiksi x = 2 ja y = 3, koska x ≥ y ei päde sille. Itse asiassa silloin mikään ei ole pätevä vastaesimerkki, koska silloin itseisarvon määritelmän mukaan |x − y| = x − y, joten vasen ja oikea puoli ovat samanlaiset.
Asiayhteys voi koostua useasta osasta. Matemaattisissa teksteissä asiayhteyden kertomiseen saatetaan käyttää sekä sanoja että kaavoja, ja ne voivat olla jakaantuneet useaan osaan jotka saattavat sijaita kaukana toisistaan. Käytettävä lukutyyppi saatetaan sanoa kirjan alussa tai jättää kokonaan sanomatta. Kuitenkin sillä on tärkeä merkitys. Kummallekin alla olevista vaihtoehdoista, mieti ensin itse miten asia on, ja sitten kokeile mitä mieltä MathCheck on asiasta.
Harjoittelemme asiayhteyden vaikutusta.
MathCheckin antamassa palautteessa on esiintynyt myös ⇐. Olet saattanut nähdä symbolin ⇒, joka tunnetaan nimellä implikaatio tai päättelyimplikaatio. Nyt on aika kertoa, mitä ne tarkoittavat.
Vasen ⇒ oikea tarkoittaa, että kaikilla niillä asiayhteyden sallimilla muuttujien arvoyhdistelmillä, joilla vasen puoli on tosi, myös oikea puoli on tosi.
Vastaesimerkki implikaatiolle on sellainen muuttujien arvoyhdistelmä, jonka asiayhteys sallii ja jolla vasen puoli on tosi, mutta oikea puoli ei ole tosi.
Symbolin ⇐ merkitys on helppo arvata: se on ⇒ takaperin.
Vasen ⇐ oikea tarkoittaa samaa kuin oikea ⇒ vasen.
Käykäämme läpi kaikki edellä olleet tapaukset, joissa on vastaesimerkkejä, ja selvittäkäämme, kummin päin niihin on vastaesimerkkejä (tai jopa molemmin päin). Kaikki luvut ovat reaalilukuja.
Päättelyoperaattoreiden käyttö luetaan usein sanallisesti seuraavasti:
ilmaus voidaan lukea vasen ⇔ oikea vasen jos ja vain jos oikea vasen ⇒ oikea jos vasen niin oikea vasen ⇐ oikea vain jos vasen niin oikea
Toisinpäin, nämä sanalliset ilmaukset tarkoittavat yleensä samaa kuin vastaavat päättelyoperaattorit, sovellettuna siihen käsitemaailmaan josta kulloinkin on puhe. Sanallisissa ilmauksissa myös vasen ja oikea voivat olla sanallisia. Ne voivat puhua paitsi kohdemaailmasta myös esimerkiksi logiikan käyttöön liittyvistä asioista, kuten esimerkissä ”päättelyaskel on epäpätevä jos ja vain jos sille on vastaesimerkki”.
Matematiikassa käytetään toisinaan myös seuraavia ilmauksia vastaten päättelyoperaattoreita, nekin sovellettuna siihen käsitemaailmaan josta on puhe:
ilmaus voidaan lukea vasen ⇔ oikea vasen on välttämätön ja riittävä ehto oikea:lle vasen ⇒ oikea vasen on riittävä ehto oikea:lle vasen ⇐ oikea vasen on välttämätön ehto oikea:lle
Alimmaisen takana oleva ajatus on, että on mahdotonta että oikea pätee mutta vasen ei päde, siksi vasen on välttämätön ehto. Keskimmäisessä vasen riittää takaamaan että oikea pätee, mutta oikea voi päteä myös vaikka vasen ei pätisi, joten vasen ei ole välttämätön.
Päättelyaskel ja päättelyketju
Ilmaukset muotoa vasen ⇒ oikea, vasen ⇐ oikea ja vasen ⇔ oikea ovat päättelyaskelia. Päättelyaskel ei tuota totuusarvoa, vaan on pätevä tai epäpätevä. Se on epäpätevä jos ja vain jos sille on vastaesimerkki.
Päättelyaskeleen pätevyys ei siis määräydy siitä, onko se perusteltavissa jollakin matemaattisella säännöllä. Päättelyaskeleen pätevyys määräytyy vain ja ainoastaan siitä, onko sille vastaesimerkkiä.
Toisaalta hyvin usein on vaikea selvittää, onko päättelyaskeleelle vastaesimerkkiä. Siksi yleensä käytännössä vaaditaan, että kukin päättelyaskel pitää voida perustella jollakin matemaattisella säännöllä, josta tiedetään, että se tuottaa vain päteviä päättelyaskelia. Niinpä matemaattiset säännöt ovat käytännössä välttämättömiä päättelylle, vaikka ne eivät pohjimmiltaan olekaan pätevyyden kriteeri.
Jos alla vasen ⇐ oikea on pätevä, niin valitse vasemmanpuoleinen ruutu. Jos vasen ⇔ oikea on pätevä, niin valitse keskimmäinen ruutu. Jos vasen ⇒ oikea on pätevä, niin valitse oikeanpuoleinen ruutu.
Viimeisin edellä olleista kohdista tuo esiin sen, että päättelytilanteissa voi esiintyä määrittelemättömiä väitteitä. Päättelyaskel ei kuitenkaan voi olla määrittelemätön. Jos tehtävänä on selvittää, mitkä luvut toteuttavat yhtälön 3 √x + 2 = x + 4, niin ei ole epäselvää eikä määrittelemätöntä, toteuttaako x = −3 sen: ei toteuta. Päättelyaskel
3 √x + 2 = x + 4 ⇔ x = −1 ∨ x = 2
on pätevä siitä huolimatta, että kun x = −3, niin sen vasen puoli on määrittelemätön. (Toisinaan esiintyvä näkemys, että ym. päättelyaskeleessa tarkastellaan vain niitä lukuja joilla molemmat puolet on määritelty, kaatuu mm. siihen, että tehtävänanto ei tyypillisesti ole muotoa ”ratkaise tämä yhtälö olettaen, että x ≥ −2” vaan ”ratkaise tämä yhtälö”.)
Siis väite voi saada kolme eri totuusarvoa: tosi, epätosi ja määrittelemätön, mutta päättelyaskeleella on vain kaksi mahdollisuutta: se on tai ei ole pätevä. Harjoittelemme tätä seuraavalla esimerkillä:
x > 0 ⇔> 0
1 x
Onko esimerkin päättelyaskel pätevä? VastausKun olet saanut taulukon täytettyä oikein, niin siinä ei ole yhtään riviä, jossa toisella puolella on T mutta toisella puolella on F tai U. Toisin sanoen, kaikilla niillä asiayhteyden sallimilla muuttujien arvoyhdistelmillä, joilla vasen puoli on tosi, myös oikea puoli on tosi, ja päinvastoin. Se täsmää symbolille ⇔ edellä annettuun määritelmään. Esimerkin päättelyaskel on siis pätevä.
Ehkä huomasit MathCheckin palautteessa symbolin ≡. Se ei kuulu tämän tehtävän oppimistavoitteisiin, mutta siltä varalta että asia kiinnostaa: se on MathCheckin oma päättelyoperaattori, jolle vasen ≡ oikea on pätevä jos ja vain jos jokaisella asiayhteyden sallimalla muuttujien arvoyhdistelmällä vasen ja oikea puoli tuottavat saman totuusarvon. Niinpä F ≡ U ei ole pätevä, vaikka F ⇔ U on pätevä. Samaa symbolia käytetään matematiikassa monessa muussakin merkityksessä, mutta MathCheckissä sitä käytetään näin.
Päättelyaskelista voi muodostaa päättelyketjuja. Päättelyketju vasen ⇒ keskimmäinen ⇒ oikea on pätevä jos ja vain jos sekä vasen ⇒ keskimmäinen on pätevä että keskimmäinen ⇒ oikea on pätevä.
Onko seuraava päättelyketju pätevä? Miksi?
x = −2 ⇒ x ≤ 3 ⇒ x2 ≤ 9
VastausEi ole, koska jälkimmäinen päättelyaskel ei ole pätevä. Esimerkiksi x = −4 on sille vastaesimerkki.
Onko seuraava päättelyketju pätevä? Miksi?
x = −2 ⇒ x = 3 ∨ x = −2 ⇒ x2 ≤ 9
VastausOn pätevä. Ensimmäisen implikaation vasen puoli on tosi ainoastaan silloin kun x = −2. Silloin oikea puoli eli x = 3 ∨ x = −2 tuottaa F ∨ T, joka on T. Toisen implikaation vasen puoli on tosi ainoastaan silloin kun x = −2 tai x = 3. Silloin x2 = 4 tai x2 = 9. Molemmissa tapauksissa x2 ≤ 9, joten oikea puoli on tosi.
Seuraava päättelyketju on klassikko. Mikä sen päättelyaskelista ei ole pätevä? Miksi? VihjeValitse jotkin helpot luvut a:ksi ja b:ksi, ja kokeile väite kerrallaan onko se tosi.
Jos oletetaan a = b ≠ 0, niin a = b ⇒ a2 = ab ⇒ a2 − b2 = ab − b2 ⇒ (a + b)(a − b) = b(a − b) ⇒ a + b = b ⇒ 2b = b ⇒ 2 = 1 .
Vastaus(a + b)(a − b) = b(a − b) ⇒ a + b = b ei ole pätevä, koska jos esimerkiksi a = b = 1, niin sen vasen puoli tuottaa 0 = 0 joka on tosi, mutta oikea puoli tuottaa 2 = 1 joka on epätosi. Virhe voidaan tulkita koulumatematiikan laskusääntöjen kannalta seuraavasti: päättelyaskeleessa molemmat puolet jaetaan luvulla a − b, joka on 0 koska a = b. Mutta nollallahan ei saa jakaa.
Onko seuraava päättelyketju pätevä? Miksi?
√x = x − 2 ⇔ (√x)2 = (x − 2)2 ⇔ x = x2 − 4x + 4 ⇔ 0 = (x − 4)x − (x − 4) ⇔ (x − 4)(x − 1) = 0 ⇔ x = 4 ∨ x = 1
VastausEi ole, koska ensimmäinen päättelyaskel ei ole pätevä. Kun x = 1, niin sen vasen puoli on 1 = −1 joka ei ole tosi, mutta oikea puoli on 1 = 1 joka on tosi.
Onko seuraava päättelyketju pätevä? Miksi?
√x = x − 2 ⇒ (√x)2 = (x − 2)2 ⇔ x = x2 − 4x + 4 ⇔ 0 = (x − 4)x − (x − 4) ⇔ (x − 4)(x − 1) = 0 ⇔ x = 4 ∨ x = 1
VastausOn pätevä.
Ensimmäinen askel on pätevä siksi, että aina kun yhtäsuurille olennoille
tehdään sama, määritelty asia, niin myös lopputulokset ovat yhtäsuuret.
Neliöön korottaminen on aina määritelty.
Vastakkaisen suunnan ei tarvitse päteä, koska ensimmäinen askel käyttää ⇒
eikä ⇔.
Loppu perustuu tuttuihin ja turvallisiin koulumatematiikan sääntöihin lukuun
ottamatta sitä, mitä tapahtuu toisessa askeleessa kun x < 0.
Silloin toinen väite tuottaa U ja kolmas väite tuottaa F, koska
sen vasen puoli on negatiivinen mutta, kuten kohta nähdään, oikea puoli ei
ole: x2 − 4x + 4 = (x − 2)2 ≥ 0, koska
jokaisen reaaliluvun neliö on vähintään 0.
Huomaamme, että ei pelkästään ⇔, vaan myös ⇒ on käyttökelpoinen yhtälöiden ratkaisemisessa. Sen käyttö voi tuottaa ylimääräisiä vastauskandidaatteja, mutta ne voi karsia kokeilemalla kaikki saadut kandidaatit alkuperäisessä yhtälössä.
Onko seuraava päättelyketju pätevä? Miksi?
x + 1 + 2√x = 0 ⇔ x + 1 = −2√x ⇒ (x + 1)2 = (−2√x)2 ⇔ x2 + 2x + 1 = 4x ⇔ x2 − 2x + 1 = 0 ⇔ (x − 1)2 = 0 ⇔ x = 1
VastausOn pätevä. Toisessa askeleessa molemmat puolet korotetaan neliöön, ja neliöinti on aina määritelty. Vastakkaisen suunnan ei tarvitse päteä, koska toinen askel käyttää ⇒ eikä ⇔. Kolmannessa askeleessa negatiiviset luvut tuottavat vasemmalla puolen U ja oikealla puolen F, koska niillä 4x < 0 mutta x2 + 2x + 1 = (x + 1)2 ≥ 0. Muu on tuttua ja turvallista koulumatematiikkaa.
Huomaamme, että äskeinen yhtälö on mahdoton. Sen olisi voinut huomata myös siten, että jotta se voisi toteutua, √x:n täytyy olla määritelty. Siitä seuraa x ≥ 0. Koska neliöjuuret ovat aina ei-negatiivisia, siitä seuraa että x + 1 + 2√x ≥ 0 + 1 + 2 ⋅ 0 = 1 > 0.
Johdimme siis äsken mahdoton ⇒ x = 1 käyttäen vain päteviä matematiikan sääntöjä, ja käyttäen niitä oikein. Kuitenkin perimmäinen kriteeri sille, onko päättelyaskel epäpätevä, on onko sille vastaesimerkkiä. Onko tälle päättelyaskeleelle vastaesimerkkiä? Jos ei, niin miksi ei ole? VastausVastaesimerkki implikaatiolle on muuttujien arvoyhdistelmä, jolla vasen puoli pätee mutta oikea puoli ei päde. Tässä tapauksessa vasen puoli ei päde millään muuttujien arvoyhdistelmällä, joten vastaesimerkkejä ei ole.
Itse asiassa jokainen ⇒-päättelyaskel, jonka vasen puoli on mahdoton, on pätevä. Oikea puoli saa olla ihan mitä tahansa. Millekään niistä ei ole vastaesimerkkiä, koska minkään niistä vasen puoli ei toteudu milloinkaan. Näin täytyy olla monesta syystä, muun muassa siksi, että päättelyä aloitettaessa ei välttämättä tiedetä onko lähtökohta mahdoton, mutta silti täytyy voida päätellä. Tilanne oli juuri tämä yhtälön x + 1 + 2√x = 0 tapauksessa (paitsi jos näit jo alussa, että se on mahdoton yhtälö).
Ihmisten intuitio on toisinaan väärässä. Matemaattisten päättelyjen tapauksessa, jos jokin asia epäilyttää, kannattaa miettiä miltä se näyttää vastaesimerkkien näkökulmasta. Jos päättelylle on vastaesimerkki, niin se on epäpätevä. Jos on varmaa että vastaesimerkkejä ei ole, niin päättely on pätevä vaikka se tuntuisi kuinka hullulta.
Jääkiekon maailmanmestaruuskisoissa oli 4.6.2021 jäljellä neljä joukkuetta. Myös otteluita oli jäljellä neljä: 5.6. Yhdysvallat–Kanada ja Suomi–Saksa sekä 6.6. pronssiottelu ja loppuottelu. Jokaisessa ottelussa on voittaja ja häviäjä (tasapelejä ei ole). Loppuottelussa pelaavat 5.6. ottelujen voittajat. Loppuottelun voittaja saa kultamitalin ja häviäjä hopeamitalin. Pronssiottelussa pelaavat 5.6. ottelujen häviäjät. Pronssiottelun voittaja saa pronssimitalin ja häviäjä ei saa mitään mitalia. Olemme varmaan kaikki samaa mieltä, että tilanne oli sellainen, että jos Suomi voittaa vielä yhdenkin ottelun, niin Suomi saa mitalin.
Mutta ottakaamme tarkasteltavaksi tilanne 6.6. klo 20. Silloin pronssiottelu oli pelattu, mutta loppuottelua ei vielä. Pronssiottelun voitti Yhdysvallat ja hävisi Saksa. Pätikö sillä hetkellä, että jos Suomi voittaa vielä yhdenkin ottelun, niin Suomi saa mitalin? VastausKyllä päti. Suomella oli jäljellä enää yksi ottelu eli loppuottelu. Jos Suomi olisi voittanut sen niin Suomi olisi saanut kultaa. (Suomi hävisi sen ja sai hopeaa.)
Pätikö sillä hetkellä, että jos Saksa voittaa vielä yhdenkin
ottelun, niin Saksa saa mitalin?
Mieti tarkkaan!
Älä anna vaistosi johdattaa sinua harhaan!
VastausKyllä päti.
Vastaesimerkki väitteelle olisi tuolla hetkellä mahdollinen tulevaisuus, jossa
Saksa voittaa vielä jonkin ottelun mutta jää silti ilman mitalia.
Saksa ei kuitenkaan enää voinut voittaa yhtään ottelua, koska sillä ei ollut
jäljellä enää yhtään ottelua.
Niinpä vastaesimerkkejä ei voinut olla, joten väite päti.
”Saksa voittaa vielä jonkin ottelun” oli tuona hetkenä mahdoton, ja
mahdottomasta seuraa mitä tahansa.
”Mitä tahansa” voi olla vaikka ”1 + 1 = 3”, ja se voi olla ”Saksa saa mitalin”.
Tuona hetkenä päti siis sekä ”jos Saksa voittaa vielä yhdenkin ottelun, niin
1 + 1 = 3” että ”jos Saksa voittaa vielä yhdenkin ottelun, niin Saksa saa
mitalin”.
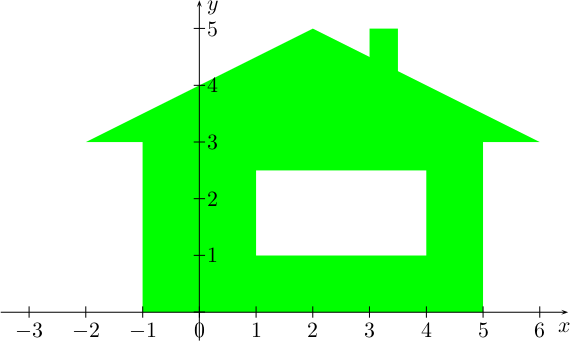
Eräässä tehtävässä opiskelijoita pyydettiin kirjoittamaan kaava, joka esittää oheisen kuvan savupiippua. Jokainen sellainen savupiippu kelpaa, jota rajoittaa neljä suoraa viivaa, ja joka yltää alhaalla niin pitkälle että sen ja katon väliin ei jää pienintäkään rakoa, mutta ei niin pitkälle että sen alareuna alkaa näkyä ikkunasta. Kaikki reunaviivat ovat mukana vihreässä alueessa.
Nyt sinua ei pyydetä kirjoittamaan savupiipun kaavaa, vaan kaavat, joiden
avulla voi tarkastaa, onko annettu savupiipun kaava oikein.
Kirjoita sellaiset kaavat vasen ja oikea, että savupiippu
on oikea vastaus jos ja vain jos vasen ⇒ savupiippu ⇒
oikea.
Vihje 1Mikä on mahdollisimman suuri
sellainen alue ainakin, että laillisen savupiipun pitää peittää ainakin
se?
Vihje 2Miten symbolin ⇒ ja kaavojen
savupiippu ja ainakin avulla ilmaistaan, että savupiipun pitää
peittää ainakin kaavan ainakin ilmaisema alue?
Vihje 3Mikä on mahdollisimman pieni
sellainen alue enintään, että laillinen savupiippu ei saa peittää
yhtään enempää?
Miten symbolin ⇒ ja kaavojen savupiippu ja enintään avulla
ilmaistaan, että savupiippu ei saa peittää liikaa?
Vihje 4Laillinen savupiippu peittää
ainakin kuvassa näkyvän tummanvihreän alueen ja enintään tumman- ja
vaaleanvihreät alueet.
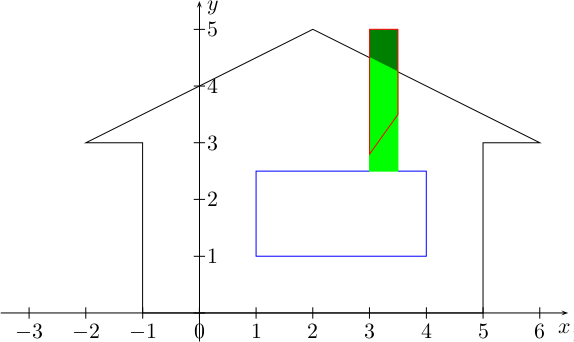
Kuvaan on punaisella piirretty erään laillisen savupiipun reuna.
Päättelyesimerkki: algoritmi parin summalle
Matematiikassa ja tietojenkäsittelytieteessä joudutaan usein perustelemaan, että jokin väite pätee jos ja vain jos jokin toinen väite pätee. Jos merkitsemme näitä väitteitä vasen ja oikea, niin on perusteltava, että vasen ⇔ oikea. Toisinaan tällaisen päättelyn voi viedä läpi pelkästään ⇔-askelilla. Usein kuitenkin joudutaan päättelemään erikseen vasen ⇒ oikea ja erikseen oikea ⇒ vasen. Käymme nyt läpi esimerkin tästä.
Esimerkissä tarkastellaan vähätöistä keinoa selvittää, onko annetuissa luvuissa kaksi, joiden summa on 100. Sanomme tällaisia lukuja satapariksi. Esimerkiksi 36 ja 64 on lukujen 80 36 50 64 12 satapari, mutta 36 ja 50 ei ole, koska 36 + 50 ≠ 100, ja 20 ja 80 ei ole, koska 20 ei ole niissä luvuissa mukana. Sama luku saa olla sataparin molempi luku jos ja vain jos se esiintyy syötteessä ainakin kahdesti. Siksi 50 ja 50 ei ole lukujen 80 36 50 64 12 satapari, mutta on lukujen 50 36 50 64 12 satapari.
Kokeile hetken aikaa, löydätkö näistä luvuista sataparin, mutta jos et löydä, niin älä jatka kauaa:
75 82 96 45 66 85 87 43 75 60 80 78 81 54 82 87 53 28 52 47 42 87 82 42 26
Kokeile hetken aikaa, löydätkö näistä luvuista sataparin, mutta jos et löydä, niin älä jatka kauaa:
67 31 12 53 72 90 42 31 70 97 18 91 45 99 42 74 62 99 86 35 98 91 40 68 29
Oletetaan, että lukujonossa ei ole sataparia. Jos tehtävä ratkaistaan kokeilemalla kaikki parit, jotka lukujonon luvuista voi muodostaa, niin kuinka monta paria pitää kokeilla, jos lukuja on rivin alussa ilmoitettu määrä? Samaa paria (esim. 75 ja 82) ei kokeilla molempiin suuntiin (siis lasketaan joko 75 + 82 tai 82 + 75, mutta ei molempia). Vihje: jos et keksi yleistä lauseketta, tee muutama ensimmäinen kohta tästä tehtävästä.
Tehtävän voi ratkaista paljon vähemmällä työllä seuraavasti. Kutsumme tätä tapaa päistä keskelle -algoritmiksi. Ensin luvut järjestetään kasvavaan suuruusjärjestykseen (se onnistuu paljon vähemmällä työllä kuin kaikkien parien kokeilu):
26 28 42 42 43 45 47 52 53 54 60 66 75 75 78 80 81 82 82 82 85 87 87 87 96
12 18 29 31 31 35 40 42 42 45 53 62 67 68 70 72 74 86 90 91 91 97 98 99 99
Sitten toimitaan seuraavasti:
- Laita vasen etusormi ensimmäisen ja oikea etusormi viimeisen luvun kohdalle.
- Jos etusormet ovat samassa kohdassa, niin lopeta. Sataparia ei ole olemassa. Muutoin jatka kohtaan 3.
- Laske etusormien osoittamien lukujen summa.
3.1 Jos se on pienempi kuin 100, niin siirrä vasenta etusormea yhden luvun verran oikealle ja palaa kohtaan 2.
3.2 Jos se on suurempi kuin 100, niin siirrä oikeaa etusormea yhden luvun verran vasemmalle ja palaa kohtaan 2.
3.3 Jos se on tasan 100, niin lopeta. Satapari on löytynyt.
Yllä oleva algoritmi avautuu toiseen välilehteen tai ikkunaan tästä.
Oletetaan, että lukujonossa ei ole sataparia. Jos tehtävä ratkaistaan päistä keskelle -algoritmilla, niin kuinka monta paria pitää kokeilla, jos lukuja on rivin alussa ilmoitettu määrä?
Seuraavaksi perustelemme, että päistä keskelle -algoritmi tuottaa oikean vastauksen. On todistettava seuraava:
Lukujonossa on satapari ⇔ päistä keskelle -algoritmi löytää sataparin
Suunta oikea ⇒ vasen on tällä kertaa jo lähtökohtaisesti selvä: jos algoritmi on löytänyt lukujonosta sataparin, niin totta kai lukujonossa on ainakin se satapari, jonka algoritmi löysi. Matemaatikot sanovat lähtökohtaisesti selviä tapauksia triviaaleiksi.
Suunta vasen ⇒ oikea vaatii enemmän työtä. Kutsumme seuraavaa väitettä nimellä invariantti. Osoitamme, että se on tosi päistä keskelle -algoritmin kohdan 1 jälkeen, algoritmin loppuun saakka:
Mikään luku vasemman etusormen vasemmalla puolella ei ole sataparin osapuoli. Mikään luku oikean etusormen oikealla puolella ei ole sataparin osapuoli.
Miksi se on tosi kun kohta 1 on suoritettu mutta kohtaa 2 ei ole vielä aloitettu? VastausKohdan 1 jäljiltä vasen etusormi on ensimmäisen luvun kohdalla, joten sen vasemmalla puolella ei ole lukuja. Siksi mikään luku vasemman etusormen vasemmalla puolella ei ole sataparin osapuoli. Vastaavasti oikea etusormi on oikeanpuolimmaisimman luvun kohdalla. Sen oikealla puolella ei ole mitään lukuja, eikä niin ollen myöskään sataparin osapuolena olevia lukuja. Asiaa voi ajatella myös vastaesimerkkien kautta näinJos väite ei päde, niin sille on olemassa vastaesimerkki. Vastaesimerkiksi invariantillemme kelpaa vain sataparin osapuoli, joka on vasemman etusormen vasemmalla puolella tai oikean etusormen oikealla puolella. Mutta niissä paikoissa ei vielä ole lukuja lainkaan. Siksi vastaesimerkkejä ei ole, eli invariantti pätee..
Seuraavaksi on osoitettava, että mikään, mikä tehdään kohdassa 2 tai 3, ei voi saattaa invarianttia pois voimasta. Kohdat 2 ja 3 eivät muuta lukuja eivätkä niiden sijainteja. Mikä on ainoa invariantin kannalta olennainen asia, mitä kohdat 2 ja 3 muuttavat? VastausEtusormien sijainnit.
Siksi tutkimme jokaisen toimenpiteen kohdissa 2 ja 3, joka muuttaa etusormen paikkaa. Voimme keskittyä siihen kun invariantti ensimmäisen kerran lakkaa olemasta voimassa, sillä jos onnistumme osoittamaan että ensimmäistä kertaa ei ole, niin ei voi olla toista eikä kolmattakaan kertaa. Ennen kuin invariantti rikkoutuu ensimmäisen kerran, se on voimassa. Siksi voimme olettaa, että invariantti oli voimassa juuri ennen toimenpidettä. Tehtävämme on osoittaa, että se on voimassa myös välittömästi toimenpiteen jälkeen.
Kun vasenta etusormea siirretään, niin sen vasemmalle puolelle jää luku v, joka ei aikaisemmin ollut sen vasemmalla puolella. Meidän on osoitettava, että v ei voi olla sataparin osapuoli. Jaamme tämän päättelyn kolmeen tapaukseen.
- Miksi v ei voi muodostaa sataparia oikean etusormen kohdalla olevan luvun o kanssa? VastausVasenta etusormea siirretään kohdassa 3.1 (eikä missään muualla). Juuri ennen siirtoa vasen etusormi oli v:n kohdalla. Silloin todettiin, että sen ja oikean etusormen kohdalla olevien lukujen summa on alle 100. Siis v + o < 100, joten ei voi päteä v + o = 100.
- Miksi v ei voi muodostaa sataparia minkään oikeasta etusormesta vasemmalle olevan luvun kanssa? VastausOlkoon x mikä tahansa luku oikeasta etusormesta vasemmalle. Koska luvut ovat kasvavassa suuruusjärjestyksessä, x ≤ o. Siksi v + x ≤ v + o. Edellä nähtiin että v + o < 100, joten v + x < 100.
- Miksi v ei voi muodostaa sataparia minkään oikeasta etusormesta oikealle olevan luvun kanssa? VastausEdellä perusteltiin, että voimme olettaa, että invariantti oli voimassa juuri ennen vasemman etusormen siirtämistä. Invariantin mukaan mikään oikeasta etusormesta oikealle olevista luvuista ei voi muodostaa sataparia minkään luvun kanssa. Niinpä v ei voi muodostaa sataparia minkään niistä kanssa.
Nyt kaikki luvut on tutkittu ja todettu, että v ei voi muodostaa sataparia minkään niistä kanssa.
Myös on osoitettava, että kun oikeaa etusormea siirretään, niin sen kohdalla juuri ennen siirtoa ollut luku o ei voi olla minkään sataparin osapuoli. Matemaatikko saattaisi tyytyä toteamaan, että tilanne on symmetrinen, joten samanlainen päättely toimii kuin vasemman etusormen tapauksessa.
On kuitenkin hyvää harjoitusta tehdä päättely uudelleen sovellettuna oikeaan etusormeen. Tee se! Kiinnitä erityistä huomiota niihin kohtiin, jotka ovat erilaiset kuin äsken. Voit tiivistää vastausta verrattuna vasemman etusormen päättelyyn, kunhan säilytät olennaiset syyt, miksi invariantti säilyy voimassa. Osa 1Luku o ei voi muodostaa sataparia vasemman etusormen kohdalla olevan luvun v kanssa, koska juuri ennen siirtoa todettiin, että v + o > 100, joten v + o ≠ 100. Osa 2Luku o ei voi muodostaa sataparia minkään vasemmasta etusormesta oikealle olevan luvun x kanssa, koska luvut ovat kasvavassa suuruusjärjestyksessä, joten x ≥ v ja siksi x + o ≥ v + o > 100, joten x + o ≠ 100. Osa 3Luku o ei voi muodostaa sataparia minkään vasemmasta etusormesta vasemmalle olevan luvun kanssa, koska invariantti oli voimassa juuri ennen oikean etusormen siirtämistä, ja invariantin mukaan mikään vasemmasta etusormesta vasemmalle olevista luvuista ei voi muodostaa sataparia minkään luvun kanssa. Osa 4Nyt kaikki luvut on tutkittu ja todettu, että o ei voi muodostaa sataparia minkään niistä kanssa.
Olemme osoittaneet, että mikään etusormen siirto ei voi saada invarianttia pois voimasta. Totesimme jo aiemmin, että mikään muukaan, mitä algoritmi tekee, ei voi saada invarianttia pois voimasta. Siksi invariantti on voimassa algoritmin lopussa.
Voimme nyt viimeistellä suunnan vasen ⇒ oikea todistuksen. Palauta mieleesi, mitä kaiken kaikkiaan olemme todistamassa, laittamalla symbolien vasen ja oikea paikalle oikeat väitteet. VastausLukujonossa on satapari ⇒ päistä keskelle -algoritmi löytää sataparin.
Missä kohdissa algoritmi voi lopettaa? VastausKohdassa 2 ”Jos etusormet ovat samassa kohdassa” sekä kohdassa 3.3 ”Jos se on tasan 100”.
Miksi päättelyaskel pätee ensimmäisessä lopetuskohdassa?
VastausKun etusormet ovat samassa
kohdassa, niin yhtä vaille kaikki luvut ovat vasemman etusormen vasemmalla
puolella tai oikean etusormen oikealla puolella.
Invariantin mukaan ne eivät voi olla sataparin osapuolia.
Siksi on vain yksi luku, joka voi olla sataparin osapuoli (nimittäin
etusormien kohdalla oleva luku).
Satapariin tarvitaan kuitenkin kaksi lukua, joten satapareja ei ole.
Symbolin ⇒ vasen puoli ei siis päde (lukujonossa ei siis ole
sataparia), joten oikeankaan puolen ei tarvitse päteä (algoritmin ei tarvitse
löytää sataparia).
Vastaesimerkkien avulla ilmaistuna: ei ole olemassa tilannetta jossa vasen
puoli pätee, joten ei voi olla olemassa tilannetta jossa vasen puoli pätee ja
oikea puoli ei päde.
Miksi päättelyaskel pätee jälkimmäisessä lopetuskohdassa? VastausAlgoritmi on löytänyt sataparin, joten symbolin ⇒ oikea puoli pätee. Kun implikaation oikea puoli pätee, ei ole väliä päteekö vasen puoli. Vastaesimerkkien avulla ilmaistuna: ei ole olemassa tilannetta jossa oikea puoli ei päde, joten ei voi olla olemassa tilannetta jossa vasen puoli pätee ja oikea puoli ei päde.
Olemme nyt saaneet valmiiksi suunnan vasen ⇒ oikea todistuksen. Koska vastakkainen suunta ⇐ todistettiin jo aikaisemmin, on koko todistus vasen ⇔ oikea valmis.
Tässä tapauksessa toinen suunta oli paljon helpompi kuin toinen suunta, ja eri suuntien todistamisessa käytettiin aivan erilaisia päättelyitä. Se on varsin tavallista matematiikassa ja tietojenkäsittelytieteessä.
Olemme tehneet paljon työtä ymmärtääksemme, mistä matemaattisessa päättelyssä on kyse, ja hieman myös miten sitä voi käyttää ohjelmoinnin apuna. Eiköhän nyt ole hyvin ansaitun tauon paikka! Lopuksi vielä muutama vastaesimerkki:

Kuvan lähde: kallerna,
CC BY-SA 3.0, via Wikimedia
Commons