Critical temperature in a NSN structure (MPI-parallelized)¶
Consider a NSN structure:
where the wire (of length 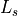 ) between the N-terminals is
superconducting. Because of the normal terminals, the critical
temperature of the superconducting wire is less than the bulk
) between the N-terminals is
superconducting. Because of the normal terminals, the critical
temperature of the superconducting wire is less than the bulk
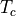 . One can easily show that the critical temperature here
is given as a solution of
. One can easily show that the critical temperature here
is given as a solution of
(1)¶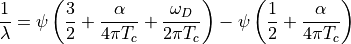
where 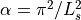 is the smallest eigenvalue of
is the smallest eigenvalue of
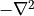 ,
, 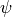 is the digamma function,
is the digamma function,
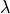 the superconducting coupling constant, and
the superconducting coupling constant, and
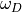 the cutoff frequency. Keeping
the cutoff frequency. Keeping 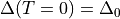 constant, (1) approaches
constant, (1) approaches
(2)¶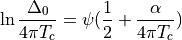
when 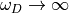 . For
. For 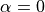 , the usual
BCS result
, the usual
BCS result 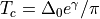 is retrieved.
is retrieved.
We can also compute this temperature numerically, by making use of the
self-consistent iteration implemented in functions
self_consistent_matsubara_iteration() or
self_consistent_realtime_iteration(). The code for this
computation is given in example-nsn-tc.py
A multicore version (without MPI) of the same script is in example-nsn-tc-multiprocessing.py
This code also serves as an example on how to write MPI-parallelized
code with the mpi4py Python module. usadel1 does not itself
support parallel computation, but sweeps over parameter ranges can be
distributed to multiple processors. To run this on 8 processors in
parallel, you can do:
mpirun -np 8 python example-nsn-tc.py
The mpi4py module exposes a standard MPI interface — if you are familiar with how MPI parallel codes work in general, you should have no problems understanding what is going on. If you want to learn more about MPI, many guides exist — for example “Rinnakkaisohjelmointi MPI:llä” by CSC Finland (in Finnish), or the book “Parallel Programming with MPI” by P.S. Pachero.
The result is shown in the figure below:
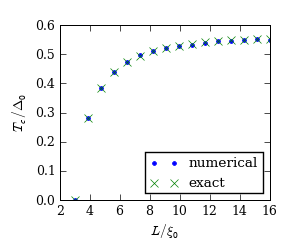
The wire is superconducting only for 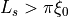 .
.

