In this section we shall investigate requirements for metamodeling languages using an inductive method. In the inductive analysis (Patton 1990) the underlying patterns, categories and rules of modeling techniques are used to identify and generalize metamodeling requirements. In our case the identification of method knowledge was based on an examination of 17 ISD methods.

Although we could examine general requirements for (meta)modeling, like simplicity and ease of reading (cf. Brinkkemper 1990, Venable 1993), our emphasis is on constructs which increase the modeling power of meta-data models: what constructs are needed to extend available semantic data models to capture and represent method knowledge. Our focus is on providing explicit constraints which deal with a combination of mechanisms provided by the data modeling language (Brodie 1984). Because our focus is on semantic data models, and mostly on ER extensions, the inherent constraints are the basic properties of the semantic data model. For example, there is a distinction between entities and relationships.

Table 4-2 summarizes the proposed metamodeling constructs derived from our inductive analysis. In the following each construct is described in more detail: in section 4.4.1 we describe constructs essential for modeling single techniques, and in section 4.4.2 constructs related to modeling multiple interconnected techniques and complete methods. When describing each metamodeling construct, we show examples of method knowledge that indicate the need for that construct. The examples of method knowledge are based on the methods summarized in Table 4-1.

In addition to the metamodeling constructs, modeling methods requires specifications of the checking mode and recognition of the different scopes for the constraints. These are described in more detail below.

TABLE 4-2 Essential constructs of a metamodeling language.

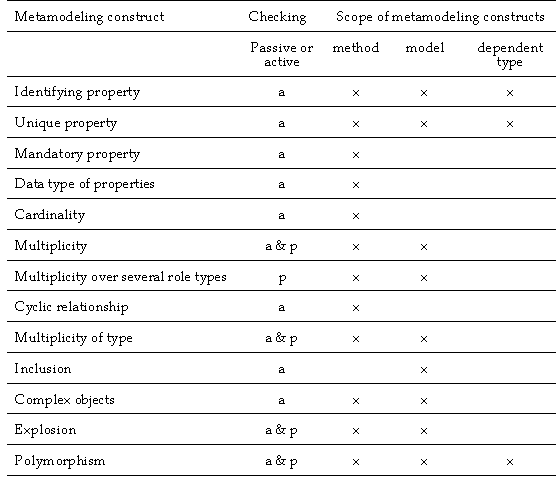
By checking mode we mean the strategy to guarantee that the rules of the method defined are followed. The checking is performed on the instance level data either actively or passively. In active checking the rules of a method are mandatory and must be satisfied at all times. In practice actively checked rules are verified each time rule-related instances are created, changed, or removed. An example of active checking is the identifier of a process in a data flow diagram. Because processes must always have identifying numbers, the construct of a metamodeling language describing an identity must be an active constraint. Passive checking, on the other hand, refers to rules of a method which are not mandatory, and are only checked at the modeler’s request. Typically, passive constraints are applicable only for completed models. Table 4-2 summarizes which checking types are useful with the proposed metamodeling constructs. In addition to supporting computer-aided checking, a passive constraint type is needed to model methods which allow the modeler to specify incomplete or conflicting models, or when active checking is not possible in practice, e.g. because of the heavy demands on computational resources if the rule was checked. Typical examples of method rules which are passively checked are instructions and recommendations, such as the number of activities in ISAC graphs (Lundeberg et al. 1982), or that each data class in BSP should have only one relationship which creates it. In practice, a data class in BSP may be created by several processes. Hence, to allow the latter situation the ‘data usage’ relationship type in the metamodel should be specified as being passively checked (IBM 1984). Instead of rigidly enforcing consistency rules, passive constraints can provide some advantages by providing information about possibly conflicting data (Nuseibah et al. 1993).

The scope of method knowledge denotes the instance space in which the rules of the method are relevant. In contrast with what is assumed in most metamodeling languages, not all rules of method knowledge can be specified within a single scope. For example, the uniqueness of a class name and a state name have different scopes (see also the example metamodels in Section 3.3.3): the former is usually unique among all classes defined in all models, even among different techniques (e.g. Henderson-Sellers and Edwards 1994), but the latter need only be unique within a single state model (cf. Embley et al. 1992), or in the context of the dependent class (cf. Booch et al. 1997). The need for different scopes of capturing method knowledge is also recognized by other metamodelers (Hochstettler 1986, Hofstede 1993, Süttenbach and Ebert 1997). Among the methods analyzed we identified three different kind of scopes for metamodeling constructs: a method, a model and a dependent type. Accordingly, a metamodeling language should recognize these scopes. In the following, each scope is described in more detail using uniqueness of properties as an example.

1) A method is the largest scope used. It refers to rules that are relevant in all instances of a method used in an ISD project. For example, in many object-oriented methods the name of a class must be unique within all the models made (e.g. Booch 1991): Two classes with the same name can not refer to different classes. Also, if two or more models (e.g. an object model and an inheritance graph (Coleman et al. 1994)) describe a class which has the same name they must denote the same class, even if some of their property types, or the relationships that they participate in are different. As a result, in a metamodel a ‘name’ of a ‘class’ must be specified uniquely within the scope of a whole method.

2) A model refers to rules that are enforced for all instances within the scope of a single model (based on one technique, or schema types (as in Hofstede 1993). For example, inside a single state transition diagram the names of states must be unique, but other diagrams can have states with the same name which, however, refer to different states. Thus, a uniqueness constraint within the scope of a whole method would be too restrictive and would not describe the method knowledge adequately.

3) A dependent type is the smallest scope which focuses on constraints that are relevant for instances that are dependent on the existence of other instances (i.e. masters). An example of a dependent uniqueness rule can be found from an entity relationship diagram in which an entity can not have two different attributes with the same name. However, attributes with the same name denoting different instances are allowed within the scope of a model and a method. For example, another entity can have an attribute with the same name, but denoting still to a different attribute. Thus, naming of attributes is dependent on the master element (i.e. in our example of an instance of the entity).

The scopes are embedded within each other, and therefore a more general scope includes limited scopes: if a scope is defined for the whole method it includes also scopes for a model and for a dependent type. For example, a constraint for unique class names within the method scope prevents also the use of the same class names inside a model. Any scope, however, does not exclude the possibility of defining other scopes for the same metamodeling construct. Consider a multiplicity construct as an example. At the scope of a model a data store does not need to participate in instances of both ‘receive’ and ‘send’ role types of the ‘data flow’ relationship type, but in the scope of a whole method, each ‘data store’ must participate in instances of both role types. This means that among IS models an instance of the ‘data store’ object type must have both updating and reading data flows but in a single diagram at least one data flow must be connected to the data store (i.e. unconnected data stores should not be included). Hence, the multiplicity rule can be defined separately for each scope. The use of method scopes are summarized in Table 4-2, and discussed in more detail in the following subsections.

In this section we shall describe the metamodeling constructs that were needed to model the 72 individual techniques selected (cf. Table 4-1). The first four constructs will focus on specifying characteristics of property types, and the next four on connections between object types. Finally, the last construct address the multiplicity of types.

Once types of a method have been introduced, their instances must be identified by using an identifier inside the scope. For example, in a class diagram a ‘class’ has a ‘name’ (e.g. Rumbaugh et al. 1991), in a data flow diagram a ‘process’ has a ‘process ID’, and in BSP (IBM 1984) an ‘entity’ has an ‘entity name’ as an identifying property. The identity of instances is typically based on an identifying property. Relationship type instances can be identified based on the participation with object type instances and/or its properties. In the former case, relationships do not have identifying properties, or in many cases they have no properties at all. An example of the latter case is message passing diagrams (e.g. Coleman et al. 1994) in which messages are distinguished by a number specifying timing and the sequence of message passing because several messages can be exchanged between the same object type instances.

Because some object types, like ‘start’ and ‘end’ states (e.g. in Booch 1991, Booch et al. 1996) do not have properties they must be identified based on the context (e.g. a start state of a given state transition model), or have an internal identifier. The former means that the context forms another part of the identifier. The latter one is typically used in CASE tools. Text-book methods, however, do not recognize internal identifiers because of their ‘pen and paper’ -mentality.

In the methods analyzed all three types of scope were used. First, in most object-oriented methods (e.g. Rumbaugh et al. 1991, Coad and Yourdon 1991a) the ‘name’ of a ‘class’ and the ‘number’ of a ‘process’ form identifiers inside all models of a project (i.e. method scope). Second, the ‘name’ of a ‘state’ identifies states inside a single state transition diagram, but not within a whole method, since two or more state transition diagrams can have states with the same name (referring to different states). Third, an identifier can be dependent on other instances. For example, in UML (Booch and Rumbaugh 1995) classes can have a scope according to the enclosing category: the identity of a ‘class’ object type is dependent on the ‘category’ object type it belongs to. Similarly, in ISAC (Lundeberg et al. 1981) the code of an elementary information set recognizes the instances only as a subset of a non-elementary information set. Therefore, the master (i.e. a category in the former and a non-elementary information set in the latter example) also has an identifier, and it forms part of the identifier for instances of dependent type.

The identity constraint can be characterized as an active constraint since in modeling tools they can be analyzed each time an instance of the property type (i.e. value) is created, changed, or deleted. Active checking, however, can lead to time consuming computation and usually CASE tools can not analyze identifiers actively. For example, active checking at the level of the whole method necessitates that all models and their instances are inspected.

A unique property constraint specifies that an instance of a property type has a unique value inside the enclosing scope. The unique constraint prevents the homonym problems which almost every method warns against: the use of the same value for different instances of a property type. Typically an identifier must be unique, but also other properties may need to have unique values.

Among the methods analyzed a unique constraint is needed in all method scopes. A unique property based on the dependent type can be found from class diagrams (e.g. Rumbaugh et al. 1991) in which a class can have only one attribute with the same name. Similarly, in the ER model (Chen 1976) a name of an attribute must be unique among the attributes connected to an entity. A unique property constraint within a model is relevant for example in data flow and state transition diagrams in which names of processes and states must be unique inside the diagram. Among relationship types a unique property for a message passing sequence (Coad and Yourdon 1991a, Coleman et al. 1994) is relevant inside a single model. In the method scope the identifying number should be unique among all instances of a ‘process’ object type.

In addition to different scopes, a metamodeling language should be able to specify uniqueness of the same property types for several object types. For example, in Coad and Yourdon (1991a) both abstract classes (i.e. a ‘class’) and classes with instances (i.e. a ‘class-&-object’) must share the same property type. Similarly in Booch (1991) a ‘metaclass’ and an ordinary ‘class’ can not have the same value for class names (i.e. class name values are unique among both types).

A uniqueness constraint can be considered as being passively checked at least in the scope of a method, since all values of a given property type are not necessarily available and thus can not be checked instantly. In contrast, a model and a dependent type have a limited number of instances and thus can be checked actively.

Some methods include rules which state that properties must have values at all times (i.e. null values are not accepted). Accordingly, a metamodeling language must distinguish mandatory and optional instances for property types. Generally, properties are optional, but identifying properties are mandatory. For example, a ‘number’ as an identifier and the ‘name’ of a ‘process’ object type in a data flow diagram are mandatory, but in UML (Booch and Rumbaugh 1995) the ‘name’ of a ‘state’ is optional. To ensure that data dictionaries can be formed parallel to modeling (as proposed in Yourdon 1989a), a documentation property type used in the metamodel of SA/SD for creating a dictionary must be defined as mandatory.

The mandatory constraint is not restricted to any specific scope, such as being dependent on instances of other types, or used in a model. Thus, we expect that the only scope for mandatory instances of property types is the whole method. Furthermore, this constraint can be checked actively in a computer-aided environment each time the property value is changed, or a new instance of a property type is created. In practice a need for passive checking would most likely arise because all properties are not necessarily known while creating models, leading to undefined property values.

Design information captured in properties of other types are specified with various data types. From a metamodeling point of view, data types are needed to restrict the possible values of properties. Recent methods, such as most of the object-oriented ones, tend to have complex data types. One explanation for this is CASE tool support, which on the one hand demands data type definitions to implement the tool support, and on the other hand offers mechanisms to manage larger models and more complex data types.

Among the most typical data types are integer, string, text, and Boolean. A number is commonly used as identifying property or for describing the order among relationships (e.g. Coleman et al. 1994, Coad and Yourdon 1991a). A string is used for short descriptions; a text for a larger body of specifications such as definition in a data dictionary or pseudo code (Yourdon 1989a). Boolean describes single-value “on-off” or “true-false” characteristics such as the persistence of a class (Henderson-Sellers and Edwards 1994). In addition to plain data types, some methods, such as ISAC (Lundeberg et al. 1981) and BON (Walden and Nerson 1995) include more detailed specifications for the internal structure of each data type. For example, in ISAC, only one-digit numbers can be used for identification of activities, and in UML (Booch and Rumbaugh 1995) the possible values for visibility are limited to three (i.e. public, private, protected) and access of attributes into four (i.e. writeread, write, read and none). Some methods have more complicated rules for the textual description: in IDEF (FIPS 1993a, p 11) arrow labels can not consist of reserved words, and in ISAC the numbers of information sets also include the number of the activity creating the set. In BON (Walden and Nerson 1995) the structure of textual properties is the most extreme: there is a whole language for defining instance-related assertions through properties related to other instances. Thus, a metamodeling language should provide, together with the method-related data types, the possibility to specify the syntax of data types, and for checking the syntax. This requirement, however, goes beyond the typical use of data modeling languages as discussed in Section 4.5.3.

In addition to the property types which can be understood of having one value only as above, a metamodeling language must also identify collections. Collections are mostly used in object-oriented methods. For example, a class can have multiple attributes and operations.

Property type definitions can also be extended by defining default values and predefined values. These mean that a metamodel defines some instance values for property types. A default value defines a single instance for a property type to be applied if nothing is added. Thus, it is usually applied with property types defined as mandatory. Predefined values are typical in the cardinality constraints used in data models because they apply different naming policy for cardinality values. Some expect symbols instead of numbers: some describe cardinality with number only (typically a maximum value), whereas others describe cardinality as a pair of values (i.e. minimum and maximum). Checking a data type can be done actively. Because data types do not focus specifically to any scope of the constraint, the method scope as most general seems to be most applicable.

A cardinality constraint defines a minimum and a maximum number of instances of a role type a relationship type instance can have. A role construct, used either explicitly or implicitly in all major semantic data models, defines the part played by an object in a relationship, such as in NIAM, (Nijssen and Halpin 1989, ter Hofstede 1993), OPRR (Welke 1988, Smolander 1991), or CoCoA (Venable 1993). The minimum number is typically 1 in the roles of binary relationships, since a relationship can not normally exist independently without connected objects. For example, a ‘message passing’ relationship in an object diagram (Coad and Yourdon 1991a) must have both ‘send’ and ‘receive’ roles. It is also possible, however, to define the minimum constraint as zero to denote relationships that do not need to have other role(s). For example, the object interaction graphs of Fusion (Coleman et al. 1994) allow one to define message passing between objects in which the sender outside the model boundary is not specified. More typical situations of zero minimum cardinality are cases in which a relationship can be extended with an optional role type, e.g. with an associative object type (Yourdon 1989a) in entity relationship diagram, or with a creation of an object in data flow diagrams (Rumbaugh et al. 1991). Hence, the minimum constraint for the optional role type is normally zero and for a mandatory role at least one. Consequently, the deletion of mandatory roles (minimum cardinality one) removes also the whole relationship and related instances of role types. Moreover, if ternary relationships have their own modeling constructs, as in the class diagram of UML (Booch and Rumbaugh 1995) the minimum role cardinality is 3: Each relationship must have at least three instances of a role type. Otherwise the relationship is a binary one and should be defined with a different relationship type.

Within the methods analyzed the maximum cardinality of a role is either one (1) or many (M). The maximum cardinality is one in binary relationships with two role types, e.g. in the relationships of a structure chart, a module diagram (Yourdon 1989a) and a platform diagram (Booch 1991). Thus, if an instance of a ‘call’ relationship type exists in a structure chart it can not have more than one instance each of ‘send’ and ‘receive’ role types. The maximum cardinality of a role type is many in n-ary (sometimes also called branching) relationships. For example, an ‘inheritance’ relationship (also called generalization, gen-spec, supertype) in object-oriented methods can have only one (1,1) ‘superclass’ role but one to many (1,M) ‘subclass’ roles.

None of the methods modeled include restrictions on the cardinality rule within different scopes. Since they implicitly expect that the same instance of a relationship can exist only among the same role type instances, the most relevant scope is a method. This allows us also to support methods which use the same relationship type instances in several techniques (e.g. an inheritance in Henderson-Sellers and Edwards (1994)). Moreover, checking of both minimum and maximum constraints for the role cardinality are active: They can be checked each time a relationship is created, an existing role is deleted, or a new one added.

A multiplicity constraint is needed to define a minimum and a maximum number of role instances an object instance may have. With the minimum value we can define that an object instance must be connected to at least a specific number of instances of this role type, and with the maximum value that an object type instance can not be connected to more than a specific number of instances of this role type. The need for the minimum constraint can be found from modeling a state diagram (e.g. Booch 1991) in which a ‘start state’ must be connected to at least one ‘send’ role of a ‘transition’ relationship, and from techniques that are based on tree structures, such as JSD (Cameron 1989). An example of the maximum constraint is inheritance found from most class diagrams allowing only single inheritance (e.g. Rumbaugh et al. 1991): a class can only participate once in a subclass role.

Typically, a multiplicity constraint for a role is zero-to-many (0,M): an object type does not need to be connected to an instance of a specific role type, but it can be connected to many instances of that role type. Other common values found for minimum multiplicity are one for mandatory roles, and two for object types which must occur at least twice in a specific relationship (e.g. a ‘condition’ object must participate in at least two ‘connector’ relationships (Coad and Yourdon 1991a). Hence, the multiplicity value for a ‘condition connector’ role type should be two-to-many (2,M).

Methods use multiplicity constraints within the scope of a model or a method. An example of the former is a ‘start state’ in a state transition diagram: each start state must be connected to one state and thus the minimum multiplicity constraint must be checked for each instance of a start state. A typical example of the latter scope can be found from data flow diagrams in which an instance of a ‘data store’ must participate in instances of ‘send’ and ‘receive’ role types of a ‘data flow’ relationship type, but not necessarily in one diagram (Yourdon 1989a, p 282). Similarly among all collaboration diagrams (Booch and Rumbaugh 1995) each instance of an ‘object’ must send and receive at least one message, but not necessarily inside the same model.
A maximum constraint can be checked actively, but the minimum constraint is passive: it can not be satisfied during model building, unless it is zero, because objects can exist while they are not related to other objects (i.e. connected to a role type instance).

In addition to the multiplicity constraint, modeling of method knowledge requires constraints between different role types. Basically, this constraint is needed to prevent instances of object types that are not participating in any relationships. In other words, this constraint supports a rule stating that an object type instance must participate in at least one of the specified roles. In NIAM (Hofstede et al. 1993) this constraint is called a total role constraint. Examples of method knowledge necessitating the multiplicity constraint over several role types are those of ISAC and SA/SD within the scope of a model. An ‘information set’ instance must participate either in a ‘predecessor’ instance, or a ‘successor’ instance (Lundeberg et al. 1981), and a ‘data store’ instance must participate at least once in a ‘send’ or a ‘receive’ of a ‘data flow’ (Yourdon 1989a). The multiplicity rules identified among the methods analyzed do not require more complex multiplicity constraints, such as mandatory participation among two or more of the specified roles, or maximum multiplicity over several roles. Together with the cyclic relationship constraint, modeling techniques using tree structures, such as JSP (Cameron 1989), can be specified: one of the modules must be the root of the tree.

All these constraints are originally specified to be applicable inside a single diagram only, i.e. in the scope of a model only. Although the methods modeled do not apply this constraint within other scopes, it could be applied for the scope of the whole method as well (e.g. no more than 10 flows to an external).

Although the metamodeling construct could be checked actively when an object is created or a relationship deleted, passive checking is more suitable. The reason for this is simple: all objects and relationships to be checked are not necessarily available and models would too often encounter this rule leading to heavy model checking.

A cyclic relationship involves connections between instances of object types via instances of a single relationship type, thus forming a cycle. Basically, in the methods analyzed two types of cyclic relationships exist: a direct one, in which the same instance of an object type can participate in both ends of the same relationship type instance, and an indirect one, in which the cycle can be formed via one or several additional instances of object types (with associated relationship type instances). It must be noted that the indirect cyclic relationship necessitates two or more instances of a relationship type. Table 4-3 illustrates examples of different cyclic relationships found in the methods modeled. Accordingly, a metamodeling language should distinguish both of these cyclic relationships types and allow method engineer to allow or prohibit them.

TABLE 4-3 Examples of cyclic relationships in the methods modeled.

An example of a direct cyclic relationship can be found in state transition models (e.g. Rumbaugh et al. 1991, Booch 1994) which allow a transition from a state to itself, and in the object interaction graph of Fusion (Coleman et al. 1994) in which an object can send a message to itself. In other techniques, direct cyclic relationships are prohibited: in a message trace diagram (Booch and Rumbaugh 1995) an object can not send a message to itself, in a structure chart a module can not call itself (Yourdon 1989a), and in all object-oriented methods a class can not inherit itself. Inheritance serves also as an example of a prohibited indirect cyclic relationship. Similarly, indirect cyclic relationships are not possible in tree structures, as in JSD (Jackson 1976). Data flows in data flow diagrams, transitions in state transition models, and message passing in object diagrams (Coad and Yourdon 1991a) can form indirect cyclic structures. None of the methods analyzed, however, restricts the “length” of an indirect cyclic relationship structure, nor presents any specific scope for this type of constraint. Because the dimensions above are not totally orthogonal, only three basic patterns of cyclic relationships were found: those allowing both types (e.g. state models), those allowing indirect relationships only (e.g. A-graph), and those forbidding both types (e.g. tree structures like JSD). Thus, cyclic relationships which allow direct cyclic relationships but not indirect ones were not found from the methods.

Metamodeling constructs for cyclic relationships were not dependent on instances of the same or other relationship types. For example, a data flow from a process to itself can occur even if the same process receives a control flow (Ward and Mellor 1985), i.e. has instances of other role types.

The checking of both cyclic relationships types can be carried out actively although in most CASE tools the checking of the indirect type is passive because of its high computing requirements. Here, all relationships and objects participating in these relationships should be available. The scope of the constraint is all models since none of the methods included any more specific scope.

A multiplicity construct for types is needed to define how many times instances of the same type must or can exist inside the enclosing scope. For example, ISAC (Lundeberg et al. 1981) has rules which specify that a maximum of 9 instances of a given type (‘activity’ or ‘information set’) should exist inside a single graph. In IDEF (FIPS 1993a) the possible number of functions in a model should not exceed 6, and also BSP (IBM 1984) recommends the number of data classes or business processes in an IS architecture plan. The multiplicity constraint is relevant for both object and relationship types. In most methods, the multiplicity constraint for object types is one-to-many (1,M): They must have one to many instances. However, the multiplicity of the ‘start’ state in most state transition models is zero-to-one (0,1): start states are optional and only one start state can exist in a model. Whereas object types can have different minimum and maximum values for multiplicity, relationship types are restricted only to a possible mandatory existence (i.e. with a minimum value). For example, at least one instance of a ‘data flow’ must exist in a data flow diagram and one instance of a ‘transition’ in a state transition diagram, but an ‘inheritance’ does not need to have instances in a class diagram. None of the methods analyzed include rules which set a maximum number for the occurrence of instances of relationship types.

Multiplicity of types should not be confused with multiplicity of the same instance: how many times the same instance, e.g. a process named Verify Orders, exists in a model. A metamodeling construct for instance multiplicity seems to be unnecessary since none of the methods includes such restrictions. Typically, to simplify crossing relationship lines in a model an instance can be replicated and all copies have the same properties. For example, in SA/SD (Yourdon 1989a) the same instance of the ‘store’ object type can be drawn to many places in the data flow diagram. The same relationship instances can also occur, as in OSA (Embley et al. 1992): an interaction relationship can occur both in the object-behavior model and in the object-interaction graph and it has the same properties for both instances (e.g. a trigger and an action). However, it must be noted that the same relationship type with the same instance information can not occur in any method more than once between the same object type instances (i.e. no duplicate relationships are allowed). This constraint is an inherent constraint (cf. Brodie 1984). As a result, it is not necessary to specify this constraint with an additional construct of a metamodeling language.

In the methods analyzed the multiplicity constraint is applicable at the level of a single model (e.g. ISAC), and of a whole method (e.g. BSP). Furthermore, although the multiplicity can be checked actively each time a new instance of a type is added, it should not be restrictive: it should be possible to create models that violate the multiplicity rule during modeling. Checking minimum values actively would also be inappropriate, since new models would violate the constraint.

In this section we describe those metamodeling constructs essential to model interconnected techniques. Although the proposed constructs are mainly a prerequisite for modeling a whole method, some of the required constructs are useful for modeling single techniques.

The first requirement in specifying a whole method is the allocation of types into techniques. For this purpose, a metamodeling language must include a construct called inclusion (according to Tolvanen et al. 1993). The inclusion can be defined as an aggregation which can exist only between a technique and its types. For example, at the technique level the ER model includes entity, relationship and attribute types. At the type level, the GOPRR definition allows us to describe the graph type ‘ER model’ and its components. The type level cardinality for inclusion is many to many, since types can belong to many techniques and a technique usually consist of multiple types. For example, in the GOPRR metamodel of BSP the ‘business process’ belongs to three different techniques (cf. Section 4.3.1).

In addition to object types, relationship types and role types can belong to multiple techniques. For example, an ‘interaction’ in OSA (Embley et al. 1992) can belong both to interaction models and state models, and an ‘inheritance’ in MOSES (Henderson-Sellers and Edwards 1994) can be part of class and inheritance diagrams. Because of the similarities in the type level method definitions, these methods also explicitly allow the occurrence of the same instances in different techniques. For example, the same instance of an ‘interaction’ defined in an object-interaction model describing message passing between a set of objects can also be used to define an external trigger in an object-behavior diagram describing possible states of a single object (cf. Embley et al. 1992).

The checking of inclusion can be regarded as active since this constraint is already specified in the metamodel and does not necessitate an instance based evaluation: each time an instance is created or an existing instance is added to a model it must satisfy the type level definition. Because of the focus on specifying a type of a technique, the inclusion constraint is relevant only within the scope of a model.

The majority of the methods modeled, especially the object-oriented ones, apply complex objects. By a complex object we mean an abstraction mechanism which allows us to build aggregate-component structures among the types of the method. The aggregate object suppresses details of the underlying relationship between components (Smith and Smith 1977). Complex objects are also distinguished from aggregation of attributes used to define attributes of entities (Alegic 1988). In line with Iivari (1992) we make a distinction between the concept of a relationship and a complex object. The former is used for example in most dialects of ER-based data modeling languages. In fact, the ER model proposed by Chen (1976) only included relationships. Because our interest is on the type level definitions of methods it must be noted that instance level aggregation structures, such as aggregation (in Rumbaugh et al. 1991) and whole-part (in Coad and Yourdon 1991a), can be described with relationships in the metamodel. Complex objects are used as modeling constructs in specifying functional decomposition (cf. Yourdon 1989a), aggregation (cf. Coleman et al. 1994), concurrency (cf. Booch and Rumbaugh 1995), and clustering (Walden and Nerson 1995). Hence, our focus here is on those structures that are not described with relationship types and necessitate the use of complex objects. Several studies on metamodeling (e.g. Smolander 1991, Venable 1993, Saeki and Wenyin 1994) reveal limited support for modeling complex objects (sometimes also called hierarchical structures) with data model based metamodeling languages.

Iivari (1992) reviews complex objects as a conceptual abstraction mechanism and classifies them into five dimensions. These are: 1) dependent/independent, 2) connected/unconnected, 3) mandatory/optional, 4) exclusive/shared and 5) recursive/non-recursive. In the following we describe the categories in more detail and apply them at the metalevel to recognize the different kinds of complex objects used in methods. Based on the analysis we found 11 different kind of complex objects summarized in Table 4-4. The five first rows of the table correspond to the various structures of complex objects proposed by Iivari (1992).

1) The dependent/independent dimension defines whether a component object can exist independently of the aggregate object. If a method employs dependent components it leads to a top-down process of model building, since it is not possible to create components without an available aggregate object. Similarly, in a dependency situation, deleting an aggregate object will delete all of its components in that scope. An example of a dependent complex object is a functional decomposition in a data flow diagram (Yourdon 1989a). Here a process can be divided into a new subdiagram describing its subprocesses. Another example is a composite (Booch and Rumbaugh 1995) in which a class must exist before its component objects (i.e. instances of a class) can be defined. Functional decomposition is also applied in other methods, e.g. ISAC for defining activities with A-graphs (Lundeberg et al. 1981), in IDEF for decomposition of functions (FIPS 1993a), and in other techniques that employ data flow diagrams (e.g. Rumbaugh et al. 1991, Shlaer and Mellor 1992). Here we handle all these as examples of functional decomposition. An example of an independent complex object is a clustering (Walden and Nerson 1995): a cluster symbol (with an attached name) can be drawn around a set of classes to specify that they belong to the same group. Because empty clusters are meaningless, one or more component classes must exist. None of the methods analyzed, however, includes a multiplicity rule which specifies the required number of instance components. The construct for defining dependent components can be checked actively each time a dependent component is created or an aggregate deleted.

2) Connected/unconnected defines whether the internal relationships between the components of a complex object can be omitted. This dimension is not valid for metamodeling, since connected components are always possible: None of the methods offers rules which state that the internal relationships can not be specified together with the aggregate object.

3) Mandatory/optional describes whether a complex object can or cannot exist without any specified component. ‘Mandatory’ necessitate the existence of components and a bottom-up modeling approach. Typically, methods which propose their own object type(s) as an aggregate object expect that components exist before the aggregate object is specified. For example, a boundary in an object model (Coleman et al. 1994) should not be specified without the existence of its components (i.e. an empty boundary is not possible). Similarly, empty categories in UML (Booch and Rumbaugh 1995) are meaningless. In contrast, methods applying the same type both as an aggregate and a component often propose a top-down refinement, although a bottom-up approach is also possible. For example, in a data flow diagram, a process can exist even though it is not decomposed into a subdiagram. A mandatory rule can be checked each time an aggregate object is created or its component deleted.

4) The components of an aggregate can either be exclusive or shared. Techniques which form hierarchies, like composite (Booch and Rumbaugh 1995), functional decomposition (Yourdon 1989a) or clusters (Walden and Nerson 1995) presuppose that a component can not directly belong to more than one aggregate object. In contrast, a boundary (cf. Coleman et al. 1994) allows that a class (a component) can belong to many functional systems shown through boundaries (an aggregate). Similarly, aggregation structures in object-oriented methods specified with a complex object (e.g. Coleman et al. 1994) instead of a relationship type (as in OMT, Rumbaugh et al. 1991) allow shared component classes. The notation used here for an aggregation as a complex object, however, easily leads to complex representations once components are shared due to overlapping aggregate representations. Moreover, components that are defined to be exclusive must be checked during modeling: the same instance of a component type can not belong to another complex object.

5) Recursive/non-recursive complex objects. This final dimension in Iivari’s classification defines whether or not the component objects can be of the same type as the aggregate object. An example of a recursive complex object is a subject (Coad and Yourdon 1991a) which can contain classes or other subjects. None of the methods modeled had rules which required non-recursive structures.

TABLE 4-4 Structures of complex objects in methods.

The five structures applied here reveal some similarities and differences in the use of complex objects as a modeling construct in ISD methods. There are, however, additional differences between the structure and behavior of complex objects that are not yet addressed. For example, the structure of a composite is not similar to a decomposition used in data flow diagrams, nor is a subsystem (cf. Henderson-Sellers and Edwards 1994) similar to a subject (cf. Coad and Yourdon 1991a). To identify these differences two additional dimensions are required, namely independent/dependent relationships of the aggregate object and aggregated/non-aggregated relationships. Both of these dimensions are included in Table 4-4 as the last two rows.

6) The independent/dependent relationship of an aggregate object specifies whether an aggregate object in a complex object can participate in relationships which are independent of the relationships of its components. For example, one difference between the structure of a composite and functional decomposition is that in the composite an aggregate (i.e. class) can have relationships, such as inheritance, which are not related to its components. Naturally, the components representing instances of a class have attributes which the class may have inherited. Similarly in nested state models (Yourdon 1989a, 267, Booch and Rumbaugh 1995, p 33) a state which has substates (i.e. a composite state in UML) can participate in transitions which are not defined for any of its substates. The important difference in this dimension is that in functional decomposition a decomposed process can not have relationships other than those included in a subdiagram. This dimension also reveals other differences between relationships of complex objects. Some aggregates (i.e. boundary, subject, and process group) do not participate in any relationships by themselves but only through their components. Here a complex object is concerned with a collection of its components without any specific relationships (cf. Kim et al. 1989).

The case of dependent relationships, however, does not necessarily lead to the use of the same instances of relationship types both for a composite and for an aggregate. We did not include this difference among the dimensions of complex objects, since the difference can be specified in metamodels simply by allowing object types to participate in different relationship types. Independent relationships do not require instance-based checking, since they are already allowed on the type level. In contrast, dependent relationships of an aggregate and its components originating outside the complex object must be checked actively.

7) Aggregated/non-aggregated relationships define whether relationships of components connected outside the same complex object are collected into a new instance of the same or a different relationship type. Thus, we expect here that the relationships of components are compressed into new aggregated relationships. This dimension is valid only for those aggregates of complex objects which can participate in relationships. Examples of aggregate relationships can be found from some object models: a subsystem (MOSES, Henderson-Sellers and Edwards 1994) or a cluster (BON, Walden and Nerson 1995) has its own relationships “collecting” the relationships among the components of different subsystems or clusters. In MOSES these aggregate relationships are called a collaboration and in BON a compression of client relationships. The aggregated relationships can be of the same or a different type from the components’ relationships. In the former case an object group (cf. Walden and Nerson 1995) can not sent or receive messages that are independent of the messages being send or received by its components. An example of the latter case is a category dependency describing only client-supplier relationships of the categories. These dependencies are, however, based on underlying relationships between classes of different categories. Methods which do not allow aggregated relationships either apply exactly the same instances of relationships for the components, such as in functional decomposition, or allow relationships for the aggregate which are independent of the relationships of its components (as discussed in the sixth dimension). An aggregation of relationships requires that each time a first relationship is created or the last one deleted the same operation should be executed for the aggregated relationship as well. This demands active checking of aggregation rules.

If we assume that all these dimensions are orthogonal, we can obtain 128 basic alternatives for complex objects. All possible alternatives identified in Table 4-4 are not necessarily, however, relevant for metamodeling of complex objects. The analysis of complex objects shows that some complex objects follow a similar structure. A subject (Coad and Yourdon 1991a) and a boundary (Coleman et al. 1994), nested states and a composite (Booch and Rumbaugh 1995), and an object group (Walden and Nerson 1995) and a subsystem (Henderson-Sellers and Edwards 1994) belong to the same categories in Table 4-4. These similarities limit the number of different structures found among the methods into 8. As a consequence, the metamodeling language must support the modeling of each conceptual structure of complex objects to capture method knowledge. In the 17 methods selected we found 11 complex object types. It must be noted that other alternative types for complex objects are also possible.

In addition to the seven dimensions of complex objects, the possible scope of this construct divides methods into two categories: those treating complex objects globally within the scope of a method, and those allowing different complex objects of the same aggregate object in different models. Functional decomposition and clustering according to the system view belong to the first category. Each decomposed process or cluster has the same components even though they would be represented in different models. Composite and subjects are examples of the model scope. A class can participate in multiple composite structures, each structure describing its instances (objects) in various contexts. Similarly, the same subject can have different components in different class diagrams.

To summarize, the following aspects of complex objects need to be recognized and represented with a metamodeling language. First, since all methods allow relationships to be described between components the second dimension - connected component objects - seems useless in metamodeling. Thus, we expect that a metamodeling language will not need to distinguish complex objects based on the possibility to have relationships among the components. Iivari (1992) too has doubts about system models that do not specify internal relationships. Second, dependency and mandatory components are alternatives since complex objects can be defined either in a top-down, or in a bottom-up manner. In most situations of IS modeling both of these strategies are possible. Thus, the methods analyzed here provide either one or both of the options. Third, a metamodel should define whether the same object can or can not be a component in many complex objects. None of the methods proposes other restrictions, such as a component having to belong to a specific number of complex objects. Fourth, since non-recursive complex objects were not found, recursive structures do not need to be distinguished in the metamodeling language. Fifth, it should be possible to define complex objects in which an aggregate object can participate in relationships separately from relationships that its components have outside the complex object. Methods apply either the same relationship types for the aggregate object as its components have, like in nested state models, or new relationship types, as in dependencies of categories in UML. Finally, a metamodeling language must have constructs to distinguish relationships of components which must be aggregated to from relationships of the aggregate.

One of the most common approaches to integrate techniques is linking of a type in one technique to a set of types described in another technique. We call this metamodeling construct an explosion in the GOPRR model (Kelly et al. 1996). According to our analysis of complex objects, explosion structures are typical between different techniques, and they do not carry as much semantic information about the instance level linkages as complex objects. For example, relationships of the exploded type are meaningless as the relationships in the target model are based on another technique. According to most object-oriented methods the behavior of a class from a class diagram (see also example metamodels in Section 3.3.3) or a use case from a use case diagram can be described with state diagrams (cf. Coad and Yourdon 1991a, Booch and Rumbaugh 1995). Similarly, according to the balancing rules of SA/SD (Yourdon 1989a, p 283) each control process must be associated with a state transition diagram. Various explosion structures can be characterized according to 1) the type of the explosion source, 2) the cardinality of the explosion, 3) an exclusive or shared explosion target, and 4) active/passive checking of explosion cardinality constraints. Each of these characteristics is described below.

1) Type of the explosion source. Among the methods analyzed, three different kind of explosions could be found depending on the metatype that forms the source of the explosion. First, an object type, like a ‘data store’ or a ‘class’, can be a source for the explosion. A second possible source type is a relationship, such as a ‘transition’ which in a state model explodes into a data flow diagram (Rumbaugh et al. 1991). Third, a property type of an object or a relationship type can also be refined by explosions. For example, in Coad and Yourdon (1991a) each ‘service’ of a ‘class’ can be described in service charts.

2) Cardinality of explosion. Among the methods analyzed, several limitations to the number of explosion links are defined. These constraints can be represented by attaching cardinality constraints to explosions. Both a source type and a target technique must have a cardinality constraint and both a minimum and a maximum cardinality are needed for a complete definition. At the source part, a cardinality defines how many explosion links an instance of the source type can or must have. Typically, the minimum cardinality represents whether an explosion is mandatory, and a maximum cardinality specifies if more than one explosion link is allowed. An example of the minimum cardinality can be found from SA/SD (Yourdon 1989a) in which each data store must be described in more detail with an ER diagram, and in a data dictionary. Most object-oriented methods generate a need for a maximum cardinality: in most methods, the states of a class can be described in several state models. Therefore, the total cardinality at the source type is zero-to-many (0,M). Moreover, because in a data flow diagram a process can be specified only in one process specification the maximum cardinality is one.

At the target part, the minimum cardinality specifies whether a target model needs to be linked to one or more instances of the source type. For example, in Yourdon (1989a) no floating process specifications are allowed, and in Coad and Yourdon (1991a) service charts unconnected to a service of a class are not allowed. Especially in cases of multiple possible explosion links to the target technique, the minimum cardinality of the explosion target is zero. For example, in OMT (Rumbaugh et al. 1991) each data flow diagram does not need to be connected to an object type ‘state’ as it can be a target for an explosion of an relationship type ‘transition’ as well. Thus, the minimum cardinality for an explosion link between a ‘state’ and a ‘data flow diagram’ is zero. The maximum cardinality of the target type on the other hand specifies whether more than one instance of a source type can explode into the target model. Although in most situations only one explosion link is allowed for the same target, some methods, like FUSION (Coleman et al. 1994) or OMT (Rumbaugh et al. 1991), allow many instances of a source type to explode into the same instance model. Hence, the maximum cardinality is many. In Fusion, a model describing interaction between several objects can be a target for several explosion links from different instances of an ‘object’ specified in object models. Similarly, an UML collaboration diagram specifies messages sent between several instances of a ‘class’ described in a class diagram.

3) Exclusive explosion links restrict whether instances of two or more different source types can explode to the same target model (i.e. instance model). In SA/SD a process specification can be a target of explosion links from two types, as both a ‘process’ and a ‘control’ can have operation specifications. These specifications, however, must be defined as exclusive because a process specification can belong to only one instance. An example of a shared target model is explosion of instances of both a ‘class’ and a ‘class utility’ into the same object diagram (e.g. Booch 1991).

4) Active/passive checking. Because the cardinality as such does not describe a precedence between a source and a target this procedural aspect can be described with a checking rule: if the checking of the minimum cardinality on the target side of the explosion link is defined as active it can be used to specify top-down structures of explosion links. In the earlier example of exploding a process into process specifications, the mandatory and active checking of minimum cardinality assures that process specifications can not be specified without a related instance of a ‘process’. If a source element of a top-down explosion link is deleted, the target models should be removed as well. Active checking of the minimum cardinality on the source part, on the other hand, can be used to define a bottom-up strategy for modeling explosion structures. None of the methods analyzed, however, applied bottom-up structures. In the explosion links analyzed the maximum cardinality for both a target and a source can be checked actively.

Finally, the explosion constraint must be related to either of the two possible scopes; a method or a model. The method scope defines that the explosion constraint is relevant for all instances of the source type. Alternatively, explosions can be relevant for each instance in a model only. In the former case, explosions are defined for all instances of the type, and in the latter case, the same instance of a source type can have different explosion links in different models. An example of the method scope is an instance of a class which explodes always to the same state model regardless of the class diagram in which it is represented (i.e. a class always has the same lifecycle). An example of a model scope is when a transition in a state model explodes to a collaboration diagram specifying a scenario in which the transition occurs as a message passing (e.g. Booch et al. 1997).

Methods consisting of multiple techniques inspect systems from different views: each technique focuses on a specific view and these different views are integrated in the whole method. In addition to using the same types as a part of different techniques on the metalevel (defined with the inclusion construct) methods apply polymorphism of types to indicate instance level connections (Venable 1993). By polymorphism we denote connections between two or more instances of different types based on sharing the same values as their properties. Types can also be of a different metatype (e.g. an object which is represented as a relationship in another model). In other words, ISD methods use different types to describe the same instances. Polymorphism is applied mostly in methods which use horizontal integration for connecting instances of different models, e.g. names used for data stores in data-flow diagrams being redefined for cross-checking with an ER model.

Different structures of polymorphism can be identified based on 1) coverage over one or more techniques, 2) the number of properties shared, 3) the number of type instances related, and 4) a possible dependency among the types of a polymorphism structure. As a consequence, a metamodeling language should be capable of representing all the different structures discussed below. These different structures are collected into Table 4-5 together with examples to be discussed in more detail below.

1) Coverage. Polymorphism can exist between types included in one or several techniques. An example of the former is a qualifier of an association in some class diagrams (e.g. Rumbaugh et al. 1991, Booch et al. 1997). Qualifier is also one of the attributes of a class participating in the association, i.e. the value for the qualifier must also be defined as an attribute in the related class. As a result, it is not adequate to model a qualifier and an attribute only as property types, as they need to be related to indicate sharing of the same property values. Similarly, a discriminator of the inheritance relationship must be an attribute of the superclass. An example of the latter, polymorphism between techniques, can be found from the balancing rules of SA/SD (Yourdon 1989a, p 283). A data flow in a DFD and a call relationship in a module diagram, as well as a control flow into a control process and a condition of a transition in a state model, describe the same instance in different models. Similarly, almost all object-oriented methods apply polymorphism to describe that an action (or an operation) in a state transition model and a service (or a method) of a class describe the same instance (Coad and Yourdon 1991a, see also the metamodeling example in Section 3.3.3). To specify these structures adequately an additional supporting metamodeling construct is required.

TABLE 4-5 Examples of different kinds of polymorphism in methods.

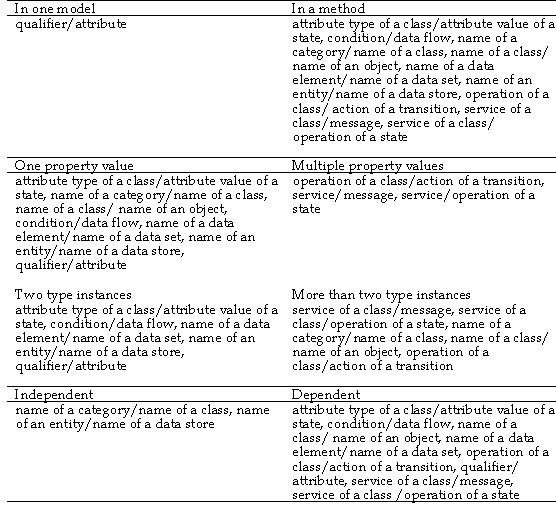
2) Number of properties shared. Polymorphism can be based on sharing more than one property value at a time. This necessitates that more than two property types are involved in the polymorphism. The qualifier example, discussed above, is based on sharing one value only between two property types: the ‘qualifier name’ and the ‘attribute name’. Object-oriented methods like MOSES (Henderson-Sellers and Edwards 1994) apply polymorphism for several instances of property types at the same time: a service of a class in a class diagram and a message in an event model have several common values, such as name, parameters, and return types. Hence, when messages are described in an event model, properties of a message must refer to a set of the properties of one service. According to the majority of method descriptions, it is not possible to have messages other than those defined as services of classes. As a result, if one of the property type instances is shared, it necessitates also that related instances of other property types are shared as well. For example, the same instance of a message type can not have different return values as properties. Similarly, in UML each object has a class name to indicate the class that the object belongs to, and therefore the attribute values of the object must refer to those defined for the class. Accordingly, a metamodeling language should also represent instance level connections between related properties.

3) Number of type instances related. Polymorphism can occur between more than two instances of types. For example, the same instance of an operation of a class may be used as an operation of two or more state transitions, or in some state transition diagrams also as operations of states (Rumbaugh et al. 1991, Booch and Rumbaugh 1995). Here the same value is referred to by property types of multiple non-property types. To distinguish the states and related operations of a single object from the operations needed in communication between several objects, some techniques (e.g. OSA, Embley et al. 1992) include separate relationship types, or even techniques, for this purpose.

4) Dependence on other instances. The dependent type can not have other property values than those already defined in other type instances. For example, in UML all objects must be connected to a related class by their name and therefore it should not be possible to create an object which is not instantiated from the defined class. As a result, an object can not refer to classes which are not yet defined. A similar kind of polymorphism exists in MOSES (Henderson-Sellers and Edwards 1994) between a ‘message’ relationship type used in an event model and a ‘service’ of a class used in an O/C model. Thus, in a metamodel, a property type of a message called ‘message name’ must share values already defined as values of the property type ‘service name’. In other words, an object should not call for a method of another object which is not available in the called object.

Dependency is optional in many polymorphism structures. For example, the balancing rules in Yourdon (1989a, p 281) between names of entities and data stores do not state which of these must be defined first as long as the names match in the end. In contrast, methods which propose some guidance for applying different types in a specific order require that the dependency is defined. For example, in ISAC (Lundeberg et al. 1981) a ‘data element’ instance in a data structure diagram is normally defined only after the related ‘data set’ instance is defined in a D-graph (i.e. the name of a data element refers to the name of a data set). Thus, the procedural part defined in a process model of an ISD method usually requires as a counterpart a specific static structure (Kinnunen and Leppänen 1994, Jarke et al. 1998).

In addition to the identification of various structures of polymorphism, each type of polymorphism must be defined according to its scope and type of checking. The scope of the polymorphism defines the space from which the property type instances can be shared. Based on the polymorphism structures found, all three scopes are possible. The method level includes all instances of the property types. For example, in UML ‘class’ has a property type named ‘category’ for specifying to which category a class belongs. The possible values for the ‘category’ are the names of all categories defined in all category diagrams or class diagrams. Similarly, an object may be characterized by the name of an existing class (e.g. Walden and Nerson 1995, Booch and Rumbaugh 1995). Polymorphism restricted to the scope of a model limits the possible shared instances into those defined in a single model. For example, according to the balancing rules of SA/SD (Yourdon 1989a), actions of state transitions must correspond to the name of the flows defined in a related data flow diagram in which the control process is described. The most complex form of polymorphism is based on a dependency on a specific instance of a given type in contrast to all instances, or instances of a single model. Among the methods modeled their dependency can be found from explosion or from composite objects (Venable 1993). For example, a state diagram of a single object (instance of a class) can have only those actions as a property of transition, which are also used for an object. In other words, the dynamic behavior described in a state transition diagram can have only those actions defined as operations of the related class in the class diagram. Similarly, a state can have as a property only those actions which are defined in the related class (Rumbaugh et al. 1991), and the attribute name of an object must match one in its class (Booch and Rumbaugh 1995, p 5). In our metamodel-based definition of UML, this would require that state variables defined as ‘values’ in our metamodel would be related to the attribute definitions of a class.

The checking of polymorphism can be either active or passive depending on the dependency of polymorphism, i.e. dependent or independent. Dependent polymorphism implies active checking, as it can be checked at all times that a created or modified type can not have other values than those defined already (i.e. no new values are created). Independent polymorphism can also be checked actively if the modeling tool informs the modeler of the available instances of other property types which a created or modified type could use as instances of its property types. Active checking, however, would necessitate that the polymorphism would be satisfied at all times. For example, according to the balancing rules in Yourdon (1989a) it would not be possible to create an entity if a data store with the same name would exist and vice versa. Thus, independent polymorphism must apply passive checking.

Modeling of method knowledge has been recognized as one of the main research problems in the field of method engineering (e.g. Kumar and Welke 1992, Kronlöf 1993, Brinkkemper 1996). In this section we have approached this problem in an inductive manner by analyzing modeling techniques from 17 different ISD methods, modeling them into metamodels and adapting them into CASE environments. This analysis has pointed out various patterns, categories and rules of methods that a metamodeling language should capture to model method knowledge more completely. These were generalized into metamodeling requirements by specifying constructs for metamodeling languages which extend existing semantic data models (i.e. metametamodels in the context of metamodeling).

Although the identification of the essential metamodeling constructs is based on the examination of 17 ISD methods, we see several ways to explore these constructs further. The first and most obvious way is to enlarge the set of ISD methods analyzed. Second, the types of methods included could also be extended from analysis and design methods into other methods of ISD, like project management, programming languages, etc. This is especially important since most methods modeled follow the icon-link structure typical in CASE tool related methods. It would also be relatively easy to propose a method which could not be described with the proposed metamodeling constructs. This means that we can not exclude certain metamodeling construct, but rather only describe those which were needed for our metamodeling effort. Third, the metamodels of the software design oriented methods could be extended towards programming languages, as suggested in some references (c.f. Booch and Rumbaugh 1995). This would raise new requirements for metamodeling, especially related to data types to satisfy the grammatical rules of programming languages, as well as analysis of designs by executing or compiling them.

Finally, other metamodeling constructs could also be identified by analyzing metamodeling carried out in practice. For example, in three metamodeling experiments, 75% of the concepts identified were involved in specialization hierarchies (Wijers 1991, p 174). Although we acknowledge the usefulness of inheritance to simplify metamodels and organize elements of metamodels into more manageable hierarchies (Rossi and Tolvanen 1995) we did not include it among the essential constructs of a metamodeling language for one simple reason: all static knowledge of methods could be described without inheritance. Furthermore, in the metamodeling literature a variety of approaches are proposed for using inheritance: Oei and Falkenberg (1994) propose a metamodel hierarchy for organizing techniques and building transformations between them, Elmasri et al. (1985) apply inheritance for entity types, Kelly et al. (1996) apply inheritance for other types as well as object types, and Venable (1993) and Ebert et al. (1996) extend inheritance to also cover the relationships that the object type participate in. The limitation on describing method knowledge only as it is represented in the literature is recognized in Chapter 6: we apply a metamodeling language together with the proposed extensions to describe method knowledge based on situations and experiences of method use (i.e. also in practice rather than just from the method literature).