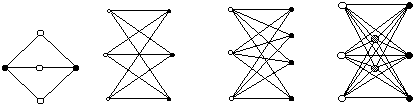
Kaksijakoisen verkon solmut voidaan jakaa kahteen joukkoon siten, että kaikki verkon välit ovat ainoastaan näiden joukkojen yhdysvälejä. Joukkojen sisällä ei ole siis sellaisia solmuja, joilla on yhdistävä väli. Kaksijakoisessa verkossa voi välien määrä olla enintään {v/2}*(v-{v/2}) kun {v/2} esittää suurinta kokonaislukua, joka on pienempi kuin v/2. Jos kaikki välit, joilla nämä kaksi alijoukkoa voidaan yhdistää kuuluvat kaksijakoiseen verkkoon G niin kyseessä täysin (maksimaalinen) kaksijakoinen verkko. Tällöin käytetään merkintää G = K_m,n, missä m ja n ovat alijoukkojen solmujen määrät.

Verkko on k-jakoinen jos sen solmut voidaan samoin jakaa k:hon toisensa poissulkevaan osajoukkoon siten että minkään välin molemmat päätesolmut eivät kuulu samaan joukkoon ja minkään osajoukon solmujen välillä ei ole välejä. Vastaavasti kuin edellä voidaan määritellä täysin k-jakoinen verkko. Esimerkiksi täysin kolmijakoisesta verkosta käytetään merkintää K_m,n,q.