Täydellinen verkko
on verkko, jonka jokaisesta solmusta on väli verkon jokaiseen muuhun solmuun. Täydellisestä verkosta jossa on v kpl solmuja käytetään merkintää Kv.Täydellisessä verkossa välien määrä on e = (v-1) + (v-2) +...+ 1 = (v-1) + (v-2) + ...+ (v - (v-1)) + (v-v) = (v + v +...+ v) -[1 + 2 + ... (v-1) + v] = vv-v(v+1)/2 = (v
2-v)/2.Samaan päästään huomioimalla, että jos verkon kaikkien
solmujen astelukujen summaa, S deg(v), merkitään A:lla niin A = 2e. Jos solmujen määrä on v niin on yhden solmun asteluku v-1 ja näin ollen A = v(v-1). Siis e=1/2v(v-1).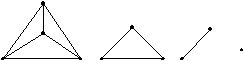
Täydelliset tasoverkot
Täydellisiä tasoverkkoja, jotka sisältävät kaikkia tasoverkon perusyksiköitä solmuja, välejä ja alueita, jotka on piirretty niin sanotulle tavalliselle tasolle, on täsmälleen kaksi kappaletta ja ne ovat molemmat kolmioverkkoja (kuva yllä). Myös kaksi solmua ja niiden väli sekä yksi solmu ilman väliä mahtuvat rajatapauksina tällaisten täydellisten verkkojen kategoriaan. Toisin ilmaistuna ainoat täydelliset verkot, jotka voidaan upottaa tasolle ovat K
v, kun v = 1, 2, 3 tai 4. Eräs verkkoteorian perustuloksista, tunnettu Kuratowskin lause, antaakin rajoituksen: "verkko on tasoverkko jos ja vain jos yksikään sen aliverkoista ei ole homeomorfinen verkolle K5 (tai K3,3).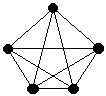
Kuratowskin verkko
K5Yllä oleva johtaa helposti ajatukseen, että kaikki kaksiulotteisille pinnoille piirretyt täydelliset verkot olisivat kolmioverkkoja. Sama ajatus tulee mieleen katsottaessa täydellisiä verkkoja, joissa jokaisen kolmen solmun joukon solmut voidaan liittää toinen toisiinsa kolmella välillä. Esimerkkikuvassamme on toinen tunnetuista Kuratowskin verkoista eli K
5 (toinen on kaksijakoinen K3,3). On kuitenkin mahdollista piirtää myös täydellisiä neliö-, viisiö-, kuusio- jne. verkkoja, kun otetaan käyttöön pallopintaa monimutkaisemmin kaareutuvia kaksiulotteisia topologisia pintoja, jotka määrittelee Eulerin luku E = 2 - 2g.Tavalliselle pallopinnalle E=2 koska
g = 0.