TIES411 - Piirreavaruudet, kvantisointi, segmentointi ja mean shift
* Huom. Tämä on kesken ja ei tule todennäköisesti ikinä olemaankaan valmis.*
Aihe
Kuvan segmentointi tarkoittaa kuvan jakamista erillisiin alueisiin visuaalisen samankaltaisuuden perusteella. Segmentoinnin käyttötarkoitus konenäössä on yksinkertaistaa kuva-esitystä helpommin käsiteltäväksi. Aiemmassa tutoriaalissa tutkimme erilaisten ruuvien ja muttereiden erottamista toisistaan tasaista taustaa vasten ja havaitsimme, että niiden tunnistaminen esimerkiksi silhuetin perusteella on melko yksinkertaista ja haluaisimme soveltaa tätä tietoa monimutkaisempiin kuviin. Toisinsanoen, haluamme jakaa kuvia visuaalisesti samankaltaisiin alueisiin ja täten yksinkertaistaa koko kuvan analysoimisen yksittäisten alueiden analysoimiseksi.
Kahdessa edellisessä tutoriaalissa törmäsimme kuvapiirteen käsitteeseen. Mittasimme yksinkertaisia piirresignaaleja eri tavoin eri osista kuvaa. Eräs motivaatio tälle on se, että yksittäiset kuvat sisältävät yksinkertaisesti liikaa informaatiota, jotta siitä saisi mitään tolkkua. Sen sijaan, kuten ihmisaivotkin, että katsomme pikseleitä numeroina, tutkimme reunoja, kuvan karkeutta, tummuutta tai kappaleen muotoja. Tässä tutoriaalissa paneudumme tarkemmin piirreavaruuden käsitteeseen ja sen käyttöön segmentoinnissa.
Piirre-avaruuksista filosofisesti..
Usein on helpompaa tarkastella, kuvien sijaan piirreavaruuksia, joissa kuva tai sen osat esitetään sen sisältöä kuvaavina piirrevektoreina, kuten esimerkiksi silhuettikuvista irroitettujen kappaleiden muotopiirteinä tai kuvan eri osista laskettuina tekstuuripiirteinä. Tämä esitys poikkeaa kurssin alkupuolen tavasta katsoa kuvaa signaalina. Tiheän, jatkuvan funktion sijaan tarkastelemme laihoja joukkoja sopivissa avaruuksissa.
Piirreavaruuksilta on hyvä toivoajoitain ominaisuuksia. Haluaisimme mieluusti, että piirreavaruudet olisivat vähintään täydellisiä (semi)normiavaruuksia, jotta iteratiiviset menetelmämme konvergoisivat ja jotta voisimme verrata eri piirteitä toisiinsa.
Tässä tutoriaalissa käytämme varsin alkeellisia piirreavaruuksia, mutta pyrimme löytämään menetelmiä, jotka toimivat yhtä hyvin erilaisten piirteiden muodostamilla avaruuksilla.
RGB- ja LAB-piirreavaruudet
Ensimmäinen esimerkki piirreavaruudesta on tuttu kuvapisteiden rgb-värikolmikkojen avaruus ja siihen liittyvä piirrekuvaus \(F_{rgb} : \mathbb{Im} \rightarrow \text{RGB}=(\left\{mathbb{R^3}\right\},\|\cdot\|_{rgb})\)
\(F_{rgb}(I) = \left\{ \left[\begin{array}{c} R(I(x,y))\\G(I(x,y))\\B(I(x,y))\end{array}\right] \bigg| (x,y) \in \text{dom}(I) \right\}\),
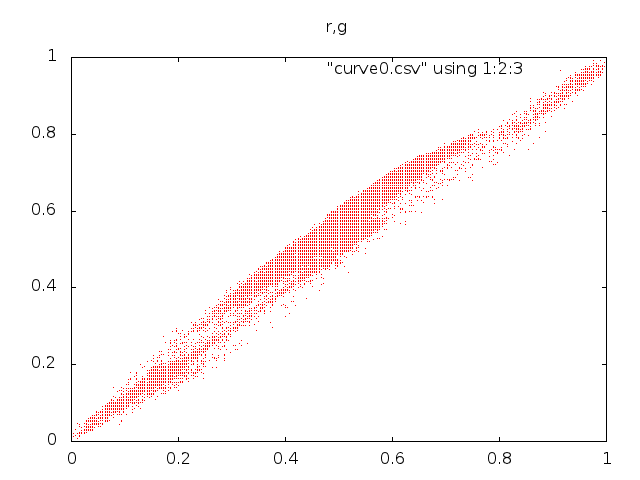
Esimerkkikuvan esitys RGB-piirreavaruudessa näyttää tälle:
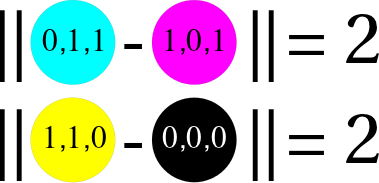
RGB-avaruudessa on kuitenkin yksi varteenotettava pulma, eli millainen on \(\|\cdot\|_{rgb}\)? Esimerkiksi tavallinen euklidinen normi \(\|x\|_2 = \sqrt{R(x)^2+G(x)^2+B(x)^2}\) ei vastaa juuri ollenkaan näkemystämme siitä, miten samankaltaisia värit ovat. Esimerkiksi molemmat seuraavista väripareista ovat tämän normin mielessä yhtä erilaisia:
Ei ole ollenkaan selvää, millainen metriikka tulisi valita, jotta se vastaisi havaintoamme. Yksi mahdollinen valinta on käyttää RGB väriavaruuden sijaan Lab-väriavaruutta, joka vähintäänkin pyrkii vastaamaan havaintoamme tavallisen normin mielessä.
\(F_{LAB} : \mathbb{Im} \rightarrow \text{LAB}=(\left\{\mathbb{R^3}\right\},\|\cdot\|_2)\)
\(F_{LAB}(I) = \left\{ \left[\begin{array}{c} L(I(x,y))\\a(I(x,y))\\b(I(x,y))\end{array}\right] \bigg| (x,y) \in \text{dom}(I) \right\}\),
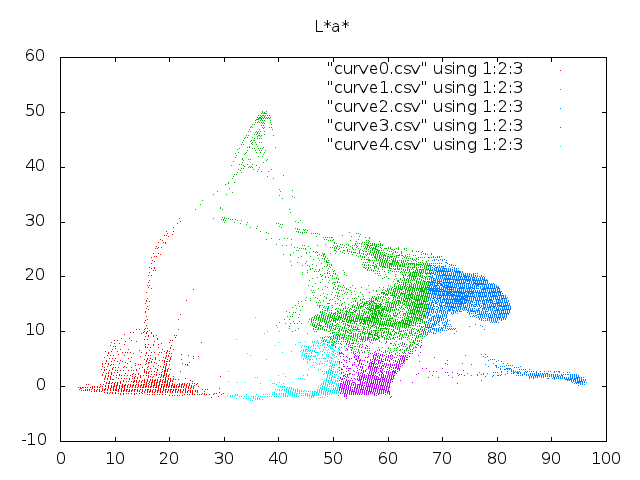
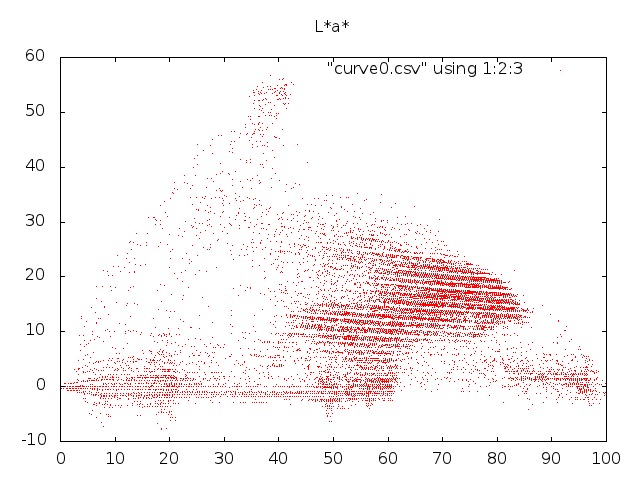
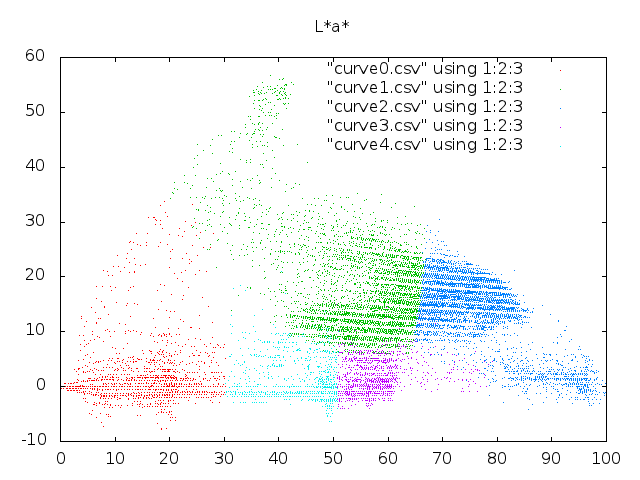
Esimerkiksi edellisen väriparin syaanin ja purppuran välinen ero on LAB avaruudessa noin 81 yksikköä ja keltaisen ja mustan 123 yksikköä, eli vähintään tässä yksittäistapauksessa LAB vastaa havaintoamme paremmin. Jos tarkastelemme sitä, mitä esimerkkikuvamme näyttää tässä avaruudessa, yllätymme iloisesti, sillä piirreavaruuden pisteillä on selkeä rakenne ja hetken päästä käy ilmi, että piirreavaruuden tihentymät vastaavat eri kuvakohteita ja että meillä on useampiakin keinoja löytää piirreavaruutemme rakenteita.
.
Voimme myös muodostaa yksi-ulotteisen piirreavaruuden harmaasävykuville (\(L\)).
Tehtävä – LAB vs RGB
- Etsi yksi sadoista netin värimuunnoslaskureista
- Piirrä mieluisiasi väriläiskiä ja mittaa niiden etäisyyksiä sekä LAB:ssä että RGB:ssä. Vastaako kumpikaan intuitiota?
S-piirreavaruus ja tuloavaruudet
Tarkastellaan seuraavaksi piirreavaruutta, jolla ei yksinään ole merkityksellistä rakennetta, mutta, joka luo sellaista muihin piirreavaruuksiin, nimittäin pikseliavaruuden koordinaattien avaruutta (\(S=\) engl. Spatial, tila):
\(F_{s} : \mathbb{Im} \rightarrow \text{S}=(\mathbb{R^2},\|\cdot\|_2)\)
\(F_{s}(I) = \left\{ \left[\begin{array}{c} x\\y\end{array}\right] \bigg| (x,y) \in \text{dom}(I) \right\}\),
Tämä kuvaus muodostaa digitaalisten kuvien tapauksessa useimmiten suorakaiteen muotoisen tasavälisen hilan, jonka merkitys syntyy silloin, kun se yhdistetään esimerkiksi väriavaruuden kanssa:
\(F_{S \times \text{LAB}} : \mathbb{Im} \rightarrow S\times \text{LAB}=(\mathbb{R^2},\|\cdot\|)\)
\(F_{S \times \text{LAB}}(I) = f_{s}(I) \oplus f_{\text{lab}}(I) = \left\{ \left[\begin{array}{c} x\\y\end{array}\right] \bigg| (x,y) \in \text{dom}(I) \right\}\).
On sanomattakin selvää, että \(S \times \text{LAB}\) on isomorfinen alkuperäisen kuvan kanssa. Mielenkiintoiseksi tämän tarkastelun tekee oikean normin valinta tälle avaruudelle: Montako metriä vastaa punaisen ja sinisen värisävyn eroa? Tälläisissä tuloavaruuksissa joudumme aina käsittelemään eri komponentit sovelluskohtaisesti.
Avaruuksien rakenteesta – K-Means algoritmi
Koska havaitsimme, että piirreavaruudessamme on rakennetta, niin lienee luonnollista pyrkiä selvittämään, että millaista. Yleisellä tasolla tätä ongelmaa kutsutaan tiedonlouhinnaksi (datamining, ks. tiedonlouhintakurssi) ja sitä voidaan lähestyö useilla eri tavoilla. Yksi näistä on K-means klusterointi, jossa pyritään jakamaan piirreavaruuden pisteet osajoukkoihin \(S_i\) siten, että pisteiden etäisyydet joukkojen keskipisteisiin \(\mu_i\) ovat keskimäärin mahdollisimman pieniä. Toisinsanoen, haluamme siis minimoida suureen:
\(\underset{\mathbf{S}} {\operatorname{arg\,min}} \sum_{i=1}^{k} \sum_{\mathbf x_j \in S_i} \left\| \mathbf x_j - \boldsymbol\mu_i \right\|_2^2\)
Tämän minimointitehtävän ratkaiseminen ei näytä helpolle, sillä mahdollisia jakoja eri joukoiksi on noin \(N!\) kappaletta! Ongelma on kuitenkin hyvä esimerkki NP-täydellisestä ongelmasta, jolle on olemassa tehokas ja käytönnössä toimiva heuristinen ratkaisu. Ratkaisu on peräisin henkilöltä Stuart Lloyd ja vuodelta 1957, ja se menee näin:
Valitse mielivaltaiset klustereiden keskipisteet \(\mu_i\)
Jaa pistejoukot keskipisteiden kesken asettamalla kukin piste lähimmän keskipisteen määräämään joukkoon.
Laske näin syntyneiden joukkojen keskipisteet ja jatka kohdasta 1.
Parin kierroksen jälkeen jaot eivät enää muutu ja ratkaisu on syntynyt.
Edellä löytämämme \(\text{LAB}\)-piirreavaruuden k-means klusterit näyttävät tältä:
ja jos olemme pitäneet yllä tietoa siitä, mistä pikselikoordinaateista kukin piirrepiste on näytteistetty, niin voimme esittää klusteroinnin tuloksen myös kuvana:
Tuloskuvassa samankaltaiset värit ovat päätyneet samoihin ryhmiinsä, mutta kuten jo piirreavaruuskuvasta nähdään, niin osa klustereista on hajonnut kahtia. Tämä näkyy tuloskuvassa kohdehenkilön kasvoissa ja taustassa.Tähän on kaksi eri syytä:
K-Means pyrkii havaitsemaan olennaisesti symmetrisiä klustereita ja jakamaan avaruuden näiden mukaan monikulmioihin. Meidän klusterimme eivät ole symmetrisiä.
Emme mitenkään ota huomioon pikseleiden keskinäisiä etäisyyksiä ja menetelmä saattaa ryhmittää tyystin eripuolilla kuvaa olevia kuvapisteitä samaan ryhmään ja vastaavasti vierekkäisiä pisteitä eri ryhmiin.
Ensimmäiselle kohdalle emme voi tehdä paljoakaan, mutta toinen kohta on helposti korjattavissa: tarkastellaan kuvaa avaruudessa \(S\times \text{LAB}\), joka sisältää tiedon myös pisteiden sijainneista..
.. ja tuloksena on iloinen monikulmiokuva, sillä \(\|\cdot\|\) metriikka ei ole järjellinen tässä avaruudessa. Ongelman ydin on siinä, että pisteiden väriarvot, joiden etäisyyksien erot ovat välillä \([0..100]\) vaikuttavat pisteiden etäisyyksiin enemmän, kuin pisteiden väliset etäisyydet, jotka vaihtelevat välillä \([0..400]\).
Jos väriarvo ei vaikuta paljoakaan piirreavaruuden pisteiden etäisyyksiin, niin se ei myöskään vaikuta paljoa klusteroinnin tuloksiin. Joudumme siis valitsemaan piirreavaruuden, jonka metriikkaa vastaamaan enemmän intuitiotamme siitä, milloin pisteet ovat lähellä toisiaan. Sopivan avaruuden löytäminen on valitettavasti täysin tapauskohtaista. Usein riittää valita avaruus, jossa aineistomme täyttää avaruuden mahdollisimman tasaisesti. (Eli voimme vaikkapa skaalata piirreavaruuden kaikki koordinaatit datan mukaan \([0,1]\)-välille). Tässä tapauksessa valitsemme sopivan hihavakion ja avaruuden, jossa pistekoordinaattien vaikutus etäisyyteen on pienempi:
\(F(I) = \left\{ \left[\begin{array}{c} L(I(x,y))\\a(I(x,y))\\b(I(x,y))\\\frac{1}{10}x\\\frac{1}{10}y\\\end{array}\right] \bigg| (x,y) \in \text{dom}(I) \right\}\),
ja saamme seuraavan tuloksen:
Sovellus – Gaussinen siloitus ja Bilateraalinen siloitus
Muotoillaan seuraavaksi tuttu gaussinen siloitus piirreavaruuden operaatioksi ja yleistetään siitä ns. bilateraalinen suodatus, jolla on useita hyviä ominaisuuksia. Kuten aiemmasta muistamme Harmaasävykuvan \(I\) diskreetti konvoluutio gaussisella ytimellä \(G\) on:
\((*) : (\text{Im},\text{Im}) \rightarrow \text{Im}\)
\(\begin{align*} \left[I*G_{\sigma}\right](i,j) & = \sum_{u,v} G(i−u, j−v) I(u,v) \\ \end{align*}\)
Voidaanko vastaava operaatio määritellä piirreavaruuteen \(S\oplus L\)? Helposti, sillä havaitsemme, että konvoluution laskeminen voidaan tehdä, että summaamme jokaiseen kuvapisteeseen sijoittu kopio ytimestä kerrottuna kyseisen kuvapisteen arvolla. Tällä tavalla ajateltuna ‘konvoluution’ laskeminen ei edellytä lähtöjoukolta tiheää rakennetta ja koska avaruus \(S\oplus L\) on isomorfinen alkuperäisen kuvan kanssa, niin voimme laskea konvoluution kuvaamalla pisteet ensin piirreavaruuteen, laskea ‘’konvoluution’’ siellä ja kuvata tulospisteet takaisin kuvaksi.
\((*) : (S\oplus L,(\mathbb{N} \times \mathbb{N})\rightarrow\mathbb{R}) \rightarrow \text{Im}\)
\(\begin{align*} \left[I*G_{\sigma}\right](s) & = \left[I*G_{\sigma}\right]((i,j),k) \\ & = \sum_{((u,v),l) \in F_{S\times L}(I)} G((u,v)-(i,j)) k\\ & = \sum_{(x,l) \in F_{S\times L}(I)} g(\|x-y\|_2) k\\ \end{align*}\)
Edellä olemme merkinneet koordinaatteja \((i,j)\) \(y\):llä, summauspistettä \(x\):llä. Koska ydin on symmetrinen, voimme esittää sen yksi-ulotteisen profiilin ja normin yhdisteenä. Toisinsanoen, ydin \(G\) on tässä tapauksessa eräänlainen ‘samankaltaisuusmittari’, jolla vertaamme kuvapisteiden koordinaatteja. Voimme toki ottaa huomioon myös värierot, jolloin saamme, samalla kaavalla, bilateraalisen suotimen \(B_{\sigma_s\sigma_l} : (S\times L,(\mathbb{N} \times \mathbb{N})\rightarrow\mathbb{R}) \rightarrow \text{Im}\)
\(\begin{align*} \left[B_{\sigma_s\sigma_l}(I)\right](s) & =\left[B_{\sigma_s\sigma_l}\right](I)]((i,j),k) \\ & =\sum_{(x,l) \in {S\times L}(I)} g_{\sigma_s}(\|x-y\|_2) g_{\sigma_l}(|k-l|) l\\ \end{align*}\)
Tässä tapauksessa käytämme eri ydintä sävyarvoille ja pikselietäisyyksille, sillä niiden välinen yhteys on riippuvainen kuvasta. Havaitsemme myös heti, että sama ajatus toimii kaikissa muissakin piirreavaruuksissa, ja voimme tehdä saman suodatuksen esimerkiksi avaruudessa \(S\times\text{LAB}\). Bilateraalinen suodin on erittäin käyttökelpoinen kuvankäsittelytyökalu, sillä se poistaa tehokkaasti kohinaa, mutta säilyttää kappaleiden reunat tarkempina kuin gaussinen siloitus.
Tehtävä – Parempi kuvanterävöitys.
- Selvitä, mitä on
unsharp masking ja testaa sitä jollekin kuvalle. Mitä tapahtuu kappaleiden reunoille, jos käytetään liian voimakasta maskia?
- Korvaa em. menetelmässä gaussinen suodatus bilateraalisella. Mitä havaitset.
Seuraavaksi olemme tietysti kiinnostuneita siitä, miltä muutos näyttää piirreavaruudessa. Sovelletaan bilateraalista suodatusta pari kertaa alkuperäiseen kuvaan,
ja kuvataan se piirreavaruuteen:
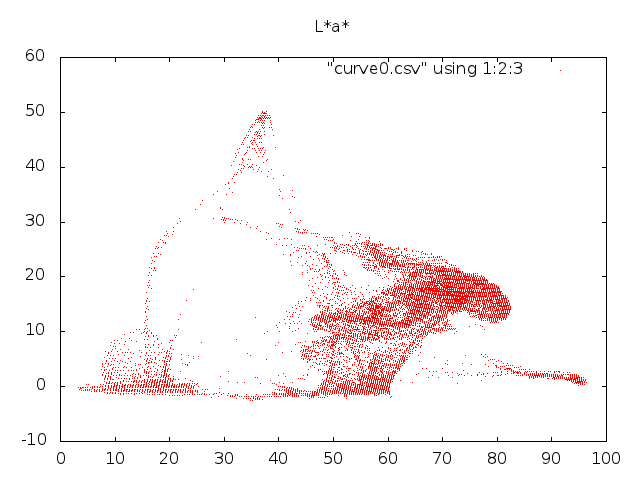Havaitaan, että rakenteet piirreavaruudessa ovat vahvistuneet, sillä kuva on käynyt läpi prosessin, jossa samankaltaiset piirteet siirtyvät lähemmäksi toisiaan.
Tästä herää tietysti toive, että kuvan voisi segmentoida K-means algoritmilla paremmin kuin aiemmin, mutta edelleen pulmana on se, että piirreavaruuden klusterit eivät muodosta K-meansin toivomia symmetrisiä klustereita:
Seuraa kuitenkin kysymys, että mitä tapahtuisi, jos jatkaisimme piirreavaruuden puristamista bilateraalisen suodatuksen kaltaisella operaatiolla, kunnes klusterit olisivat tihentyneet suunnilleen yhdeksi pisteeksi?
Mean Shift – Eräs lähestymistapa piirreavaruusanalyysiin
Tämä tutoriaalinosa pohjautuu artikkeleihin Mean Shift: A Robust Approach Toward Feature Space Analysis ja Mean Shift, Mode Seeking, and Clustering.
Meanshift algoritmi on eräs, erittäin yksinkertainen menetelmä, jolla voidaan käsitellä piirreavaruuden pistepilviä. Se menee näin:
- Valitaan aloituspiste \(y_0\).
Seuraava iteraatiopiste saadaan valitsemalla pisteet, jotka ovat riittävän lähellä pistettä \(y_{i-1}\) ja laskemalla niiden painopiste (ts. keskiarvo). Muotoillaan tämä taas piirreavaruuden kautta:
\(y_i = \frac{\sum_{x\in s}{K(x-y)x}}{\sum_{x\in s}{K(x-y_{i-1})}} = y_{i-1} + (m(y_{i-1})-y_{i-1})\),
missä etäisyyskriteeri on määritelty ytimen \(K\) kautta:
\(K(x)=\begin{cases} 1, \text{kun } \|x\| \leq \lambda \\ 0, \text{muuten.} \end{cases}\)
Toistetaan kunnes \(\|y_i - y_{i-1}\|\) on sopivan pieni.
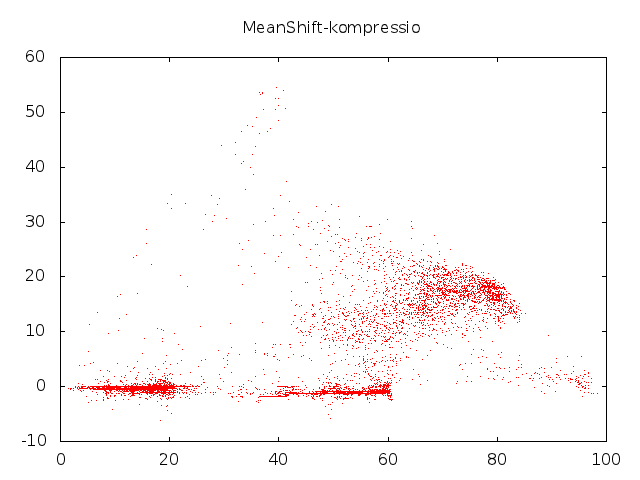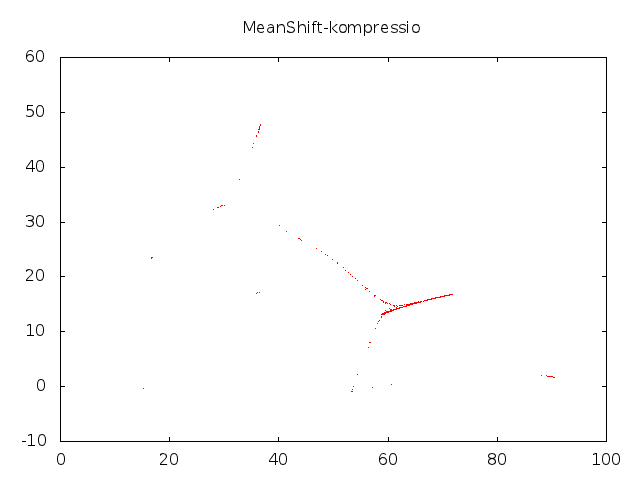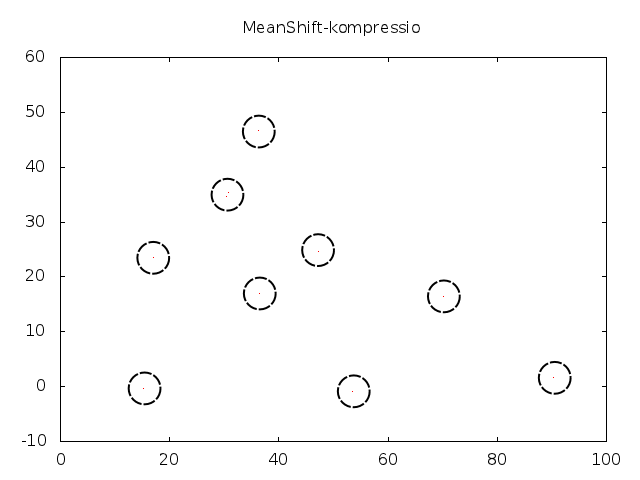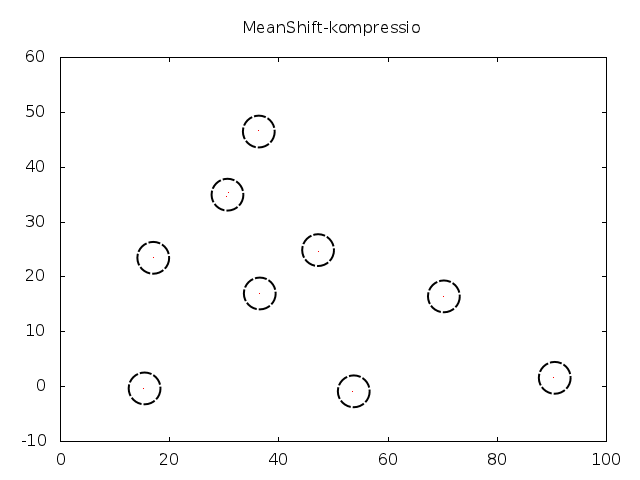
Voidan osoittaa, että tämä prosessi konvergoi ja konvergenssipiste on datapisteiden estimoidun tiheysfunktion moodi. Toisinsanoen, jos suoritamme tätä prosessia kaikille pisteille, niin lopputulos on se, että pisteet kerääntyvät tiheiksi klustereiksi:
Koska jokainen klusteri on tihentynyt käytännössä yhdeksi pisteeksi, voimme helposti määrätä kuvalle segmentoinnin käyttäen näitä pisteitä. Naiivi algoritmitoteutus vertaa useita kertoja jokaista kuvapistettä jokaiseen toiseen kuvapisteeseen, joten käytämme pienennettyä kuvaa. (Reaaliaikaversiosta puhumme parin viikon päästä.)
Tässä vaiheessa herää viimeistään kysymys siitä, että mistä on kysymys. Menetelmä on toki yksinkertainen, mutta mitä se tekee?. Yksi mahdollinen selitys saadaan muotoilemalla ongelma tiheysjakaumaestimaatin avulla:
Kernel Density Estimation
Ajatelkaamme piirreavaruuden pisteitä jonkin prosessin tuottamina näytteinä reaalimaailman kappaleesta ja jos meillä on useampia kuvia samasta kappaleesta, niin saamme oletettavastikin yhä tiheämpiä pistepilviä. Nyt, jos valitsemme piirreavaruudesta jonkin mielivaltaisen pisteen, niin kuinka todennäköisesti löytyy siitä piirrejoukosta joka syntyy kun otamme uuden kuvan alkuperäisestä kappaleesta?
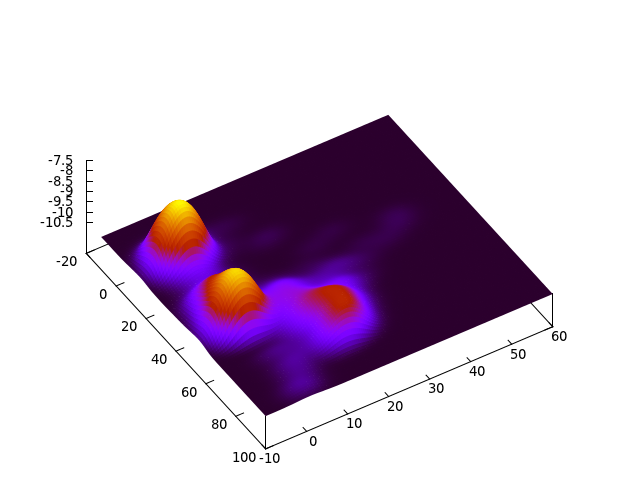
Luonnollisesti voimme olettaa, että mikäli valitsemme pisteen piirreavaruuden tiheästä kohdasta, niin sellaisen löytäminen on todennäköisempää, kuin jos valitsemme pisteen sieltä, missä niitä ei ennestään ole. Toisinsanoen, näytteistysprosessimme tuotokset noudattavat jotain todennäköisyysjakaumaa ja kysymykseemme vastaa tämän jakauman tiheysfunktio:
Seuraavaksi teemme oletuksen, että jakauma on syntynyt useammasta kuvassa näkyvästä kohteesta. Yksi kohde on esimerkiksi kuvan henkilön takki (vasen nurkka tiheysestimaatissa) ja toinen on tausta (keskellä). Nyt jos palaamme alkuperäiseen intuitioon siitä, että haluaisimme manipuloida piirreavaruutta siten, että sen tihentymät kutistuisivat yksittäisiksi pisteiksi (jotka olisivat siis helppo erottaa toisistaan), huomaamme, että tuollaiseksi pisteeksi sopisi esimerkiksi yo. jakauman moodit / huiput.
Ensiksi kuitenkin lyhyesti se, miten tiheysestimaatin voi muodostaa. Yksi tapa tähän on Kernel-Density-Estimation tai Parzenin ikkuna, joka on yksinkertaisuudessaan häikäisevä:
\(\hat{f}_K(x) = \frac{1}{nh^d}\sum_{i=1}^{n}K \left(\frac{x-x_i}{h}\right)\),
missä \(n\) on näytepisteiden määrä, \(K\) on sopiva ydinfunktio, ja \(h\) sen skaalauskerroin, jolla voimme määritellä, kuinka laajoja klustereita oletamme löytävämme. Selvästi on kelvollinen tiheysfunktio, eli se on positiivinen, ja sen integraali on 1, mikäli ydinfunktion integraali on 1 ja se on sekä symmetrinen, että yksihuippuinen. Yksi yleinen ja helppo ydinfunktio on tuttu gaussin funktio:
\(K_N(x) = (2\pi)^{-d/2}\exp\left(-\frac{1}{2} \|x\|^2\right)\).
Ensimmäinen havainto on, että gaussisella ytimellä tämä on sama asia kuin aiemmin nähty gaussinen siloitus piirreavaruudessa! Ainoa ero on tulkinnassa, on se, että nyt meillä on jatkuva funktio yli koko piirreavaruuden. Jos oletamme jälleen että ydin \(K\) voidaan esittää profiilinsa avulla muodossa \(ck\left(\|x\|^2\right)\), saamme
\(\hat{f}_K(x) = \frac{c}{nh^d}\sum_{i=1}^{n}k\left(\|\frac{x-x_i}{h}\|^2\right)\),
Tämän funktion gradientti on ketjusäännön ja summan lineaarisuuden nojalla
\(\nabla\hat{f}_K(x) = \frac{2c}{nh^{d}}\sum_{i=1}^{n}(x-x_i)k'\left(\|\frac{x-x_i}{h}\|^2\right)\).
Merkitsemme ytimen profiilin derivaattaa (jonka oletamme olevan siisti ja olemassa) merkinnällä \(-g(x)=k'(x)\), niin
\(\begin{align} \nabla\hat{f}_k(x) &= \frac{2c}{nh^{d}}\sum_{i=1}^{n}(x_i-x)g\left(\|\frac{x-x_i}{h}\|^2\right) \\ &= \frac{2c}{nh^{d}}\left[\sum_{i=1}^{n}g\left(\|\frac{x-x_i}{h}\|^2\right)\right] \left[\frac{\sum_{i=1}^n x_ig\left(\|\frac{x-x_i}{h}\|^2\right)} {\sum_{i=1}^n g\left(\|\frac{x-x_i}{h}\|^2\right)} - x\right] &= \left[\hat{f}_g(x)]\right] \left[m(x)\right] \end{align}\)
nyt havaitsemme, että
\(\nabla\hat{f}(x) = \hat{f}(x)\frac{2c}{nh^{d}}m(x).\)
Toisinsanoen \(m(x)\) on siis karkeasti muotoa
\(m(x) = \frac{1}{2}h^2*\textbf{c}\frac{\nabla\hat{f}_K(x)}{\hat{f}_g(x)\frac{2c}{nh^{d}}}\).
Toisinsanoen, edellä mainittu mean shift vektori \(m(x)\) osoittaa aina tiheysestimaatin gradientin, tai maksimaalisen kasvun suuntaan. Jakaja on myös tärkeä, sillä mitä harvemmassa pisteet ovat, sitä vähemmän mielenkiintoisesta alueesta on kyse, ja sitä nopeammin sieltä voidaan edetä pois. Toisinsanoen, mean shift on itseasiassa gradienttimenetelmä tiheysfunktion huippujen löytämiseksi!
Tästä saamme heti pari parannusta mean shift menetelmään, sillä oletettavastikin, tasajakautunut ydin, minkä pohjalle menetelmämme rakensimme, ei ole paras vaihtoehto. Mutta nyt ylläoleva tarkastelu antaa mahdollisuuden käyttää mitä tahansa yksihuippuista, ykköseksi integroituvaa funktiota, jonka osaamme derivoida. (Toisinsanoe, käytämme siis aina ja ikuisesti funktiota \(\exp\left(\frac{1}{2}x\right)\), sillä tietoteknikkoina emme osaa derivoida juuri mitään muutakaan.)
Sovellus – Liikkuvan kohteen seuraaminen mean shift menettelyllä
Eräs tavanomainen sovellus mean shiftille on käyttää sitä liikkuvan kohteen seuraamiseen:
Liikkuvan kohteen seuraaminen olisi täysin triviaali tehtävä, jos osaisimme luotettavasti tunnistaa seurattavan kappaleen kaikista videokuvista. Valitettavasti esimerkiksi yhden ihmisen tunnistaminen ihmisjoukosta tai edes sekavasta taustasta aiheuttaa usein paljonkin harhahavaintoja. Oletetaan kuitenkin, että meillä on jonkinlainen tapa karakterisoida sitä, millä todennäköisyydellä kohde saattaisi kussakin pisteessä olla.
Seuraamistehtävässä oletamme myös, että alkutilanne on tunnettu: haluamme seurata kohdetta, joka on ajanhetkellä \(t\) kohdassa \(x\). Nyt voimme käyttää mean shiftiä, sillä jostain pisteestä liikkeelle laskettuna se hakee lähimmän moodin näytteiden tiheysjakaumaestimaatista. Lisäksi tiheysjakaumaestimaatti voidaan rakentaa eri skaaloilla, valitsemalla kerroin \(h\) (yllä) sopivasti, joten jos tiedämme kappaleemme koon, voimme valita myös sopivan skaalan.
Toisinsanoen, mean shift annettua pistettä lähinnä olevan, todennäköisimmän havainnon kohteesta. Kohteen seuraaminen koostuu siis siitä, että otamme edellisen havainnon ja kuvasarjan seuraavan kuvan ja meanshiftaamme havaintomme uuteen sijaintiin. Menetelmä on lisäksi hyvin nopea, sillä mean shiftaamme yhtä pistettä per seurattava kohde ja voimme hyvin käyttää kuvan paikkatietoa hyväksi ja käsitellä vain pientä ikkunaa alkuperäisen havainnon ympäriltä.
Eräs tapa etsiä kohdetta on mitata kohteen värien tiheysfunktio \(\text{kde}_{\text{target}}\) (tai, tehokkuutta halutessa, värijakauma) ja laskea jokaiselle kuvapisteelle kohteen tiheysfunktion arvo (ts. kuinka todennäköisesti tämän värinen piste löytyy kohteesta):
\(F_{\text{prob}}(x,y) = \text{kde}_{\text{target}}(F (x,y))\)
Tämän jälkeen voimme soveltaa mean shiftiä ajattelemalla, todennäköisyyttä painokertoimena (Ts. yksittäisen pisteen sijaan, meillä on nyt todennäköisyys sille, että piste on kussakin paikassa):
\(y_i = \frac{\sum_{x\in s}F_{\text{prob}}(x){K(x-y)x}}{\sum_{x\in s}{K(x-y_{i-1})}} = y_i - m(y_{i-1})\).
Sovellus – Kohinan poisto mean shift menettelyllä
Voimme myös käyttää mean shiftiä kuvan siloittamiseen soveltamalla sitä piirreavaruuteen \(S\times \text{LAB}\). Menettelyn idea on se, että otamme jokaista kuvapistettä vastaavan piirreavaruuden pisteen, meanshiftaamme sen alkuperäisessä pistepilvessä ja katsomme minkä värinen piste meille syntyy prosessin lopuksi. Uusi kuva koostuu siis vanhoista kuvakoordinaateista, mutta uusista väreistä:
Meanshift muistuttaa siis tässä tapauksessa bilateraalista suodinta, jonka maski liikkuu suodatuksen aikana. Jälleen, tehokkuuden takia voimme rajoittaa meanshiftin melko pieneen ikkunaan kohdepisteen ympärille. Kuitenkin, mitä suurempaa skaalaa käytämme, sitä tasaisempi tuloksesta tulee.
Tehtävä – Kokeile
Testaa tässä tutoriaalissa esitettyjä menetelmiä erilaisiin kuviin, eri parametreillä ja kirjoita havaintojasi ylös. Palauta pull-requestina yousourcesta.
Tehtävä – Kappaleiden ryhmittely
Koska piirreavaruuskäsite on joustava, me voimme soveltaa tämän tutoriaalin menetelmiä hyvin laaja-alaisesti. Voimme esimerkiksi ryhmitellä toissakertojen ruuveja tai tai edellistutoriaalin pistepilviä. Kokeile meanshift klusterointia valitsemalla esimerkiksi kirjainmerkkeihin MNIST tietokannassa ja katso millaisen ryhmityksen saat muodostettua.
