Aihe

Tutustutaan kaksiulotteiseen Fouriermuunnokseen. Fouriermuunnos on erinomainen matemaattinen työkalu, jonka avulla voidaan kattavasti ymmärtää monia konenäön ongelmia. Toisaalta, Fouriermuunnos, ja erityisesti sen diskreetti ja nopea versio, fast fourier transform (FFT), on hyödyllinen myös käytännöllisenä menetelmänä.

Tämän tutoriaalin aikana ymmärrämme mistä konvoluutio-operaatio on peräisin ja sen miten näytteistetty signaali käyttäytyy ja osaamme muuttaa kuvien kokoja oikein.

Siirtoinvariantit lineaariset systeemit

Useimmat kuvantamisjärjestelmät ja -systeemit käyttäytyvät pitkälti siten, että niillä on kolme tärkeää ominaisuutta:

• Superpositioperiaate: Oletetaan, että \(R( f + g) = R( f ) + R(g)\) eli syötteiden summan vaste on erillisten vasteiden summa.

• Skaalautuvuus: Nollasyötteen vaste on nolla, ja skaalatun syötteen vaste on skaalattu versio alkuperäisen syötteen vasteesta, eli \(R(k f ) = kR( f )\) Systeemi joka toteuttaa superpositioperiaatteen ja on skaalautuva on lineaarinen.

• Siirtoinvarianttius: Siirtoinvariantissa systeemissä vaste siirrettyyn syötteeseen on alkuperäisen syötteen vasteen vastaava siirtymä. Kameran tapauksessa tämä tarkoittaa yksinkertaisesti esimerkiksi sitä, että jos keskelle kameran näkökenttää asetettu pieni valopiste näkyy kameran ottamassa kuvassa keskellä kuvaa kirkkaana läiskänä, ja valopistettä siirretään reunaa kohti, tulisi kuvassa näkyä edelleen sama läiskä siirtyneenä.

Laitetta, järjestelmää tai systeemiä joka on lineaarinen ja siirtoinvariantti kusutaan lineaariseksi siirtoinvariantiksi laitteeksi, järjestelmäksi tai systeemiksi. Tässä on tärkeää on se, että lineaarisen siirtoinvariantin systeemin vaste annettuun syötteeseen saadaan määrättyä konvoluution avulla. Tämä seikka todennetaan systeemeille, joiden syötteet ja vasteet ovat diskreettejä (lukuvektoreita tai taulukkoja).

Tehtävä

• Osoita, että konvoluutio on siirtoinvariantti
• Osoita, että konvoluutio on skaalautuva

Diskreetti konvoluutio

Tarkastellaan tilannetta ensin yksiulotteisessa tapauksessa ja oletetaan, että on annettu lineaarinen siirtoinvariantti systeemi jonka syötteet ja vasteet ovat vektoreita ja oletetaan myös että syöte- ja vastevektorit sisältävät (numeroituvasti) äärettömän määrän alkioita. Täten voidaan toistaiseksi välttää pienet tarkennusta vaativat seikat syötteiden ja vasteiden alku- ja loppukohdissa. (Ks. Edellinen tutoriaali ja reunailmiöt)

Yksiulotteinen diskreetti konvoluutio

Oletetaan, että on annettu syötevektori \(f\) , joka on ääretön ja indeksoitu kokonaisluvuilla (eli on olemassa \(-1\):s alkio jne.) ja jonka \(i\):nnettä alkiota merkitään \(f_i\):llä, \(i = \dots − 2, −1, 0, 1, 2 \dots\). Syötevektori \(f\) voidaan esittää painotettuna summana kantavektoreista. Sopivat kantavektorit ovat sellaisia, joiden yksi alkio on arvoltaan 1 muiden ollessa arvoltaan 0. Merkitään \(ei = \dots 0, 0, 1, 0, 0 \dots\) joka on siis vektori jonka alkio \(i\) on 1 muiden alkioiden ollessa 0.

Määritellään seuraavaksi siirto-operaattori \(\text{Shift}( f , i)\), joka palauttaa vektorin jonka \(j\):s alkio on vektorin \(f\) alkio \(j−i\): \(\text{Shift}(f , i) j = f(j−i)\). Esimerkiksi vektorin \(\text{Shift}(e_0 , 1)\) alkio numero 1 on 1, ja muut alkiot ovat nollia. Siirto-operaattorin avulla vektori \(f\) voidaan esittää kantavektorin \(e_0\) avulla seuraavasti:

\(f = \sum_i f_i(\text{Shift}(e0 , i)\).

Merkitään lineaarisen siirtoinvariantin systeemimme vastetta syötevektoriin f merkinnällä \(R( f )\). Koska systeemi on siirtoinvariantti, täytyy olla voimassa

\(R(\text{Shift}( f , k)) = \text{Shift}(R( f ), k)\),

ja lisäksi koska se on lineaarinen on voimassa

\(R(k f ) = kR(F)\) \(R( f + g) = R( f ) + R(g)\).

Nämä seikat yhdessä tarkoittavat sitä, että

\(\begin{align*} R( f ) &= R\left(\sum_i f_i \text{Shift}(e_0, i)\right) \\ &= \sum_i R(f_i \text{Shift}(e_0, i)) \\ &= \sum_i f_i R(\text{Shift}(e_0, i)) \\ &= \sum_i f_i (\text{Shift}(R(e_0), i)) \end{align*}\)

Tästä seuraa, että voimme määrätä systeemin vasteen mihin tahansa datavektoriin \(f\) , kunhan vain tunnemme sen vasteen vektoriin \(e_0\) . Tätä vastetta \(R(e_0)\) kutsutaan yleensä systeemin (yksikkö)impulssivasteeksi. Yksikköimpulssivasteita mitataan monista laitteista. Näitä mm. kultakorvahifistit tutkailevat tarkasti vahvistintestiraporteista ja päättelevät laitteen sopivuutta oman laitteiston osaksi.

Merkitään nyt systeemin yksikköimpulssivastetta \(g = R(e_0)\). Nyt siis

\(R( f ) = \sum_i f_i \text{Shift}(g, i) = g ∗ f\).

Tämä määrittää yksiulotteisen diskreetin konvoluutio-operaation, jota merkitään operaattorisymbolilla \(∗\). Jos tarkastellaan vasteen \(R( f )\) alkiota \(j\), saadaan lauseke

\(R( f ) j = \sum_i g_{j−i} f_i\),

joka on analoginen aiemman kaksiulotteisen konvoluutiolausekkeen kanssa, ja itse asiassa selittää sen alkuperän. Lineaarisen siirtoinvariantin systeemin vaste syötteeseen saadaan siis konvoluutio-operaatiolla syötteestä ja systeemin yksikköimpulssivasteesta.

Kaksiulotteinen diskreetti konvoluutio

Tässä tapauksessa sekä syöte että vaste ovat äärettömiä kaksiulotteisia taulukoita, joiden rivejä ja sarakkeita indeksoidaan kokonaisluvuin. Merkitään tällaisen taulukon \(F\) alkiota \(i, j\) F(i, j):llä. Kaksiulotteisessa diskreetissä tapauksessa yksikköimpulssi on ääretön taulukko E, jonka alkiot ovat kaikki nollia paitsi \(E(0,0) = 1\). Jos \(G = R(E)\) on systeemin \(R\) yksikköimpulssivaste, johtaa vastaava päättely kuin edellä yksiulotteisessa tapauksessa tulokseen, jonka mukaan systeemin vaste syötteeseen F on

\(\left[R(F)\right](i, j) = \sum_{u,v} G_{i−u,j−v} F_{u,v} = G ** F = G * F.\)

Merkinnällä ** täsmennetään kyseessä olevan kaksiulotteinen konvoluutio-operaatio, silloin kun on epäselvyyttä käsitelläänko yksi, vai kaksiulotteisia signaaleja.

Fourier muunnos

Edellä käytettiin temppua, jossa signaali \(f(x, y)\) esitettiin painotettuna summana hyvin suuresta (tai äärettömästä) määrästä hyvin pieniä (tai äärettömän pieniä) laatikkofunktioita. Tämä tapa korostaa ajatusta siitä, että signaali on vektoriavaruuden alkio, eli vektori. Laatikkofunktiot muodostavat erään kannan tähän vektoriavaruuteen ja painokertoimet muodostavat vektorin alkioittaisen esityksen tässä “laatikkokannassa”. Tarvitsemme vielä uuden työkalun käsitelläksemme jäljellä olevat kaksi avointa kysymystä:

• Vaikka onkin selvää, ettei kuvan diskreetti pikselirepresentaatio voi sisältää jatkuvan kuvasignaalin kaikkea informaatiota, emme vielä tiedä mikä osa informaatiosta katoaa.

• On myös selvää, ettemme voi tiputtaa diskreetin pikselirepresentaation re- soluutiota yksinkertaisella tavalla ottamalla mukaan vain joka k:nnen pikselin (shakkilaudan kuvasta voisi tulla kokomusta tai kokovalkoinen). Kuinka resoluutiota sitten turvallisesti ja minimivahingoin pudotetaan?

Nämä molemmat avoimet ongelmat liittyvät kuvasignaalissa esiintyviin nopeisiin muutoksiin. Esimerkiksi resoluution pudottaminen alkeellisesti saattaa hukata nopeita vaihteluita, koska ne tapahtuvat matalaresoluutioversioon valittujen pikselien välisessä osassa alkuperäistä dataa.

Koska voimme tulkita kuvasignaalimme vektoriavaruuden alkioina, voimme myöskin tehdä vektoriavaruuteen kannanvaihdon, ja tutkia saman signaalin esitystä uudessa kannassa. Sopiva uusi kanta koostuu jatkuvassa tapauksessa äärettömästä määrästä eri suuntiin etenevistä ja eri taajuisista sinitasoaalloista. Kun signaali esitetään tällaisessa kannassa, on nopeasti muuttuva informaatio helppo havaita, sillä korkeataajuisia tasoaaltokantavektoreita vastaavat signaalivektorin alkiot ovat tällöin suuria. Palautetaan mieliin siis Fouriermuunnoksen perusteet signaalinkäsittelyn kurssilta, ja päivitetään tiedot kaksiulotteiseen tapaukseen.

Eri suuntaan eteneviä, eri taajuuksisia siniaaltoja (ks.koodi)

Yksiulotteisessa tapauksessa diskreetti fouriermuunnos kuvaa (yksiulotteisen, diskreetin) signaalin aika-avaruudesta taajuusavaruuteen,

\(\left[F(x)\right](k) = \sum_{n=0}^{N-1} x(n) \cdot e^{-i 2 \pi \frac{k}{N} n}\),

ja vastaava käänteismuunnos,

\(\left[F^{-1}(x)\right](n) = \frac{1}{N} \sum_{k=0}^{N-1} \left[F(x)\right](k) \cdot e^{+i 2 \pi \frac{n}{N} n}\)

palauttaa signaalin aika-avaruuteen.

Kuvien tapauksessa kyseessä on kaksiulotteinen signaalin muunnos, jolloin puhumme aika-avaruuden sijaan tila-avaruudesta (engl. spatial domain). Kuvan fouriermuunnos voidaan määritellä helposti 1D-signaalin muunnoksen kautta: Kiinnitetään ensin x-koordinaatti ja lasketaan fouriermuunnos y:n suhteen, jolloin saadaan sarakkeittainen fouriermuunnos. Tämän jälkeen suoritetaan 1D muunnokset x:n suhteen, ja lopputuloksena saadaan koko kuvan fourier muunnos.

\(\left[F_{2D}(I)\right](x,y) =\sum_{i=0}^{W-1} \left(\sum_{j=0}^{H-1} I(x,y) \cdot e^{-i 2 \pi \frac{j}{N} n}\right) \cdot e^{-i 2 \pi \frac{i}{N} n} = \sum_{i=0}^{W-1} \sum_{j=0}^{H-1} I(x,y) \cdot e^{-i 2 \pi\left(\frac{kx}{W}+\frac{yj}{H}\right)}\),

Samoin kuin yksiulotteisella, niin myös kaksiulotteisella fouriermuunnoksella on monia näppäriä ominaisuuksia, esimerkiksi (Todistukset signaalinkäsittelyn kurssilla):

Näistä tärkein lienee viimeinen muunnospari, jota kutsutaan konvoluutioteoreemaksi ja sen avulla voidaan laskea tehokkaasti suuria konvoluutioita.

Tehtävä - Erilaisten kuvien Fouriermuunnoksia

Tarkastellaan joidenkin yksinkertaisten funktioiden kosinimuunnoksia. Alla oleva ohjelma generoi ja piirtää kuvia, jotka on sämplätty erilaisista yksinkertaisista funktioista.

import WebTools
import CV.DFT
import CV.Pixelwise
import CV.ColourUtils
import CV.ImageMathOp
import CV.Transforms

piirraDFT = logarithmicCompression . fst . dftSplit . dft
main = webCreate "kosiniviivat" $ montage (2,7) 5
   [
   g (50,50), piirraDFT (g (50,50))
   , g (30,30) #+ g (70,70), piirraDFT (g (30,30) #+ g (70,70))
   ,kosinix, piirraDFT kosinix
   ,kosiniy, piirraDFT kosiniy
   ,vino, piirraDFT vino
   ,ikkunoitu, piirraDFT ikkunoitu
   ,kiekko, piirraDFT kiekko
   ]
 where 
   koko@(lev,kor) = (100,100)
   kiekko,kosinix,kosiniy,vino :: Image GrayScale D32
   g :: (Int,Int) -> Image GrayScale D32
   g  (u,v)= imageFromFunction koko (\(x,y) -> exp(-0.02*(fromIntegral (x-u)**2 
                                                             + fromIntegral (y-v)**2)))
   kosinix = imageFromFunction koko (\(x,y) -> cos (0.5*fromIntegral x))
   kosiniy = imageFromFunction koko (\(x,y) -> cos (0.5*fromIntegral y))
   vino    = imageFromFunction koko (\(x,y) -> cos (0.2*fromIntegral (x+y)))
   kiekko  = imageFromFunction koko (\(x,y) -> if ((x-lev`div`2)^2 + (y-kor`div`2)^2) < 350
                                               then 1 else 0)
   ikkunoitu    = imageFromFunction koko (\(x,y) -> hann (x,y) * cos (0.2*fromIntegral (x+y)))
   hann (x,y) = 0.5 * (1-cos(2*pi*fromIntegral x/(fromIntegral lev-1)))
                    * (1-cos(2*pi*fromIntegral y/(fromIntegral kor-1)))

• Selitä, miksi edellisten kuvien fouriermuunnos on sellainen kuin se on.

Tehtävä - Suodatus fouriermuunnoksella

Seuraavaksi tarkastellaan millaisia operaatioita fouriermuunnoksen avulla on helppo määritellä. Esimerkiksi siloitusoperaatio voitaisiin nähdä siten, että kuvasta poistetaan kaikki korkean taajuuden komponentit.

1. Selvitä, mitä kuvalle tapahtuu, kun seuraavia operaatioita sovelletaan kuvan fouriermuunnokseen.

• \(\left[A f\right](x,y) = \begin{cases} f(x,y) & \text{, jos } ||x-y||<30 \\ 0 & \text{, muuten} \end{cases}\)
• \(\left[B f\right](x,y) = \begin{cases} f(x,y) & \text{, jos } ||x-y||>30 \\ 0 & \text{, muuten} \end{cases}\)

3. Seuraavassa kuvassa esitetään pahasti pilalle mennyt kuva. Käytä fourieranalyysiä ja palauta se mahdollisimman ennalleen:

import WebTools
import CV.Filters
import CV.Matrix as M
import CV.ColourUtils

main = web "aallot" "images/FourierSmall.jpg"  f
 where
   f :: Image GrayScale D32 -> Image GrayScale D32
   f kuva = stretchHistogram (remapImage corrupt kuva)
   corrupt f (x,y) = f (x,y) + sin(7*fromIntegral x + 5*fromIntegral y)
                                 - sin(0.1*fromIntegral x - 0.3*fromIntegral y)

Esimerkki: silmälasien välttämättömyys

Konvoluutioteoreeman ja toiseksi viimeisen taulukkorivin muunnosparin avulla saamme idealisoidun matemaattisen todistuksen sille miksi silmälasit ovat välttämättömät taittovirheestä kärsiville! Taittovirheen takia kohde ei tarkennu täsmälleen verkkokalvolle vaan se tarkentuu joko verkkokalvon eteen tai taakse. Kummassakin tapauksessa yksittäinen piste projisoituu verkkokalvolle kiekoksi, jota tässä approksimoidaan laatikkofunktiona.

Hajataitto

Taittovirheinen silmä on siis tässä eittämättä hieman keinotekoisessa esimerkissä lineaarinen siirtoinvariantti systeemi, jonka hypoteettinen yksikköimpulssivaste on \(g(x, y) = R(\delta(x, y))= \text{box}_1 (x) \text{box}_1 (y)\). Systeemin vaste syötteeseen saatiin yksikköimpulssivasteen ja syötesignaalin \(f (x, y)\) konvoluutiona. Konvoluutioteoreeman mukaan vastaava tulos saadaan kertomalla syötteen Fourier-muunnos yksikköimpulssivasteen Fourier-muunnoksella ja ottamalla tuloksesta käänteismuunnos

\(\begin{align*} f(x, y)∗∗g(x, y) &= F^{-1} \left(\left[F f\right](x,y))\left[F g\right](x, y)\right) \\ &= F^{-1} \left(\left[F f\right](x, y) \frac{\sin(\pi u)}{\pi u} \frac{\sin(\pi v)}{\pi v}\right). \end{align*}\)

Koska funktio \(\sin(x)/x\) saa arvon \(0\) kun \(x = \dots − 2 \pi, −\pi, \pi, 2\pi \dots\) kuvautuu osa alkuperäisen signaalin Fourier-kertoimista nollaksi. Tämä on peruuttamaton vahinko, sillä alkuperäistä informaatiota ei voi enää tämän jälkeen palauttaa takaisin.

Esimerkki (Tähti): CSI-jekku

Jos silmälasit ovat välttämättömiä, niin onko mitään tehtävissä, jos kuvaan on eksynyt sumentumaa? Ehkäpä vähän, sillä jos tiedämme tai arvaamme, että on sumentuman yksikköimpulssivaste on \(S\), niin silloinhan pätee

\(I_\text{havainto} = I_\text{Oikea}**S\)

jolloin konvoluutioteoreeman nojalla,

\(F(I_\text{havainto}) = F(I_\text{Oikea})F(S)\)

mikä voidaan jakaa alkioittain \(F S\):llä,

\(F(I_\text{havainto})/F(S) = F(I_\text{Oikea})\)

ja kaavan oikealle puolelle jää mukavasti alkuperäinen kuva. Tässä on tietysti se ongelma, että oletamme, että \(F S\) on kaikkialla jotain muuta kuin nolla, mitä se ei useinkaan ole (ks. ed. esimerkki). Voimme kuitenkin määritellä estimaatin \(S^-1_\text{est}\)

\(S^{-1}_\text{est}(u,v) = \begin{cases} 1/\left[F(S)\right](u,v) & \text{jos } |\left[F(S)\right](u,v)| > t \\ 0 & \text{muuten} \end{cases}\)

minkä jälkeen

\(F(I_\text{est}) = F(I_\text{Havainto})(S^{-1}_\text{est})\)

ja

\(I_\text{est} = F^{-1} (F(I_\text{Havainto})S^{-1}_\text{est})\).

Hetken puuhastelu paljastaa nopeasti, että tämä toimii melkein kuin CSI:ssä, jos valitsee kuvan ja sumentuman oikein, ja aika kehnosti lähes kaikissa käytännön tilanteissa.

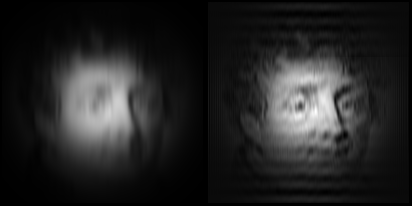
CSI on paljastanut syyllisen: J.Fourier

Tehtävä: Turhaudu CSI jekkuun

1. Edellä herra fourier epäsumennettiin tällä ohjelmalla. Saatko säädettyä siihen sopivan yksikköimpulssivasteen, että seuraava matemaatikko saadaan selvennettyä?

Alfred Haar

Näytteistäminen

Näytteistämisella tarkoitetaan jatkuvan signaalifunktion arvojen keräämistä diskreetin hilan hilapisteissä. Yksiulotteisessa tapauksessa signaalifunktio on kuvaus reaaliluvuilta reaaliluvuille, ja näytteistäminen tarkoittaa diskreetin arvojoukon poimintaa tällaisesta kuvauksesta diskreetissä määrittelyjoukon pisteistössä. Tärkein erikoistapaus on kerätä näytteet tasaväliseltä pisteistöltä, joten voimme olettaa että näytteet kerätään reaalilukuakselin kokonaislukupisteissä. Tämä tarkoittaa sitä, että käytössämme on operaatio \(\text{Sample}_{1d}\) , jonka syöte on funktio \(f\) ja joka palauttaa ko- konaisluvuilla indeksoitavan reaalilukuvektorin \(k\) :

\(k = \text{Sample}_{1d}(f)\), \(k_i = f(i)\), i = − 2, −1, 0, 1, 2 $

Kaksiulotteinen tapaus on hyvin samankaltainen kuin yksiulotteinen. Vaikka näytteistys voisikin perustua epäsäännölliseen hilaan (kuten silmän verkkokalvolla), jatkamme sillä oletuksella, että näytteet kerätään tason kokonaislukukoordinaattipisteissä. Tämä on myös hyvä malli useimmille digitaalisille kameroille. Lopulliset näytteistetyt kuvat ovat suorakulmaisia äärellisen kokoisia kaksiulotteisia taulukoita, sillä kuva-alue on tällainen ja sen ulkopuolella näytteitä ei oteta (näytearvot asetetaan nolliksi). Kaksiulotteinen näytteistys voidaan esittää operaation \(\text{Sample}_{2d}\) avulla. Tämän syöte on funktio \(F(x, y)\) reaalilukutasolta reaalilukuakselille ja se palauttaa kaksiulotteisen taulukon \(K_{i, j}\) jonka sekä rivejä, että sarakkeita indeksoidaan kokonaisluvuilla:

\(K = \text{Sample2d}F\), \(K_{i, j} = f(i, j)\), \(i, j = \dots − 2, −1, 0, 1, 2 \dots\)

Näytteistetyn signaalin integroituva malli

Tarvitsemme jatkoanalyysia varten integrotuvan mallin näytteistetystä signaalista. Tätä tarvitaan erityisesti Fourier-muunnosta varten, jossa mallimme ja kompleksisen eksponenttifunktion lausekkeen tulo täytyy pystyä integroimaan. Signaalin integraalin tulisi selvästikin yhtyä sen näytearvotaulukon alkioiden summaan. Emme siis voi mallittaa näytteistettyä signaalia funktiona, jonka arvo on nolla, paitsi kokonaislukukoordinaattipisteissä joissa sen arvo olisi näytearvo, koska tällaisen funktion integraali olisi 0 (Asiasta tarkemmin kurssilla Mitta- ja Integraaliteoria).

Aiemmin esitetyllä \(\delta\)-funktiolla on tärkeä ominaisuus, jota voidaan hyödyntää integroituvan mallin muodostuksessa:

\(\begin{align} \int_{-\infty}^{infty} a\delta(x)f(x) dx &= a \lim_{\epsilon\rightarrow 0}\int_{-\infty}^{infty} \frac{\text{box}_\epsilon}{\epsilon}f(x) dx\\ &= a \lim_{\epsilon\rightarrow 0}\sum_{i=-\infty}^{infty} \frac{\text{box}_\epsilon}{\epsilon}f(i\epsilon) \text{Shift}(\text{box}_{\epsilon},i\epsilon)\epsilon\\ &= a f(0) \end{align}\)

eli \(\delta\)-funktion ja jatkuvan funktion f tulon intergaalin arvo on \(f(0)\) Tästä saamme soveliaan mallin: asetamme jokaiseen näytteistyspisteeseen \(\delta\)- funktion, jonka arvoa painotamme pisteeseen liittyvällä näytearvolla. Tämä saadaan aikaan kertomalla näytteistetty signaali joukolla \(\delta\)-funktiota, joita on yksi per näytepiste. Näin ollen voimme uudelleen määritellä näytteistysoperaattorin yksiulotteisessa tapauksessa:

\(\left[\text{Sample}_{1d}(f)\right](x) = \sum_{i=-\infty}^\infty f(i)\text{Shift}(\delta(x),i)=f(x) \sum_{i=-\infty}^\infty \delta(x-i)\)

Summalauseketta \(\sum_{i=-\infty}^\infty \delta(x-i)\) kutsutaan (ilmeisestä syystä) kampafunktioksi (engl. comb function). Sen kaksiulotteinen vastine on n.s. “naulasänkyfunktio” (engl. bed-of-nails function) jonka avulla kaksiulotteinen näytteistäminen voidaan muotoilla seuraavasti:

\(\left[\text{Sample}_{2d}(f)\right](x) = \sum_{i=-\infty}^\infty\sum_{j=-\infty}^\infty F(i,j)\delta(x-i,y-j) = F(i,j)\sum_{i=-\infty}^\infty\sum_{j=-\infty}^\infty\delta(x-i,y-j)\)

Molemmilla näytteistysoperaattoreilla on nyt haluttu ominaisuus: ne palauttavat integroitavan “otuksen”, jonka integraalin arvo on näytearvojen summa.

Kampafunktio

Piikkimattofunktio

Aliasoituminen

Oletettavastikin informaatiota katoaa näytteistyksen yhteydessä. Näytämme miten liian hitaasti/harvasti näytteistämällä saatu näytearvojoukko tulkitsee alkuperäistä jatkuvaa signaalia väärin: Alkuperäisen signaalin korkeataajuiset spatiaaliset taajuuskomponentit ilmenevät matalataajuisina spatiaalisina taajuuskomponentteina näytteistetyssä signaalissa. Tämä ilmiö tunnetaan nimellä aliasoituminen.

Näytteistetyn signaalin Fourier-muunnos

Aiemmin johdimme näytteistetylle signaalille mallin, joka saadaan kertomalla alkuperäinen jatkuva signaali naulasänkyfunktiolla. Konvoluutioteoreeman mukaan tämän tulon Fourier-muunnos on näiden kahden funktion Fourier-muunnosten konvoluutio. Aiemmin esitetyn mukaan naulasänkyfunktion Fourier-muunnos on toinen, taajuustason naulasänkyfunktio. Funktion konvoluutio naulasänkyfunktion kanssa muodostaa summan naulasänkyfunktion \(\delta\)-piikkeihein siirretyistä funktion kopioista. Tässä tapauksessa konvoluutio lasketaan siis alkuperäisen signaalin Fourier-muunnoksen kanssa ja efekti on se, että tuloksena saadaan siirrettyjä Fourier-muunnoksia jotka summataan yhteen: \(\begin{align*} F\left(\left[\text{Sample}_{2d}(f)\right](x,y)\right) &= F\left(F(x,y)\sum_{i=-\infty}^\infty\sum_{j=-\infty}^\infty \delta(x-i,y-j)\right) \\ &=F(u,v) ** F\left(\sum_{i=-\infty}^\infty\sum_{j=-\infty}^\infty \delta(x-i,y-j)\right) \\ &=F(u,v) ** \sum_{i=-\infty}^\infty\sum_{j=-\infty}^\infty \delta(u-i,v-j) \\ &=\sum_{i=-\infty}^\infty\sum_{j=-\infty}^\infty F(u-i,v-j) \end{align*}\)

missä funktion \(F(x, y)\) Fourier-muunnosta on merkitty \(F(u, v)\):llä.

Jos signaalin siirrettyjen Fourier-muunnosten kantajat eivät leikkaa toisiaan voidaan alkuperäinen signaali palauttaa täydellisesti takaisin leikkaamalla yksi Fourier-muunnoskopio talteen ja muuntamalla se takaisin käänteismuunnoksella. Kuitenkin usein käy niin, että siirrettyjen Fourier-muunnosten kantajat leikkaavat toinen toisiaan. Tällaisessa tapauksessa emme pysty palauttamaan alkuperäistä signaalia täydellisenä takaisin. Tämä johtuu siitä, että kantajien leikkausalueella on summautunut yhteen saman Fourier-muunnetun signaalin matala- ja korkeataajuiset kertoimet. Jos tunnetaan vain summan arvo, ei tästä tiedosta pysty yksikäsitteisesti päättelemään summautuneita termejä. Tämä ilmiö tapahtuu aina kun näytteenottotaajuus on alle kaksi kertaa signaalin sisältämä korkein taajuuskomponentti. Tämä tulos tunnetaan kirjallisuudessa Nyquistin teoreemana.

Karkea konseptikuva näytteistyksen vaikutuksesta fouriermuunnokseen

Tehtävä - Miltä näyttää pieleen menevä näytteistys?

1. Tarkastele kuvaa \(F(x,y) = \cos (x*k)\) eri k:n arvoilla, käyttäen esimerkiksi ohjelmaa Toy1. (Jos et saanut graphicstoolsia toimimaan, niin voit käyttää vaikkapa GHCi:tä lunttaamalla yo. ohjelmasta olennaiset kohdat). Ohjelmassa esiintyvä funktio imageFromFunction luo näytteistämää jatkuvan funktion naiivisti, kuten yllä esitetään. Mitä tapahtuu kun \(k\) kasvaa riittävän suureksi? Miten tämä ilmiö näkyy taajuustasossa?

2. Miten tämä ilmiö vaikuttaisi esimerkiksi valokuviin, joissa on verkkoaitaa tai tiiliseiniä?

Silottaminen ja uudelleennäytteistäminen

Nyquistin teoreema tarkoittaa, että on vaarallista pudottaa kuvan resoluutiota yksinkertaisesti ottamalla matalaresoluutiorepresentaation vain joka k:s pikseli (mikä huomataan edellisestä tehtävästä varsin nopeasti). Ennen kutistamista lähtökuva tulee alipäästösuodattaa siten, että sen ne spatiaaliset taajuuskomponentit, jotka taajuudeltaan ylittävät uuden näytteenottotaajuuden, poistuvat. Tämän voisi tehdä tarkasti kuvasignaalin Fourier-muunnoksen avulla nollaamalla kaikki Fourier-kertoimet \(F(u, v)\), jotka liittyvät liian korkeisiin taajuuksiin \(\sqrt{u^2 + v^2} > F_{tol}\) ja muuntamalla signaali käänteisellä Fourier-muunnoksella takaisin paikkatasoon. Yhtäpitävästi, muunnos olisi “mahdollista” tehdä suoraan paikkatasossa sellaisella konvoluutioytimellä \(G(x, y)\), jonka painokertoimet ovat muotoa \((sin x sin y)/(xy)\). Menetelmä ei kuitenkaan ole käytännöllinen, koska kyseisen painokerroinfunktion kantaja on ääretön (HT: Kuinka monta laskutoimitusta tarvitaan per kuva, jos tätä käytettäisi?).

Tärkein tapaus on se, että haluamme puolittaa sekä kuvan vaaka- että pystyresoluution. Oletamme, että alkuperäinen kuva ei ole aliasoitunut (jos se olisi, ei mitään olisi tehtävissä — kun kuva on alunperin näytteistetty on mahdollinen aliasoituminen jo tapahtunut). Näytteistetyn kuvan Fourier-muunnos koostuu nyt tason kokonaislukukoordinaattipisteisiin keskittyneistä Fourier-muunnoskopioista. Resoluution puolittaminen tarkoittaa sitä, että Fourier-muunnoskopiot keskittyvät tason pisteisiin, joiden koordinaatit ovat puolen yksikön monikertoja (tai vaihtoehtoisesti muunnokset efektiivisesti levittyvät kaksi kertaa laajemmalle alalle, koska puolta harvemmalla näytteenottotaajuudella aiempi korkein taajuus näyttäytyy efektiivisesti kaksi kertaa korkeampana). Tämä tarkoittaa myös sitä, että välttyäksemme aliasoitumiselta täytyy signaali ensin alipäästösuodattaa siten, että suodatuksen jälkeen signaalin korkein taajuus on enintään puolet aiemmasta korkeimmasta taajuudesta. Liiallista kaistan kavennusta tulee kuitenkin välttää, jottemme turhan paljon köyhdytä informaatiosisältöä.

Koska Gaussin ydin vaimenee nopeasti, ja Gaussin ytimen Fourier-muunnos on toinen, taajuustason Gaussin ydin, voi sitä käyttää käytännön approksimaationa ideaaliselle alipäästösuotimelle. Ytimen koon määräävän keskihajonnan \(\sigma\) valinta on sovelluskohtaista. Jos \(\sigma\) on suuri, täytyy maskinkin olla suuri, ja vaikka aliasoituminen onkin tällöin vähäistä (koska ytimen alkiot ovat taajuusrajan jälkeen hyvin pieniä) katoaa informaatiota sen takia, ettei ydin ole tasainen säilytettävän taajuusrajan alapuolella. Vastaavasti valitsemalla pieni \(\sigma\) säilyy informaation taajuusrajan alapuolella melko koskemattomana, mutta aliasoituminen voi olla runsaampaa. Valitsemalla aluksi \(\sigma = 1\) saa usein kelvon alkuarvauksen kokeelliseen keskihajonnan valintaan.

Tehtävä

Tarkastele edellisen tehtävän kuvaa siten, että näytteistäminen tapahtuu enemmän oikein.

1. Minkä kokoinen suodin tarvitaan kullekin kertoimelle \(k\)?
2. Kokeile koneella.

Vinkki: Voit joko laskea konvoluution \(F*G\) käsin ja syöttää sen tietokoneelle, tai laskea kuvan aluksi suuremmassa koossa, käyttää CV.Filters.Gaussian-funktiota ja sitten skaalata kuvan alkuperäiseen kokoon. Jokatapauksessa, joudut hieman miettimään miten asetat skaalat.

Tehtävä

Kuinka monta laskutoimitusta tarvittaisiin \(w\times h\) kokoisen kuvan suodattamiseen äärettömän kokoisella maskilla?