Kuvan olemus ja pisteittäiset operaatiot
Tällä kurssillä tarkoitamme kuvalla bitti- tai pikselikarttakuvaa, eli säännöllistä neliöhilaa, jonka solmukohtiin on tallennettu väri, tai harmaasävyarvoja. Toisinsanoen, puhumme enimmäkseen ihan tavallisista kuvista, joita liikkuu usein .jpg ja .png päätteisinä lähes kaikilla nettisivuilla ja jokaisessa digikamerassa.
Käytännössä kuvat talletetaan tietokoneen muistissa erilaisiksi taulukoiksi, mutta useimmiten niitä on järkevämpää käsitellä hieman abstraktimpina otuksina. Kurssin ohjelmiston näkökulmasta kuva on vain yksi abstrakti tietotyyppi, jolla on omat operaationsa ja sen sisäinen esitys “riippuu” tilanteesta. Kurssin matemaattisen tarkastelun osalta esitämme kuvat yleensä ns. indeksifunktioina \(\mathbb{N}^2 \rightarrow R\) tai erilaisten kantavektoreiden summina. On hyvä havaita, että molemmat ‘matemaattiset’ esitykset ovat myös toteutettavissa tietokone-ohjelmina, ja niistä saattaa olla apua algoritmien toteutuksen kannalta.
Tarkastellaan esimerkiksi synteettistä kuvaa yksikköpallosta:
\(F(x,y) = \begin{cases}1 &\text{jos }||(x,y)|| < 50 \\ 0 &\text{muuten} \end{cases}\).
Voimme luoda tälläisen kuvan yksinkertaisella ohjelmalla, joka on esitetty ao. kuvan yhteydessä. Tässä tapauksessa näemme kuvan siis ehdottomasti funktiona, emmekä taulukkona, ellemme sitten kiinnitä huomiota siihen ikävään seikkaan, että kuvat esitetään lähes poikkeuksetta siten, että origo on kuvan vasen ylänurkka ja kuvan akselit sojottavat alas ja oikealle.

import WebTools
import CV.Image
import CV.Pixelwise
main = webCreate "kiekko" kiekko
where
kiekko :: Image GrayScale D32
kiekko = imageFromFunction (150,150) f
f (x,y) | ((x-75)^2+(y-75)^2) < 50^2 = 1
| otherwise = 0
Tehtävä
- Piirrä neliö ja salmiakki.
- Piirrä kuva, joka on neliön ympyrän summa
- Piirrä kuva, joka on neliön ja ympyrän tulo.
Voimme myös nähdä kuvan skalaarina, eli eräänlaisena numeroa vastaavana otuksena, joita voidaan laskea yhteen, kertoa ja vähentää samaan tapaan kuin muitakin numeroita. Tässä tapauksessa tulkitsemme operaattorit \(\oplus \in \left\{+,-,*,/\dots\right\}\) siten, että operaatio sovelletaan erikseen jokaiselle kuvapisteelle:
\(\left[F \oplus G\right](x,y) = F(x,y) \oplus G(x,y)\).
Itseasiassa kaikkia skalaarifunktioita voidaan soveltaa samalla tavalla kuviin, esimerkiksi
\(\left[\sin(F)\right](x,y) := \sin\left(F(x,y)\right),\)
joskin niillä on harvemmin mitään järkevää käyttöä:

import WebTools
import CV.Image
import CV.Pixelwise
main = web "sinit" "images/FourierSmall.jpg" f
where
f :: Image GrayScale D32 -> Image GrayScale D32
f kuva = montage (2,1) 5 [kuva, mapImage s kuva]
s d = sin (8*d)
Tehtävä
- Yksi hyödyllinen operaatio on kuvan pikseliarvojen skaalaaminen näkyvälle \([0,1]\)-välille. Esimerkiksi edellinen \(\sin\)-esimerkki tuottaa väriarvoja väliltä \([-1,1]\), joten lopputulos ei näy oikein. Normalisoi yo. esimerkin tuloskuva oikealle välille. (Vinkki: “
import qualified CV.ImageMath as IM” ja käytä funktioita IM.minValue ja IM.maxValue.
- Sovella kokeeksi muitakin funktioita kuvaan.
Esimerkki: Kynnystys
Ehkä hyödyllisin pikseleittäinen operaatio on nimeltään kynnystys, ja se määritellään kuvalle \(f\) yksinkertaisimmillaan näin:
\(\left[T_t f\right](x,y)=\begin{cases} 1, &\text{ jos } f(x,y) < t\\ 0, &\text{ muuten,} \end{cases}\)
ja kuvalle se tekee näin:

import WebTools
import CV.Image
import CV.Pixelwise
main = web "kynnystys" "images/FourierSmall.jpg" f
where
f :: Image GrayScale D32 -> Image GrayScale D32
f kuva = montage (2,1) 5 [kuva, mapImage s kuva]
s d | d < 0.5 = 1
| otherwise = 0
Miksi kynnystys on niin merkittävä operaatio? Siksi, että se on yksinkertaisin mahdollinen operaatio, jolla kuvasta voidaan paikantaa erilaisia kohteita. Esimerkiksi punaisen pallon voi melko luotettavasti löytää valokuvasta kynnystämällä kuvan punaisen värikanavan ja monet teollisuussovellukset eivät tee mitään muuta kuin kuvaavat harmaata taustaa (liukuhihna, paperiraina, jatkuvan valu) ja kynnystävät siitä kohteita (Suklaanameja, paperin repeämiä, valuvirheitä) esille. Tietysti kuvan kynnystäminen suoraan ei useinkaan tuota järkevää tulosta, mutta erilaisten suodatusten jälkeen (ks. alla) sillä voi ratkaista mitä erilaisempia ongelmia.
Kynnystys on paljon tutkittu ala, ja erityisesti on epäselvää, miten kynnysarvo \(t\) tulisi valita, jotta vain haluttu kohde löytyisi. Menetelmiä on niin paljon kuin tekijöitäkin ja tässä vaiheessa riittänee todeta, että oikea valinta on aina tapauskohtainen. Yksi yleispätevä menetelmä on päättää mikä osuus kuvapisteistä on todennäköisimmin haluttua kohdetta ja asettaa raja sen mukaan:
\(t = \mu(f) + k\sigma(f) + \epsilon\),
eli asettaa rajaksi kuvapisteiden keskiarvo plus \(k\)-kertaa kuvapisteiden keskihajonta plus pieni toleranssi \(\epsilon\), joka hoitaa ne tapaukset, jolloin kuva on tyhjä.
Tehtävä
- Etsi netistä erilaisia kuvia ja kokeile keskiarvo+keskihajonta kynnystystä.
Lineaariset operaatiot
Useita tärkeitä kuvamuunnoksia voidaan tehdä saman yksinkertaisen konvoluutiomallin avulla. Tässä mallissa konstruoidaan uusi kuva siten, että uuden kuvan pikseleiden arvoiksi asetetaan painotettu summa käsiteltävän kuvan vastaavan pikselin naapuruston arvoista. Tämän naapuruston määrää suodinmaskin muoto ja koko. Yleensä maskin muoto on neliö ja sen koko on \((2k + 1) \times (2k + 1)\) pikseliä, missä \(k = 0, 1, \dots\) on tarkoitukseen soveltuva kokonaislukuvakio.
Suodinmaskin painokertoimet määräävät suotimen ytimen (eng. kernel), ja suotimen soveltamista yllä kuvatulla tavalla nimetään yleensä konvoluutioksi. Syystä joka selviää myöhemmin on luontevaa kirjoittaa prosessi matemaattiseksi kaavaksi epäilmeisellä tavalla: Olkoon annettu suotimen ydin \(H\). Ytimen \(H\) konvoluutio käsiteltävän kuvan \(F\) kanssa on lopputuloskuva \(R\). Kuvan \(R\) pikselin \((i, j)\) arvo saadaan kaavasta
\(\left[F*H\right](i,j) = R(i, j) = \sum_{u,v} H(i−u, j−v) F(u,v)\).
Tässä on tietoisesti vältetty kirjaamasta summausrajat. Sen sijaan oletetaan, että summausalue on riittävän laaja huomioimaan kaikki ytimen nollasta poikkeavat arvot. Koska usein tarkastelemme kuvia jatkuvina funktiona, on hyvä havaita, että em. konvoluutiolla on myös jatkuva vastine:
\(\left[F*H\right](x,y) = \iint_{u,v} H(x−u, y−v) F(u,v)\).
Konvoluutiosta voi muodostaa mielikuvan jossa suodinmaskia liikutellaan pikseli pikseliltä yli käsiteltävän kuvan ja maskin keskipistettä vastaava tulospikselin arvo saadaan skaalaamalla maskia vastaavat pikseliarvot maskin painoilla ja summaamalla ne yhteen. Huomaa: Tässä tapauksessa käytetään koko ajan kaikkia pikselinaapurustoja käsiteltäessä samoja painokertoimia, jolloin prosessi on lineaarinen, eli lopputulos kahden alkuperäisen kuvan summaa käsiteltäessä on sama asia kuin jos summattaisiin erikseen käsiteltyjen kuvien lopputulokset. Lisäksi vakiokertoimella skaalatun alkuperäisen kuvan käsittelyn lopputulos saadaan yhtä hyvin skaalaamalla samalla vakiolla alkuperäisestä kuvasta saatu lopputulos. Seuraavaksi esitetään lyhyt yhteenveto konvoluution ominaisuuksista, mutta niiden todistaminen jätetään kurssille Signaalinkäsittely:
Assosiatiivisuus: \(f_1*(f_2*f_3) = (f_1*f_2)*f_3\)
Kommutatiivisuus: \(f_1*f_2 = f_2*f_1\)
Distributiivisuus: \(f_1*(f_2+f_3) = f_1*f_2+f_1*f_3\)
Monilineaarisuus: \(\alpha\left(f_1*f_2\right)=\left(\alpha f_1\right)*f_2 =f_1\left(\alpha f_2\right)\)
Konjugointi (Mikäli signaalit ovat kompleksisia): \(\bar{f_1*f_2}=\bar{f_1}*\bar{f_2}\)
siirto-ominaisuus: \(T_{x,y}\left(f_1*f_2\right)= \left(T_{x,y} f_1\right)*f_2= f_1*\left(T_{x,y} f_2\right)\), missä \(\left[T_{x,y} f\right](u,v)=f(u-x,v-y)\)
Suunnattu gradientti: (Mikäli signaalit ovat jatkuvia): \(\frac{d}{d\hat{u}}(f_1*f_2)=\left(\frac{d f_1}{d\hat{u}}*f_2\right)=\left(f_1 * \frac{d f_2}{d \hat{u}}\right)\)
Konvoluutio impulssifunktiolla: \(f*\delta = f\)
Erilaisia painokerroinjoukkoja käyttäen saadaan tietenkin erilaisia kuvankäsittelyoperaatioita. Painokertoimet voivat esimerkiksi olla arvoltaan suuria lähellä suodinmaskin keskipistettä ja ne vaipuvat nopeasti nollaan etäännyttäessä keskipisteestä. Tällainen suodin voisi esimerkiksi mallittaa epäfokuksessa olevan linssijärjestelmän aiheuttamaa kuvan sumenemista. Painokertoimia ei ole rajoitettu positiivisiksi ja esimerkiksi erotusosamäärää vastaavat, suodinmaskin alueella positiivisesta negatiivisiksi muuttuvat painokertoimet mallittavat matemaattista gradienttia.
Tehtävä – Konvoluutio
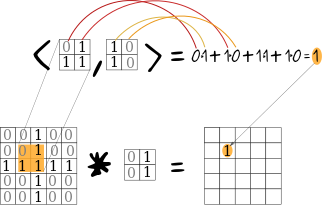
Laske kuvan 1 (2D konvoluutio ja..) puuttuvat arvot.
Olkoon \(F\) \(10\times 10\)-kokoinen kuva, missä
\(F(i,j) =\begin{cases}1,& \text{jos i=j=5}\\0,&\text{muuten}\end{cases}\)
Mitä seuraavat konvoluutiomaskit tekevät tälle kuvalle?
\(\left[1,1,1\right]\cdot\frac{1}{3}\)
\(\left[\begin{array}{ccc} 1& 1& 1\\1& 1& 1\\1& 1& 1\end{array}\right]\cdot\frac{1}{9}\)
\(\left[0,0,0,0,1\right]^T\) (Huom. Tässä tehtävässä ei tarvitse laskea mitään)
Entäpä, jos kuvassa on kaksi kirkasta pistettä?
Testaa samoja maskeja myös suurempaan kuvaan, käyttäen tietokonetta. Pitikö intuitiosi paikkaansa? (Voit käyttää graphicstools-esimerkkikoodia tai ilman graphicstoolsia toimivaa esimerkkikoodia
Esimerkki: silottaminen keskiarvoistamalla
Kuvilla on tyypillisesti se ominaisuus, että pikselin väri on samankaltainen sen naapuripikselien värin kanssa. Joskus kuvaan on sitä otettaessa tullut jostakin syystä kohinaa kuten satunnaisia “kuolleita” pikseleitä, tai pieniä nollakeskiarvoisia satunnaislukuja on jostakin teknisestä syystä summautunut pikseliarvoihin.
Tällaisissa tapauksissa on luontevaa yrittää vähentää kuvan häiriöitä korvaamalla jokaisen pikselin arvo sen naapuripikselien arvojen painotetulla keskiarvolla. Tätä prosessia kutsutaan kuvan silottamiseksi, engl. smoothing tai sumeuttamiseksi, Ensimmäinen yritelmä silotusoperaation malliksi on käyttää normaalia aritmeettista pikseliarvojen keskiarvoa yli kiinnitetyn suodinmaskialueen. Voimme esimerkiksi laskea keskiarvon kaikista \(2k + 1 \times 2k + 1\) pikselistä tarkastelupikselin ympäriltä. Käsiteltävälle kuvalle F tämä määrää lopputuloksen
\(R(i, j) = \frac{1}{(2k + 1)^2}\sum_{u=i-k}^{u=i+k}\sum_{v=j-k}^{v=j+k} F(u,v)\)
Tarkastelemalla huolellisesti summausrajat, huomataan että tämä operaatio todellakin vastaa yo. konvoluutio-operaattoria, kunhan ytimen alkioiden arvoksi asetetaan vakio \(1/(2k + 1)2\).
Tämä tapa on kuitenkin huono kuvan silottamiseen, sillä, kuten edellisessä tehtävässäkin huomasimme, esimerkiksi yksi valkoinen piste kuvan keskellä laajeneekin suuremmaksi harmaaksi neliöksi (jos et vielä tehnyt niin, varmista tämä kokeilemalla). Tämä ei juurikaan vastaa intuitiotamme siitä mitä pisteelle pitäisi tapahtua kuvan sumetessa. Jos yhden pisteen kuvamme esittää vaikkapa yhtä kirkasta tähteä mustalla yötaivaalla, niin siloitusprosessin tulisi ilmeisestikin muuttaa se valopiste neliön sijaan ympyrän muotoiseksi ja säteen suunnassa vaimenevaksi läiskäksi.
Tehtävä – Keskiarvosiloitus
- Testaa, miten vakio-arvoinen konvoluutio muuttaa yhden valkoisen pisteen kuvaa.
- Laske sopivalle kuvalle keskiarvo-siloitus eri kokoisilla maskeilla. Voit käyttää seuraavaa esimerkkiä avuksi (huomaa, että koodin kommentit löytyvät hiirellä osoittaen):

import WebTools
import CV.Filters
import CV.Matrix as M
import CV.ColourUtils
main = web "siloituskuva" "images/FourierSmall.jpg" operaatio
where
operaatio :: Image GrayScale D32 -> Image GrayScale D32
operaatio kuva = stretchHistogram ((convolve2D maski keskipiste kuva))
keskipiste :: (Int,Int)
keskipiste = (1,1)
maski = M.fromList (3,3) [-1, 1, -1
, 1, -1, 1
,-1, 1, -1]
Esimerkki: silottaminen Gaussin ytimellä
Hyvä formaali matemaattinen malli edellä mainitulle “sumealle läiskälle”on symmetrinen Gaussin ydin
\(G_\sigma(i,j) = \frac{1}{2\pi\sigma^2}\text{exp}\left(-\frac{x^2+y^2}{2\sigma^2}\right)\)
Tässä \(\sigma\) on Gaussin ytimen keskihajonta ja yksiköt ovat pikselien välisiä etäisyyksiä Vakiotermi takaa sen, että Gaussin ytimen integraali yli koko avaruuden \(\mathbb{R}^2\) on yksi. Tällä ytimellä on haluttuja ominaisuuksia:
Jos keskihajonta on hyvin pieni (pienempi kuin yksi pikseli), on silotusvaikutus hyvin vähäinen koska painokertoimet keskipistettä lukuun ottamatta ovat hyvin pieniä.
Suuremmalla keskihajonnalla lähinaapuripisteet vaikuttava lopputulokseen suuremmalla painoarvolla, jolloin keskiarvoistus johtaa lähinaapurien samankaltaistumiseen. Tämä on hyvä estimaatti pikselin arvolle, ja häiriökohina poistuu suurelta osin kuvan lievän sumeutumisen kustannuksella.
Hyvin suuri keskihajonta johtaa tilanteeseen, jossa suurin osa yksityiskohdista katoaa kohinan mukana.
Sovelluksia varten Gaussin ydin täytyy diskretoida. Tämä tapahtuu muodostamalla diskreetti ydin konstruoimalla \(2k + 1 × 2k + 1\)-taulukko \(H\), jonka arvot ovat
\(H(i, j) =\frac{1}{2\pi\sigma^2}\text{exp}\left(-\frac{(i-k-1)^2+(j-k-1)^2}{2\sigma^2}\right)\).
Keskihajonnan \(\sigma\) valinnalla on vaikutusta tarvittavaan taulukon kokoon \(k\). Jos \(\sigma\) on liian pieni, on käytännössä ainoastaan taulukon keskimmäinen alkio nollasta poikkeava. Jos \(\sigma\) puolestaan on suuri, täytyy koon \(k\) olla riittävän suuri, jotta kaikki merkittävän kokoiset painokertoimet saataisiin taulukkoon mukaan.
Tehtävä – Gaussin ydin
- Havaitse, miten konvoluutio Gaussin ytimellä muuttaa yhden valkoisen pisteen kuvaa.
- Laske herra Fourierin kuvalle (yllä) Gaussinen siloitus eri kokoisilla maskeilla ja vertaa keskiarvomaskiin. (Vinkki, voit käyttää apuna edellistä koodia. Vertaa tulostasi funktion
CV.Filters.gaussian tulokseen.)
Esimerkki: Kuvatun kohteen reunan korostaminen
Pikselikuvassa esiintyvän kuvan reuna voidaan määritellä monella eri tapaa. Yksi yleinen määritelmä on, että reuna on siellä, missä kuvassa tapahtuu äkillinen muutos. Matemaattisesti, voimme karakterisoida tätä sellaisena kuvakohtana, jolla on suuri gradientin voimakkuus. Tarkastellaan siis aluksi operaattoria, joka laskee gradientin yksikkövektorin \(\hat{u}\) suuntaan. Tälläinen operaatio voidaan johtaa lähtemällä liikkeelle gaussisesta silotuksesta. Koska gradienttioperaatio on liiankin herkkä kuvissa usein esiintyville pienille muutoksille, tämä on hyvä lähtökohta Suunnattu gradientti kuvalle ytimellä \(G\) pehmennetylle kuvalle \(f\) on
\(\left[D_{\hat{u}} (G*f)\right](x,y) = \frac{d (G*f)}{d \hat{u}} = \frac{d G}{d \hat{u}} * f\).
Koska konvoluutio ja gradientti ovat lineaarisia operaatioita ja keskenään vaihdettavissa, niin voimme erottaa gradientin laskemisoperaattorin yo. lausekkeesta: \(\frac{d G}{d \hat{u}}\), jolloin voimme käyttää jo valmiita konvoluutiofunktioita gradientin laskemiseen. Tälläisellä suotimella saisimme kyllä yhdensuuntaiset reunat kiinni, mutta suuntia lienee siinä määrin useita, että kaikkien niiden selvittäminen lieneee hankalaa. Tässä tapauksessa käy kuiten ilmi, että \(D_{\hat{u}}\) on separoituva (HT. miksi, 5 sec.), eli
\(G_{\hat{u}=(l,v)} := \frac{d G}{d \hat{u}} = l\frac{d G}{d x} +v\frac{d G}{d y} := lG_x + vG_y\),
joten voimme laskea \(x\) ja \(y\) suuntaisten operaatioiden tulokset valmiiksi ja johtaa niistä minkä tahansa suunnatun gradientin valitsemalla kertoimet \(l\) ja \(v\) sopivasti. Myöskin, voimme johtaa yksinkertaisen tuloksen gradientin voimakkuudelle \(M\) ja suunnalle \(\Theta\),
\(\left[M f\right](x,y) = \sqrt{\left[G_x * f\right](x,y)^2+\left[G_y * f\right](x,y)^2}\).
\(\left[\Theta f\right](x,y) = \text{atan2}\left(\left[G_x * f\right](x,y),\left[G_y * f\right](x,y)\right)\).
Seuraavaksi riittää laskea mitä ovat \(G_x\) ja \(G_y\):
\(G_x(x,y) = \frac{d}{dx}\frac{1}{2\pi\sigma^2}\text{exp}\left(-\frac{x^2+y^2}{2\sigma^2}\right) = -x\frac{1}{2\pi\sigma^4}\text{exp}\left(-\frac{x^2+y^2}{2\sigma^2}\right)\) ja \(G_y(x,y) = \frac{d}{dx}\frac{1}{2\pi\sigma^2}\text{exp}\left(-\frac{x^2+y^2}{2\sigma^2}\right) = -y\frac{1}{2\pi\sigma^4}\text{exp}\left(-\frac{x^2+y^2}{2\sigma^2}\right)\)
Usein gradienttioperaatioista käytetään seuraavia approksimaatioita:
\(G_x=\left[\begin{array}{ccc} 1& 0& -1\\ 2& 0& -2\\1& 0& -1\end{array}\right]\) \(G_y=\left[\begin{array}{ccc} 1& 2& 1\\ 0& 0& 0\\-1& -2& -1\end{array}\right]\)
Tehtävä
- Laske herra Fourierin kuvalla vaaka- ja pystysuuntaiset gradienttiapproksimaatiot ja gradientin magnitudi. Pystytkö erottamaan reunat kynnystämällä kuvan?
- Koska konvoluutio on niin kätevä, selvitä, kuinka monta laskutoimitusta tarvitaan, jos \(M\times N\) kokoinen kuva konvolvoidaan \(K\times K\) -kokoisella ytimellä?
Reunailmiöt diskreeteissä konvoluutioissa
Käytännön tietokonelaskennassa ei voida käyttää äärettömiä datavektoreita tai taulukoita. Tämän takia täytyy jotenkin huolehtia äärellisen (kuva)datataulukon käsittelystä taulukon reunojen lähistöllä. Reunojen lähistöllä ja reunoilla konvoluution laskennassa tarvittaisiin arvoja, joita ei ole olemassa lainkaan. Tätä ongelmaa voi lähestyä usealla vaihtoehtoisella tavalla:
Konvoluution tulosta ei lasketa lainkaan reunan lähistöllä. Tämä tarkoittaa sitä, että konvoluution tulos lasketaan vain niille tulostaulukon alkioille, joiden laskennassa tarvittava kaikki lähtödata on saatavilla. Tällä tavalla ei sorruta keinotekoiseen peukalointiin, mutta haittana on se, että tulostaulukon koko on pienempi kuin syötteen. Toistuva laskenta kutistaa lopputulosta huomattavasti.
Laajennetaan lähtödataa keinotekoisesti vakioarvoilla. Tässä tapauksessa todellisen syötedatan vaikutus vähenee merkittävästi reunan lähistöllä. Tämä voi merkittävästi vääristää tulosta, erityisesti se voi vaikuttaa merkittävästi tulosdatan derivaattaan. Etuna on tietenkin se, että tulostaulukon koko säilyy syötetaulukon kokoisena.
Laajennetaan lähtödataa muulla tavalla Lähtödata voidaan esimerkiksi mieltää tuplaperiodiseksi. Jos lähtödatataulukon koko on \(m \times m\), asetetaan laskennassa tarvittava sarake \(m + 1\) vastaamaan saraketta 1 jne. Tämä taktiikka puolestaan saattaa vaikuttaa merkittävästi tulosdatan toiseen derivaattaan reunan lähettyvillä. (Vrt. Reunailmiöt ja Fourier muunnos alempana. Naiivisti konvoluutioteoreemaa käyttäen laskettu konvoluutio käyttäytyy juuri näin.)
Tehtävä – Lorem ipsum dolor..
- Yhdistä kynnystystaitosi ja konvoluutiotietoutesi ja tee ao. lorem-ipsum kuvasta mustavalkoinen siten, että tausta on tasaisen valkoinen ja teksti musta.
Tehtävä – GraphicsTools
- Jos GraphicsTools toimii koneellasi, kokeile tehtäviä käyttäen sitä. Se on erityisen hyödyllinen erilaisten parametrien kokeilemiseen. Esimerkkejä löytyy hakemistosta graphicstoolsexamples. Voit esimerkiksi muutella Toy1.hs-tiedostoa siten, että se lataa yllä olevan lorem-ipsum-kuvan, jolloin voit kokeilla erilaisia konvoluutioita ja kynnystyksiä helposti.
- Lena.hs:n kanssa voit kokeilla värikuvan käsittelyä ja Toy2.hs:n kanssa kuvien generointia.