In this exercise, we solve the Laplace equation in two dimensions with finite differences. This may sound involved, but really amount only to a simple computation. You may want to adopt some parts of the program skeleton into your code.

Any numerical analysis text will show that iterating 

while (not converged) {y
  for (i,j)
    xnew[i][j] = (x[i+1][j] + x[i-1][j] + x[i][j+1] + x[i][j-1])/4;
  for (i,j)
    x[i][j] = xnew[i][j];
  }
will compute an approximation for the solution of Laplace's equation. There is one last detail; this replacement of xnew with the average of the values around it is applied only in the interior; the boundary values are left fixed. In practice, this means that if the mesh is n by n, then the values 
x[0][j]
x[n-1][j]
x[i][0]
x[i][n-1]
are left unchanged. Of course, these refer to the complete mesh; you'll have to figure out what to do with for the decomposed data structures (xlocal).

Because the values are replaced by averaging around them, these techniques are called relaxation methods.

We wish to compute this approximation in parallel. Write a program to apply this approximation. For convergence testing, compute 

diffnorm = 0;
for (i,j)
    diffnorm += (xnew[i][j] - x[i][j]) * (xnew[i][j] - x[i][j]);
diffnorm = sqrt(diffnorm);
You'll need to use MPI_Allreduce for this. (Why not use MPI_Reduce?) Have process zero write out the value of diffnorm and the iteration count at each iteration. When diffnorm is less that 1.0e-2, consider the iteration converged. Also, if you reach 100 iterations, exit the loop. (The solution of the test case should take a bit more than 90 iterations...) Make the program collect the computed solution onto process 0, which then writes the solution out (to standard output). You might want to write the results out in a form that can be used for display with tools like gnuplot or matlab, but this is not required. You may assume that process zero can store the entire solution. Also, assume that each process contributes exactly the same amount of data.

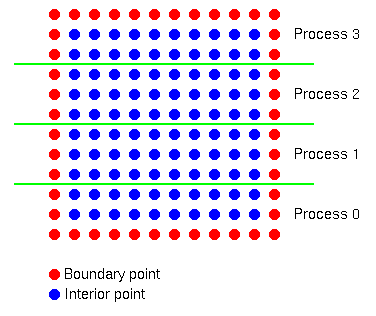
For simplicity, consider a 12 x 12 mesh on 4 processors.

The example solution uses the boundary values from the previous exercise; they are -1 on the top and bottom, and the rank of the process on the side. The initial data (the values of x that are being relaxed) are also the same; the interior points have the same value as the rank of the process. This is shown below: 

-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 
 3  3  3  3  3  3  3  3  3  3  3  3
 3  3  3  3  3  3  3  3  3  3  3  3
 2  2  2  2  2  2  2  2  2  2  2  2
 2  2  2  2  2  2  2  2  2  2  2  2
 2  2  2  2  2  2  2  2  2  2  2  2
 1  1  1  1  1  1  1  1  1  1  1  1
 1  1  1  1  1  1  1  1  1  1  1  1
 1  1  1  1  1  1  1  1  1  1  1  1
 0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1

Note that this is a very poor way to solve this numerical problem, and this method is being used only because it is very simple. Fortunately, the MPI parts of this example are very similar to those that are used in the better parallel algorithms for this problem. In particular, the use of ghost points in the parallel data structure is very similar to what is used in methods such as Conjugate Gradient or Multigrid.

You may want to use these MPI routines in your solution:
MPI_Init MPI_Finalize MPI_Send MPI_Recv MPI_Allreduce MPI_Gather MPI_Comm_size MPI_Comm_rank