Diskreetit rakenteet (ITK 015)

2. välikoe 28.11.2002 klo 12.00

1. Ilmoita permutaatiojoukkoon S₁₆ kuuluva permutaatio

erilaisten kiertojen tulona.

Pienen pienen lisäpisteen voi saada seuraavasta pulunkoloperiaatetta (Pigeonhole Principle) soveltavasta tehtävästä: Kuinka monta pulua tarvitaan, että 2¹⁰ pulunkoloa käsittävän kyyhkyslakan jostakin kolosta lentää sisään varmasti useampi kuin yksi pulu? Laskimen käyttö sallittu ;)

2. Ohessa on yksinkertainen verkko

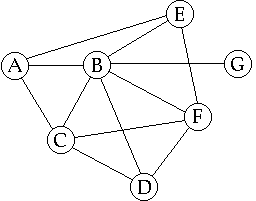
Tee verkkoa vastaava matriisi. Koska kyseessä on tasoverkko niin voit piirtää sille myös duaaliverkon. Tee se. Totea, että kumpikin verkko toteuttaa Eulerin kaavan v - e + f = 2, missä v = solmujen, e välien ja f alueiden lukumäärä. Lopuksi merkitse vielä mahdolliset sillat ja leikkaussolmut.

3. Tietokoneluokassa Asia on 10 mikroa, joista kolme on viallisia. Valitaan umpimähkään kuusi mikroa. Mikä on todennäköisyys sille, että a) mikään valituista ei ole viallinen? b) täsmälleen yksi valituista on viallinen? c) kaikki kolme viallista ovat valittujen joukossa? (Tämä on demotehtävä).

4. Luvuista 1, ...., 6 arvotaan yksi, olkoon se a. Luvuista 1, ..., a arvotaan taas yksi, olkoon se b. Ja luvuista 1, ..., b arvotaan vielä yksi. Mikä on todennäköisyys, että kolmas luku on nelonen? (Tehtävä on matematiikan laitoksen Approbatur 3:n loppukokeesta 9.1.2002, Approbatur 3:lla voi korvata tämän kurssin).