Verkkoteorian syntyhetkenä
voidaan pitää vuotta 1736, jolloin Leonhard Euler julkaisi artikkelinsa Königsbergin
siltojen ongelmasta. Königsbergin eli nykyisen Kaliningradin läpi virtasi
Pregel-joki, jonka keskellä oli saari. Tehtävänä oli kulkea jokaisen 7:n sillan
yli kerran siten että yhtäkään siltaa ei ylitetty kahdesti. Euler ratkaisi
ongelman ja ratkaisua tehdessään tuli piirtäneeksi kuvan (alla oleva verkko ja
vieressä sen matriisiesitys, jossa arvona on 1 mikäli solmuja yhdistää väli):
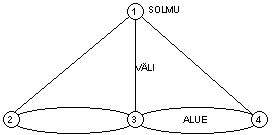

Verkko eli
graafi koostuu solmuista (node, vertex), väleistä (edge, arc, line) sekä välien
ja - mikäli kyseessä on ns. tasoverkko - solmujen erottamista alueista
(face). Eulerin kaava määrittää näiden välille suhteen: jos v, e ja
f ovat solmujen, välien ja alueiden määrät, niin v - e + f =2. Verkko voidaan
kuvata myös ja sitä kuvaava matriisi.
Tasoverkko voidaan
piirtää tavalliselle tasolle siten, että mikään sen väleistä ei leikkaa mitään
toista väliä muualla kuin solmussa. Jos verkko on tasoverkko niin sen duaalia
kutsutaan geometriseksi duaaliksi. Kun tasoverkko projisoidaan
pallopinnalle saadaan sen kanssa isomorfinen monitahokas, jonka geometrinen
duaali saadaan sijoittamalla sen sisälle toinen monitahokas, joka koskettaa kärjillään
ulomman tahokkaan tahkoja. Sekä duaaliverkon, että alkuperäisen verkon välien määrät
ovat samat, mutta alueiden ja solmujen määrät kääntäen samat. Geometrisessa
duaalissa on kärkipisteitä yhtä paljon kuin alkuperäisessä monitahokkaassa
tahkoja kun särmien määrät ovat samat.

Verkko
ja sen duaali
Verkko on yhtenäinen,
jos jokainen sen solmuista voidaan yhdistää muihin solmuihin ainakin yhdellä
välien ketjulla. Silta eli erottava väli on sellainen väli, jonka
poistaminen yhtenäisestä verkosta tekee sen epäyhtenäi-seksi. Leikkaus-
eli artikulaatiosolmu yhtenäisessä verkossa on taas solmu, jonka
poistaminen tekee verkosta epäyhtenäisen.
Tässä
esitetyt käsitteet englanniksi:
alue face
artikulaatiosolmu (leikkaussolmu) articulation
node (cutpoint, cut-node)
monitahokas polyhedron
silmukka (suljettu ketju) closed
trail (circuit)
solmu vertex,
mon. vertices (point, node, junction,
0-simplex)
tasoverkko plane
graph, planar graph
verkko graph
verkko, verkosto, painotettu verkko network
väli edge
(line,arc,edge,link,1-simplex, branch)
yhtenäinen verkko connected graph