Maailman koordinaateista ruutukoordinaatteihin
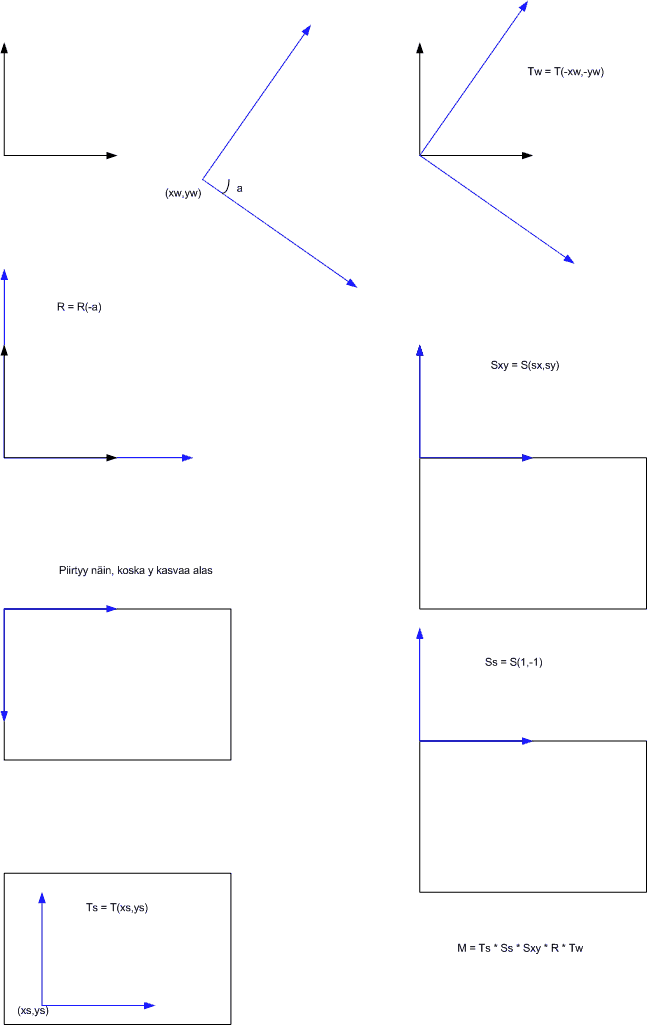
Selitykset
1) Olkoon maailma jonka "origo" on pisteessä
pw1 = (xw,yw) (world)
Maailma on kiertynyt kulmalla a
Tämä pitäisi saada ruutukoordinaatteihin.
2) Muodostetaan ensin maailman siirtomatriisi
1 0 -xw
Tw = T(-xw,-yw) = 0 1 -yw
0 0 1
3) Muodostetaan kiertomatriisi
s = sin(-a)
c = cos(-a)
c -s 0
R = R(-a) = s c 0
0 0 1
4) Lasketaan apumatriisi A
A = R * Tw
Kuva on skaalattu pisteillä p1,p2 ja p3
(joista on sekä maailman versiot pw1,pw2 ja pw3
sekä ruudun pisteet ps1,ps2 ja ps3).
Lasketaan apupisteet
pai = A * pwi ( i = 1..3 )
Lasketaan x ja y-suuntaiset skaalaussuhteet sx,sy
pisteistä pai ja psi
5) Lasketaan skaalausmatriisi
sx 0 0
Sxy = S(sx,sy) = 0 sy 0
0 0 1
6) Nyt maailman origo olisi ruudun origossa ja
maailman x-akseli ruudun x-akselin suuntainen.
Samoin maailman x ja y skaala olisi kunnossa.
Ongelmana on, että ruudulla y kasvaa alaspäin.
Siksi tarvitaan peilausmatriisi:
1 0 0
Ss = S(1,-1) = 0 -1 0
0 0 1
7) Nyt origot ovat kohdakkain ja kun otetaan isommassa
y-koordinaatissa oleva maailman piste, niin se menee
ruudun origosta ylöspäin. Tosin silloin pois ruudusta.
Tehdään vielä siirtomatriisi, jolla siirretään ps1
haluttuun kohtaan ruudulla, eli maailman origon piste
pw1 kuvautuu ruudulla pisteeseen ps1:
1 0 xs
Ts = T(xs,ys) = 0 1 ys
0 0 1
8) Lopullinen tarvittava muunnosmatriisi saadaan
M = Ts * Ss * Sxy * R * Tw

