





Tutkikaamme aikaisempia korttipakkaesimerkkejämme! Nyt tietorakenteeksi ei enää riitäkään pelkkä yksi muuttuja. Mikäli pakasta on otettu esiin pelkät padat, tarvitsisimme 13 muuttujaa. Näiden kunkin nimeäminen erikseen olisi varsin työlästä.
Tarvitsemme siis jonkin muun tietorakenteen. Mahdollisuuksia on useita: listat, jonot, pinot ja taulukot. Ohjelmoinnin alkuvaiheessa taulukot ovat tietorakenteista helpoimpia, joten keskitymme niihin aluksi.
Varataan pöydältä tilaa leveyssuunnassa 13 kortille. Varattua tilaa voimme nimittää taulukoksi tai vektoriksi. Taulukon yksi alkio on yhdelle kortille varattu paikka. Taulukon yhden alkion sisältö on se kortti, joka on siinä paikassa.
Mikäli numeroimme varatut paikat vaikkapa 0:sta alkaen vasemmalta oikealle, on meidän korteillamme osoitteet 0- 12:
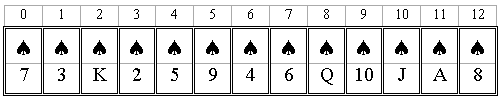
Nyt voimme käsitellä yksittäisiä kortteja aivan kuin ne olisivat yksittäisiä muuttujia. Viittaamme tiettyyn korttipaikkaan (taulukon alkioon) sen indeksillä (olkoon taulukon nimi kortit):
paikassa kortit[5] meillä on pata 9 paikassa kortit[8] meillä on pata akka
Minkälaisia algoritmeja tulee vastaan taulukoita käsiteltäessä? Esim. P 9:n siirtäminen taulukon viimeiseksi vaatisi P 4:en siirtämistä paikkaan 5. P 6:en siirtämistä paikkaan 6, PQ:n siirtämistä paikkaan 7 jne. Näin loppuun saataisiin raivatuksi paikka P9:lle.
Lajittelun ilman valtaisaa korttien siirtelyä voisimme hoitaa seuraavasti:
0. laita alku paikkaan 0 1. etsi alku paikasta lähtien pienin kortti 2. vaihda pienin ja paikassa alku oleva kortti 3. alku:=alku+1 4. mikäli alku<suurin indeksi, niin jatka 1
Sovitaan, että ässä=1. Nyt pienimmän kortin etsimisalgoritmi voisi olla seuraava:
0. Alkuarvaus: pien.paikka:=alku, tutki:=alku 1. Jos kortit[tutki] < kortit[pien.paikka] niin pien.paikka:=tutki 2. tutki:=tutki+1 3. Jos tutki<=suurin indeksi, niin jatka 1.
Voisimme vielä pöytätestata algoritmin:
|
|
pien. |
|
Kortit |
[tutki]< |
tutki< |
||||||||||||
askel |
paikka |
tutki |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
[pp] |
suur.ind |
0 |
0 |
0 |
P7 |
P3 |
PK |
P2 |
P5 |
P9 |
P4 |
P6 |
PQ |
P10 |
PJ |
PA |
P8 |
|
|
1 |
|
|
^t |
|
|
|
|
|
|
|
|
|
|
|
|
7<7 ei |
|
2&3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
juu |
1 |
1 |
|
^ |
t |
|
|
|
|
|
|
|
|
|
|
|
3<7 juu |
|
2&3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
juu |
1 |
|
|
|
^ |
t |
|
|
|
|
|
|
|
|
|
|
K<3 ei |
|
2&3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
juu |
1 |
3 |
|
|
^ |
|
t |
|
|
|
|
|
|
|
|
|
2<3 juu |
|
2&3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
juu |
1 |
|
|
|
|
|
^ |
t |
|
|
|
|
|
|
|
|
5<2 ei |
|
2&3 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
juu |
1 |
|
|
|
|
|
^ |
|
t |
|
|
|
|
|
|
|
9<2 ei |
|
2&3 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
juu |
1 |
|
|
|
|
|
^ |
|
|
t |
|
|
|
|
|
|
4<2 ei |
|
2&3 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
juu |
1 |
|
|
|
|
|
^ |
|
|
|
t |
|
|
|
|
|
6<2 ei |
|
2&3 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
juu |
1 |
|
|
|
|
|
^ |
|
|
|
|
t |
|
|
|
|
Q<2 ei |
|
2&3 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
juu |
1 |
|
|
|
|
|
^ |
|
|
|
|
|
t |
|
|
|
10<2 ei |
|
2&3 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
juu |
1 |
|
|
|
|
|
^ |
|
|
|
|
|
|
t |
|
|
J<2 ei |
|
2&3 |
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
juu |
1 |
11 |
|
|
|
|
^ |
|
|
|
|
|
|
|
t |
|
A<2 juu |
|
2&3 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
juu |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
^ |
t |
8<A ei |
|
2&3 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ei |