previous next Title Contents Index

5. Algoritmeissa tarvittavia rakenteita

Mitä tässä luvussa käsitellään?

* silmukat ja valintalauseet

* totuustaulut

* pöytätesti

* muuttujat

* taulukot

* osoittimet Vaikka jatkossa keskitymmekin oliopohjaiseen ohjelmointiin, tarvitaan yksittäisen olion metodin toteutuksessa algoritmeja. Riippumatta käytettävästä ohjelmointikielestä, tarvitaan algoritmeissa aina tiettyjä samantyyppisiä rakenteita.

Käsittelemme seuraavassa tyypilliset rakenteet nopeasti lävitse. Tarvitsisimme asioille enemmänkin aikaa, mutta otamme asiat tarkemmin esille käyttämämme ohjelmointikielen opiskelun yhteydessä. Lukijan on kuitenkin asioita tarkennettaessa syytä muistaa, ettei rakenteet ole mitenkään sidottu ohjelmointikieleen. Vaikka ne näyttäisivät kielestä täysin puuttuvankin (esim. assembler), voidaan ne kuitenkin lähes aina toteuttaa.

5.1 Ehtolauseet

Triviaaleja algoritmeja lukuunottamatta algoritminen suoritus tarvitsee ehdollisia toteutuksia: 
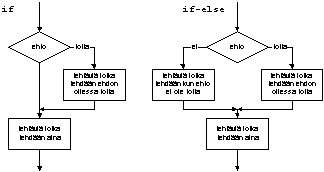
	Jos kello yli puolenyön ota taksi
	muuten mene linja- autolla
Ehtolauseita voi ehtoon tulla useampiakin ja tällöin on syytä olla tarkkana sen kanssa, mihin ehtoon mahdollinen muuten- osa liittyy: 
	Jos kello 00.00- 07.00
	  Jos sinulla on rahaa niin ota taksi
	  muuten kävele
	muuten mene linja- autolla


Kuva 5.1 Ehtolauseet

Tehtävä 5.22 Ajanlisäys

Jos sinulla on muuttujassa t tunnit ja muuttujassa m minuutit, niin kirjoita algoritmi miten lisäät n minuuttia kellonaikaan t:m.

Tehtävä 5.23 Postimaksu

Kirjoita algoritmi g- painoisen kirjeen postimaksun määräämiseksi (saat keksiä hinnaston itse).

5.2 Valintalauseet

Usein ehtoja kasaantuu niin paljon, että peräkkäiset ja sisäkkäiset ehtolauseet muodostavat varsin sekavan kokonaisuuden. Tällöin voi olla helpompi käyttää valintalausetta: 
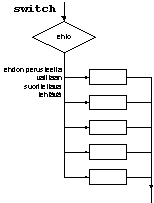
	Auto on/oli rekisterinumeron 1. kirjaimen mukaan rekisteröity seuraavassa läänissä: 
	  X     Keski- Suomen lääni
	  K     Kuopion lääni
	  M     Mikkelin lääni
	  A,U   Uudenmaan lääni


Kuva 5.2 swicth- valintalause

Tehtävä 5.24 Korvaaminen ehtolauseilla

Esitä auton rekisteröintipaikan riippuvuus rekisterin ensimmäisestä kirjaimesta sisäkkäisten ehtolauseiden avulla.

5.3 Silmukat

Hyvin usein algoritmi tarvitsee toistoa: Esimerkiksi ohjeet (vuokaavio) hiekkarannalla toimimiseksi jos nenä näyttää merelle päin:


Kuva 5.3 do- silmukka ja do-while- silmukka
Ehtolause voi olla joko silmukan alussa: mahdollisuus ettei silmukan runkoa tehdä yhtään kertaa. Ehto voi olla myös silmukan jälkeen, jolloin silmukan runko tehdään vähintään yhden kerran. Joissakin kielissä on lisäksi mahdollisuus silmukan rungon keskeltä poistuminen.

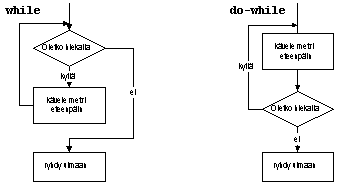
Silmukoihin liittyy aina ohjelmoinnin eräs klassisimmista vaaroista: päättymätön silmukka! Tämän takia silmukoita tulee käsitellä todella huolella. Eräs oleellinen asia on aina muistaa suorittaa silmukan rungossa jokin silmukan lopetusehtoon vaikuttava toimenpide. Mitä tapahtuu muuten?

Myös silmukan suorituskertojen lukumäärän kanssa tulee olla tarkkana. Silmukka tulee helposti suoritettua yhden kerran liikaa tai yhden kerran liian vähän.

Tehtävä 5.25 Uiminen

Mitä eroa on kahdella edellä esitetyllä "uimaan- meno" - algoritmilla? Mitä ehtoja algoritmiin voisi vielä lisätä?

Tehtävä 5.26 Ynnää luvut 1- 100

Kirjoita algoritmi lukujen 1- 100 yhteenlaskemiseksi sekä do- while- että while - silmukan avulla.

5.4 Muuttujat

Algoritmeissa tarvitaan usein muuttujia. 
	kellonaika
	rahan määrä

5.4.1 Yksinkertaiset muuttujat

Yksinkertaisessa tapauksessa muuttuja voi olla yksinkertaista tyyppiä kuten kellonaika (jos ilmaistu minuutteina), rahasumma jne.

Yksinkertainen luvun jaollisuuden testausalgoritmi voisi olla vaikkapa seuraavanlainen: 

	Jaetaan tutkittavaa lukua jakajilla 2,3,5,7...luku/2.
	Jos jokin jako menee tasan, niin ei alkuluku:
	
	0. Laita jakaja:=2, kasvatus:=1, 
	   Jos luku=2 lopeta, alkuluku
	1. Jaa luku jakajalla.  Meneekö jako tasan?
	   -  jos menee, on luku jaollinen jakajalla, lopeta 
	2. Kasvata jakajaa kasvatus arvolla (jakaja:=jakaja+kasvatus)
	3. Kasvatus:=2; (koska parillisilla ei kannata enää jakaa)
	4. Onko jakaja<luku/2?
	   -  jos on, niin jatka kohdasta 1
	   -  muuten lopeta, luku on alkuluku

Tehtävä 5.27 Vuokaavio

Piirrä jaollisuuden testausalgoritmista vuokaavio.

5.4.2 Pöytätesti

Hyvin usein algoritmi kannattaa pöytätestata. Pöytätesti alkaa kirjoittamalla sarakkeiksi kaikki algoritmissa esiintyvät muuttujat. Muuttujiksi voidaan kirjoittaa myös algoritmissa esiintyviä ehtoja. Tällainen muuttuja voi saada arvon kyllä tai ei. Pöytätestin riveiksi kirjoitetaan algoritmin eteneminen vaiheittain. Sarakkeisiin muuttujille kirjoitetaan uusia arvoja vain niiden muuttuessa.

Testataan esimerkiksi edellisen esimerkin algoritmi:

askel

Luku
Jakaja
Kasvatus
Luku/Jakaja
Jako tasan?
Jakaja<Luku/2?
Tulostus
0
25
2
1




1



12.500
ei


2

3





3


2




4





3<12.5

1



8.333
ei


2

5





3


2




4





5<12.5

1



5.000
kyllä

Jaollinen 5:llä

askel

Luku
Jakaja
Kasvatus
Luku/Jakaja
Jako tasan?
Jakaja<Luku/2?
Tulostus
0
23
2
1




1



11.500
ei


2

3





3


2




4





3<11.5

1



7.667
ei


2

5





3


2




4





5<11.5

1



4.600
ei


2

7





3


2




4





7<11.5

1



3.286
ei


2

9





3


2




4





9<11.5

1



2.556
ei


2

11





3


2




4





11<11.5

1



2.091
ei


2

13





3


2




4





13>11.5
Alkuluku
Usein pöytätesti antaa hyviä vinkkejä myös algoritmin jatkokehittelylle.

Tehtävä 5.28 Algoritmin parantaminen

Tarvitsisimmeko algoritmin kohtaa 4 lainkaan? Voitaisiinko algoritmin lopetus hoitaa muuten?

Tehtävä 5.29 Pöytätesti

Pöytätestaa edellinen algoritmi kun syöttönä on luku 121.
Pöytätestaa molemmat Ynnää luvut 1- 100 - algoritmisi versiona Ynnää luvut 1- 6.

5.4.3 Yksiulotteiset taulukot

Tutkikaamme aikaisempia korttipakkaesimerkkejämme! Nyt tietorakenteeksi ei enää riitäkään pelkkä yksi muuttuja. Mikäli pakasta on otettu esiin pelkät padat, tarvitsisimme 13 muuttujaa. Näiden kunkin nimeäminen erikseen olisi varsin työlästä.

Tarvitsemme siis jonkin muun tietorakenteen. Mahdollisuuksia on useita: listat, jonot, pinot ja taulukot. Ohjelmoinnin alkuvaiheessa taulukot ovat tietorakenteista helpoimpia, joten keskitymme niihin aluksi.

Varataan pöydältä tilaa leveyssuunnassa 13 kortille. Varattua tilaa voimme nimittää taulukoksi tai vektoriksi. Taulukon yksi alkio on yhdelle kortille varattu paikka. Taulukon yhden alkion sisältö on se kortti, joka on siinä paikassa.

Mikäli numeroimme varatut paikat vaikkapa 0:sta alkaen vasemmalta oikealle, on meidän korteillamme osoitteet 0- 12:

0

1
2
3
4
5
6
7
8
9
10
11
12













7
3
K
2
5
9
4
6
Q
10
J
A
8
Nyt voimme käsitellä yksittäisiä kortteja aivan kuin ne olisivat yksittäisiä muuttujia. Viittaamme tiettyyn korttipaikkaan (taulukon alkioon) sen indeksillä (olkoon taulukon nimi kortit): 

	paikassa kortit[5] meillä on pata 9
	paikassa kortit[8] meillä on pata akka
Minkälaisia algoritmeja tulee vastaan taulukoita käsiteltäessä? Esim 9:n siirtäminen taulukon viimeiseksi vaatisi 4:en siirtämistä paikkaan 5. 6:en siirtämistä paikkaan 6, Q:n siirtämistä paikkaan 7 jne. Näin loppuun saataisiin raivatuksi paikka 9:lle.

Lajittelun ilman valtaisaa korttien siirtelyä voisimme hoitaa seuraavasti: 

	0. laita alku paikkaan 0
	1. etsi alku paikasta lähtien pienin kortti
	2. vaihda pienin ja paikassa alku oleva kortti
	3. alku:=alku+1
	4. mikäli alku<suurin indeksi, niin jatka 1
Sovitaan, että ässä=1. Nyt pienimmän kortin etsimisalgoritmi voisi olla seuraava: 
	0.  Alkuarvaus:  pien.paikka:=alku,  tutki:=alku
	1.  Jos kortit[tutki] < kortit[pien.paikka] 
	      niin pien.paikka:=tutki
	2.  tutki:=tutki+1
	3.  Jos tutki<=suurin indeksi, niin jatka 1.
Voisimme vielä pöytätestata algoritmin: 

pien.



Kortit


[tutki]<


tutki<


askel


paikka


tutki


0


1


2


3


4


5


6


7


8


9


10


11


12


[pp]


suur.ind


0


0


0


7


3


K


2


5


9


4


6


Q


10


J


A


8




1




t














7<7 ei



2&3



1
















juu


1


1




t













3<7 juu



2&3



2
















juu


1






t












K<3 ei



2&3



3
















juu


1


3






t











2<3 juu



2&3



4
















juu


1








t










5<2 ei



2&3



5
















juu


1









t









9<2 ei



2&3



6
















juu


1










t








4<2 ei



2&3



7
















juu


1











t







6<2 ei



2&3



8
















juu


1












t






Q<2 ei



2&3



9
















juu


1













t





10<2 ei



2&3



10
















juu


1














t




J<2 ei



2&3



11
















juu


1


11














t



A<2 juu



2&3



12
















juu


1
















t


8<A ei



2&3



13
















ei

Tehtävä 5.30 Lajittelun testaus

Oletetaan, että pienimmän etsimisalgoritmi toimii. Pöytätestaa edellä esitelty lajittelualgoritmi edellisen pöytätestin mukaisella korttien järjestyksellä.
Onko tämä insertion sort? Missä on lajiteltujen kasa ja missä lajittelemattomien?

Tehtävä 5.31 Korttien poisto

Kirjoita algoritmi kuvakorttien poistamiseksi taulukosta käyttäen indeksejä.

5.4.4 Osoittimet

Edellisessä pöytätestissä merkitsimme pienen merkin niiden korttien kohdalle, joita kunakin hetkenä tutkimme. Kun tutkimme esimerkiksi paikoissa 3 ja 10 olevia kortteja (P2 ja PJ) voisimme sanoa, että muuttuja pien.paikka osoitti korttiin pata 2 ja muuttuja tutki korttiin pata jätkä. Näin ollen voisimme oikeastaan sanoa, että (indeksi)muuttujat pien.paikka ja tutki ovat osoittimia korttipakkaan. Niiden osoittamassa paikassa (indeksit 3 ja 10) on tietyt kortit (P2 ja PJ).

Lajittelualgoritmi voitaisiin lausua esimerkiksi: 

	0. levitä kortit rinnakkain pöydälle
	   osoita vasemman käden etusormella ensimmäiseen korttiin
	1. etsi vasemman käden osoittamasta kohdasta alkaen oikealle
	   pienin kortti ja osoita sitä oikean käden etusormella
	2. vaihda etusormien kohdalla olevat kortit keskenään
	3. siirrä vasemman käden etusormea yksi kortti oikealle päin
	4. 	mikäli vasen sormi vielä kortin päällä, jatka kohdasta 1.


























7

3
K
2
5
9
4
6
Q
10
J
A
8













Osoittimen ja indeksin ero on siinä, että osoittimen tapauksessa emme yleensä koskaan ole kiinnostuneita itse osoittimen arvosta (osoitteesta, siitä indeksistä missä kohdin olemme menossa), vaan osoittimen osoittaman paikan sisällöstä (sormen kohdalla olevan kortin arvo tai ei korttia). Indeksejä käsitellessämme tutkimme monesti myös itse indeksin arvoa (tutki=3 - >kortit[tutki]=P2).

Osoitin voi tarvittaessa osoittaa myös itse taulukon ulkopuolelle. Mikäli kirjoittaisimme pöydälle numeroita, voisimme osoittaa sormella yhtä hyvin pöydälle kirjoitettuja numeroita (älkää hyvät ihmiset nyt töhrätkö pöytää!) kuin pöydälle levitettyjä kortteja (taulukon alkioita).

Siis indeksit liittyvät kiinteästi taulukoihin ja osoittimet voivat liittyä mihin tahansa tietorakenteisiin alkaen yksinkertaisesta muuttujasta päätyen monimutkaisen lista- tai puurakenteen alkioon.

Tehtävä 5.32 Korttien poisto osoittimia käyttäen

Kirjoita algoritmi kuvakorttien poistamiseksi taulukosta käyttäen osoittimia.
Pöytätestaa algoritmi.

5.4.5 Moniulotteiset taulukot

Yksiulotteista taulukkoa voidaan verrata rivitaloon tai ruutupaperin yhteen riviin. Kaksiulotteinen taulukko on vastaavasti kuten kapea kerrostalo tai koko ruutupaperin yksi sivu. Tarvitsemme vastaavasti useampia osoitteita (indeksejä) osoittamaan millä rivillä ja missä sarakkeessa liikumme.

Alla on esimerkki 5x7 taulukosta (=pata, =Risti, =ruutu, =hertta):

0

1
2
3
4
5
6
0








7



A


1









K

5



2










A




3








7
2
2
9
6
3
7
4










2



J
Jos taulukon nimi on peli, niin paikassa 3,1 on kortti pata 2: 

	peli[3][1] = 2

Tehtävä 5.33 Kaksiulotteisen taulukon indeksit

Kirjoita kaikkien esimerkissä olevien korttien osoitteet em. muodossa.
Kaksiulotteista taulukkoa nimitetään usein matriisiksi.

Usein taulukoiden indeksit ilmoitetaan eri järjestyksessä kuin koordinaatiston (x,y)- koordinaatit. Tämä johtuu siitä ajattelutavasta, että taulukon rivi sinänsä voidaan kuvitella yhdeksi alkioksi (rivityypiksi) ja tällöin ilmaisu 

	peli[3]
tarkoittaa koko riviä (7, 2, 2, 9, 6, 3, 7), jonka indeksi on kolme. Mikäli tämän perään laitetaan vielä [1], niin tarkoitetaan ko. tietorakenteen alkiota jonka indeksi on yksi (2).

Tarvittaessa moniulotteiset taulukot voidaan muodostaa yksiulotteisenkin taulukon avulla. Esimerkin taulukko voitaisiin muodostaa yksiulotteisesta taulukosta siten, että yksiulotteisen taulukon 7 ensimmäistä alkiota kuvaisivat matriisin 0:ta riviä, 7 seuraavaa matriisin ensimmäistä riviä jne.

Siis mikäli yksiulotteisen taulukon nimi olisi pakka, niin voisimme käyttää samaistuksia: 

	peli[3][1] = pakka[7*3+1]
	peli[j][i] = pakka[7*j+i]
Olemme siis numeroineet kaksiulotteisen taulukon alkiot juoksevasti. Voimmehan tehdä näin myös kerrostalon huoneistoille tai teatterin istumapaikoille.

Taulukot voivat olla myös useampiulotteisia, esimerkiksi 3x4x5 taulukko: 

   0        1        2        3       4 
  +--+     +--+     +--+     +--+    +--+2 
0 | +--+   | +--+   | +--+   | +--+  | +--+1 
  +-| +--+ +-| +--+ +-| +--+ +-| +--++-| +--+0 
    +-|  |   +-|PJ|   +-|  |   +-|  |  +-|  | 
      +--+     +--+     +--+     +--+    +--+ 
  +--+     +--+     +--+     +--+     +--+     
1 | +--+   | +--+   |R5--+   | +--+   | +--+   
  +-| +--+ +-| +--+ +-| +--+ +-|HA--+ +-| +--+ 
    +-|  |   +-|  |   +-|  |   +-|  |   +-|  | 
      +--+     +--+     +--+     +--+     +--+ 
  +--+     +--+     +--+     +--+     +--+      
2 | +--+   | +--+   | +--+   | +--+   | +--+    
  +-| +--+ +-| +--+ +-| +--+ +-| +--+ +-| +--+  
    +-|  |   +-|  |   +-|  |   +-|  |   +-|  |  
      +--+     +--+     +--+     +--+     +--+  
  +--+     +--+     +--+     +--+     +--+      
3 |P7--+   | +--+   | +--+   | +--+   | +--+    
  +-| +--+ +-| +--+ +-| +--+ +-| +--+ +-| +--+  
    +-|  |   +-|  |   +-|  |   +-|  |   +-|  |  
      +--+     +--+     +--+     +--+     +--+  

	
	isopeli[0][0][1]=PJ
	isopeli[2][1][2]=R5
	isopeli[1][1][3]=HA
	isopeli[2][3][0]=P7

Tehtävä 5.34 Sijoitus 3- ulotteiseen taulukkoon

Esitä 5 muuta sijoitusta taulukkoon.

Tehtävä 5.35 3- ulotteinen taulukko 1- ulotteiseksi

Esitä kaava miten edellä oleva 3- ulotteinen taulukko voitaisiin esittää yksiulotteisella taulukolla.
Aikaisempi satunnaisen matkaajan sanastomme on oikeastaan myös kolmiulotteinen taulukko: 
	     0        1        2
	0  minä      jag       i
	1  sinä      du        you
	2  hän       han       he
Se on kaksiulotteinen taulukko sanoista. Mitä sitten yksi sana on? Se on yksiulotteinen taulukko kirjaimista! 
    0        1        2        3       4 
   +--+     +--+     +--+     +--+    +--+2      
 0 |h+--+   |ä+--+   |n+--+   | +--+  | +--+1    
   +-|s+--+ +-|i+--+ +-|n+--+ +-|ä+--++-| +--+0  
     +-|m |   +-|i |   +-|n |   +-|ä |  +-|  |   
       +--+     +--+     +--+     +--+    +--+   
   +--+     +--+     +--+     +--+    +--+2      
 1 |h+--+   |a+--+   |n+--+   | +--+  | +--+1    
   +-|d+--+ +-|u+--+ +-| +--+ +-| +--++-| +--+0  
     +-|j |   +-|a |   +-|g |   +-|  |  +-|  |   
       +--+     +--+     +--+     +--+    +--+   
   +--+     +--+     +--+     +--+    +--+2      
 2 |h+--+   |e+--+   | +--+   | +--+  | +--+1    
   +-|y+--+ +-|o+--+ +-|u+--+ +-| +--++-| +--+0  
     +-|i |   +-|  |   +-|  |   +-|  |  +-|  |   
       +--+     +--+     +--+     +--+    +--+
Siis "you" sanan indeksi on [1][2] ja sen kirjaimen "y" indeksi on [0]. Siis kaiken kaikkiaan "you"- sanan "y"- kirjaimen indeksi olisi [1][2][0].

Taulukko voitaisiin järjestää 3- ulotteiseksi myös toisinkin. Esimerkiksi yhdessä "tasossa" olisi yksi kieli jne.

Tehtävä 5.36 3- ulotteinen taulukko

Esitä edellisessä esimerkissä kaikkien kirjainten indeksit.
Millaisella yhden kirjaimen sijoituksella muuttaisit sanan "han" sanaksi "hon"?

Tehtävä 5.37 4- ulotteinen taulukko

Mitenkä tavallinen kirja voitaisiin kuvitella 3- ulotteiseksi taulukoksi?
Miten kirja voitaisiin kuvitella 4- ulotteiseksi taulukoksi?
Piirrä edellisiin perustuen esimerkki 4- ulotteisesta taulukosta ja anna muutama esimerkkisijoitus.

Osoitinmuuttuja osoittaisi myös moniulotteisessa taulukossa yhteen alkioon kerrallaan. Esimerkiksi osoittamalla "you"- sanan "y"- kirjaimeen.

Moniulotteisen ja yksiulotteisen taulukon väliset muunnokset ovat tärkeitä, koska tietokoneen muisti (1997) on lähes aina yksiulotteinen. Siis loogisesti moniulotteiset taulukot joudutaan lopulta aina toteuttamaan yksiulotteisina. Onneksi useat kielet sisältävät moniulotteiset taulukot tietotyyppinä ja kääntäjät tekevät sitten muunnoksen. Tästä huolimatta esimerkiksi C- kielessä joudutaan usein muuttamaan moniulotteisia taulukoita yksiulotteisiksi.

5.4.6 Sekarakenteet

Taulukko voi olla myös taulukko osoittimista. Esimerkiksi sanastomme tapauksessa kaikki sanat voisivat olla yhdessä "möykyssä": 
	0         1         2         3 
	0123456789012345678901234567890123
	minä jag i sinä du you hän han he
Itse sanasto voisi sitten olla taulukko osoittimia sanojen alkupaikkoihin:

0

1
2
0
00
05
09
1
11
16
19
2
23
27
31
Siis taulukon paikasta sanasto[1][0] löytyy osoitin. Tämän osoittimen arvo on tässä esimerkissä 11. Siis osoitin viittaa sanan "sinä"- alkuun. Tässä 2-ulotteinen taulukko osoittimista 1 ulotteiseen merkkitaulukkoon 
	// C++:lla
	char *sanasto[3][3];

Tehtävä 5.38 Sanojen muuttaminen

Mitä ongelmia edellä olisi, mikäli yhdenkin sanan pituutta kasvatettaisiin?
Voitaisiinko edellä käyttää samoja sanoja uudestaan ja jos niin miten?

5.5 Osoittimista ja indekseistä

Osoitinmuuttujaa voitaisiin kuvitella myös seuraavasti: Olkoon meillä osoitekirja (osoitteet) jossa on sivuja: 
sivu 0:



sivu 1:



sivu 2:


Kassinen Katto
Katto
3452



Susi Sepe
Takametsä
-



Ankka Aku
Ankkalinna
1234

Meidän osoitekirjamme on tavallaan taulukko osoittimista (tässä tapauksessa osoitteita, älä sotke termejä!). Taulukon osoitteet paikassa 1 (sivu 1) on osoite "Sepe Sudelle". Mitä tapahtuu mikäli kirjoitamme kokonaan uuden henkilön osoitteen sivulla 1 olevan osoitteen päälle (sijoitetaan uusi arvo osoitinmuuttujalle osoitteet[1])? 
sivu 1:


Batman
Gotham City
999

Mitä tapahtuu "Sepe Sudelle"? Tuskinpa sijoitus osoitekirjassamme siirtää "Sepe Sutta" yhtään mihinkään "Perämetsästä", tai tekee edes häntä murheelliseksi! Tämä on eräs tyypillinen virhekäsitys osoitinmuuttujia käytettäessä. Osoitinmuuttujaan sijoittaminen ei muuta tietenkään itse tiedon sisältöä. Mutta sijoittaminen siihen paikkaan johon osoitinmuuttuja osoittaa (esimerkissämme "Sepe Suden" asuntoon) muuttaa tietenkin myös itse tiedon sisältöä. 
	// C++:lla
	sivu[1] = uusi_osoite;    // ei vaikuta Sepe Suteen
	*sivu[1] = uusi_henkilo;  // laittaa uuden henkilön Sepen osoitteeseen
	                          // = "tähdätään osoitetta pitkin"
Vastaavasti jos meillä on indeksimuuttuja nimeltä sivu, niin sijoitus muuttujalle 
	sivu=2
ei muuta mitenkään itse sivun sisältöä. Vasta sijoitus 
	osoitteet[sivu]=
muuttaisi sivun 2 sisältöä.

5.6 Aliohjelmat

Aliohjelmat on tarkempi kuvaus tietylle asialle. Tämä kuvaus esitetään jossakin toisessa kohdassa ja sitä ei suinkaan tarvitse joka kerta lukea uudelleen.

Keittokirjassa lukee: 

	pyöritä lihapullataikinasta pyöreitä pullia
	paista pullat kauniin ruskeiksi
Miten pullat paistetaan kauniin ruskeiksi. Tämä olisi edellisen algoritmin aliohjelma. Kokenut kokki ei välitä aina (eikä edes suostuisi) joka reseptin kanssa lukea itse paistamisohjetta. Aloittelija tätä saattaisi tarvita, jottei naapuri hälyttäisi palokuntaa paikalle liian savunmuodostuksen takia. Siis toivottavasti keittokirjasta jostakin kohti löytyisi myös itse paistamisohje.

Aliohjelmille on tyypillistä, että ne saattavat suoriutua vastaavista tehtävistä eri muuttujillekin. Näitä kutsukerroista riippuvia muuttujia sanotaan parametreiksi.

Esim. lihapullan paisto- ohje saattaa semmoisenaan kelvata myös tavalliselle pullalle: 

	paista("paistettava","c")
	  Korvaa seuraavassa sana "paistettava" sillä mitä olet
	  paistamassa ja "c" sillä lämpötilalla, joka keittokirjan
	  ohjeessa ko. paistettavan kohdalla on:
	
	0. laita "paistettavat" pellille
	1. lämmitä uuni "c"- asteeseen
	2. laita pelti uuniin
	...
	9. mikäli "paistettavat" ovat mustia mene ostamaan 
	   kaupasta valmiita
	...

Tehtävä 5.39 Lihapullan paistaminen

Täydennä edellinen paistamisalgoritmi. Onko parametreja tarpeeksi?

5.7 Vaihtoehtojen tutkiminen totuustaulun avulla

Usein helpostakin tehtävästä seuraa monia eri vaihtoehtoja, joiden täydellinen hallitseminen pelkästään päässä saattaa olla ylivoimaista. Tällöin avuksi tulee totuus- ja päätöstaulut. Päätöstaulu on totuustaulun pidemmälle viety versio.

Tutkikaamme aluksi muutamaa esimerkkiä jotka eivät suoranaisesti liity ohjelmointiin, mutta joissa esiintyy täsmälleen vastaava tilanne:

5.7.1 Kaikkien vaihtoehtojen kirjaaminen

Uusien opiskelijoiden lähtötasotesti 1991 (n. 20% oli osannut vastata oikein tähän tehtävään):

Tehtävä 3.4: Seisot tienhaarassa tuntemattomassa maassa. Toinen teistä vie pääkaupunkiin. Maan asukkaat joko valehtelevat aina tai puhuvat aina totta. Toisen tien alussa seisoskelee yksi heistä. Esität hänelle kyllä vai ei - kysymyksen ja saat vastauksen. Mitä kahta seuraavista neljästä kysymyksestä olisit voinut käyttää ollaksesi varma siitä, kumpi tie vie pääkaupunkiin - riippumatta siitä valehteleeko asukas vai ei?

1.
Viekö tämä tie pääkaupunkiin?
2.
Olisitko sanonut, että tämä tie vie pääkaupunkiin, jos olisin kysynyt sinulta sitä?
3.
Onko niin, että tämä joko on tie pääkaupunkiin, tai sitten sinä puhut totta (mutta ei molemmin tavoin)?
4.
Onko totta, että tämä tie vie pääkaupunkiin ja sen lisäksi sinä puhut totta?
Erotelkaamme eri kysymykset: 1 = A Viekö pääkaupunkiin?

B Puhutko totta? (mielenkiinnon vuoksi)

2 = C Olisitko sanonut että vie jos A?

3 <- D Tie pääk. XOR puhut totta?

4 <- E Tie pääk. AND puhut totta?

Nyt voimme kirjoittaa eri vaihtoehtojen mukaan seuraavan totuustaulun (V=vastaus kun valehteleminen otetaan huomioon): 
Tie vie pää-


Puhuu


1



2



3


 



4



kaupunkiin


totta


A


B


C


D



V


E



V


E


E


K


K


E


E



K


E



K


E


K


E


K


E


K



K


E



E


K


E


E


K


K


K



E


E



K


K


K


K


K


K


E



E


K



K

Siis 2 ja 3 vastauksissa on järkevä korrelaatio siihen viekö tie pääkaupunkiin vai ei.

5.7.2 Vaihtoehtojen lukumäärä

Mistä tiedämme milloin kaikki vaihtoehdot on kirjoitettu? Mikäli systeemiin vaikuttavia asioita on n kappaletta ja kukin on kyllä/ei tyyppinen (0/1), niin vaihtoehdot on helpointa saada aikaan kirjoittamalla kaikki n- bittiset binääriluvut järjestyksessä (esimerkissämme n=2) ja suorittamalla sitten tarvittavat samaistukset (esim E=0 ja K=1). Vaihtoehtoja on tällöin 2n. 
	00   - > E  E
	01   - > E  K
	10   - > K  E
	11   - > K  K

Tehtävä 5.40 Kombinaatioiden lukumäärä

Olkoon meillä tehtävä, jossa yksi muuttuja voi saada arvot K,E,tyhjä ja toinen muuttuja arvot 5 ja 10. Kirjoita kaikki ko. muuttujien kombinaatiot.
Mikäli meillä on vaihtoehtoja n kappaletta ja kukin voi saada ki eri arvoa, niin montako eri kombinaatiota saamme aikaiseksi?

5.7.3 Useita vaihtoehtoja samalla muuttujalla

Ottakaamme toinen vastaava tehtävä:

Tehtävä 4.3: Pekka valehtelee maanantaisin, tiistaisin ja keskiviikkoisin; muina viikonpäivinä hän puhuu totta. Paavo valehtelee torstaisin, perjantaisin ja lauantaisin; muina viikonpäivinä hän puhuu totta. Eräänä päivänä Pekka sanoi: "Eilen valehtelin!" Paavo vastasi: "Niin minäkin!" Mikä viikonpäivä oli? Minä päivinä kaverukset saattaisivat sanoa ko. lausuman? Näitä päiviä on tietysti ne, jolloin joko eilen valehdeltiin ja tänään puhutaan totta TAI eilen puhuttiin totta ja tänään valehdellaan. (XOR) 

päivä


Pekka


valehteli eilen


Paavo


valehteli
eilen



sunnuntai   





k 	sanoo



maanantai   


V


	sanoo



	



tiistai     


V


k





keskiviikko 


V


k





torstai     



k 	sanoo


V


	sanoo


<==


perjantai   




V


k



lauantai    




V


k



sunnuntai   





k 	sanoo


Totuustaulun tavoitteena on siis kerätä kaikki mahdolliset vaihtoehdot ohjelmoijan silmien eteen, ja näin kaikki mahdollisuudet voidaan analysoida ja käsitellä.

Tehtävä 5.41 BAL=kyllä?

Eräällä saarella asuu luonnonkansa. Puolet kansan asukkaista aina valehtelevat ja toinen puoli puhuu aina totta. Lisäksi heidän kielensä on tuntematon. On saatu selville, että "BAL" ja "DA" tarkoittavat "kyllä" ja "ei", muttei sitä kumpiko tarkoittaa kumpaa. He ymmärtävät suomea mutta vastaavat aina omalla kielellään. Vastaasi tulee yksi saaren asukas.
a) Mitä saat selville kysymyksellä "Tarkoittaako BAL KYLLÄ"?
b) Millä kysymyksellä saat selville mikä sana on kyllä?

Tehtävä 5.42 Kuka valehtelee?

Jälleen maahan jossa asukkaat joko valehtelevat tai puhuvat aina totta. Tapaat kolme asukasta A:n, B:n ja C:n. He sanovat sinulla
A: Me kaikki kolme valehtelemme! B: Tasan yksi meistä puhuu totta!
Mitä ovat A, B ja C?
Entä jos asukkaat sanovat:
A: Me kaikki kolme valehtelemme! B: Tasan yksi meistä valehtelee!
Entä jos:
A: Minä valehtelen mutta B ei!
Entä jos:
A: B valehtelee! B: A ja C ovat samaa tyyppiä!
Vielä yksi:
A sanoo: B ja C ovat samaa tyyppiä. C:ltä kysytään: Ovatko A ja B samaa tyyppiä?
Mitä C vastaa?

5.7.4 Loogiset operaatiot

Ehtoja usein yhdistellään loogisten operaatioiden avulla: 
	Mikäli kello 7- 20 ja et halua ulkoilla
	-  mene bussilla
	...
	Mikäli sinulla on rahaa tai saat kimpan
	-  ota taksi
Yksittäinen ehto antaa tulokseksi tosi (T=true) tai epätosi (F=false). Ehtojen tulosta voidaan usein myös kuvata 1 tai 0. Ehtojen yhdistämistä loogisilla operaatioilla kuvaa seuraava totuustaulu (myös C++:n loogiset operaattorit merkitty): 







ja




tai



ehd. tai



ei











AND




OR




XOR




NOT





p




q


 


p


&&


q


p


||


q


p


^


q



!


p


 ^ toimii jos p ja q boolean


F



0


F



0


F



0


F



0


F



0


T



1



F



0


T



1


F



0


T



1


T



1


T



1



T



1


F



0


F



0


T



1


T



1


F



0



T



1


T



1


T



1


T



1


F



0


F



0


Huomattakoon edellä, että AND operaatio toimii kuten kertolasku ja OR operaatio kuten yhteenlasku (mikäli määritellään 1+1=1). Siis loogisia operaattoreita voidaan käyttää kuten normaaleja algebrallisia operaattoreita ja niillä operoiminen vastaa tavallista algebraa. Loogisten operaatioiden algebraa nimitetään Boolen - algebraksi.

Ehtojen sieventämisessä käytettäviä kaavoja voidaan todistaa oikeaksi totuustaulujen avulla. Todistetaan esimerkiksi de Morganin kaava (vrt. joukko- oppi, 1=true, 0=false): 

	NOT (p AND q) = (NOT p) OR (NOT q)
	
	Jaetaan ensin väittämä pienempiin osiin:
	NOT   e1      =   e2    OR   e3

 
e1


e2


e3





p


q


p AND q


NOT p


NOT q


NOT e1


e2 OR e3



0


0


0


1


1


1


1



0


1


0


1


0


1


1



1


0


0


0


1


1


1



1


1


1


0


0


0


0


Koska kaksi viimeistä saraketta ovat samat ja kaikki muuttujien p ja q arvot on käsitelty, on laki todistettu!

Tehtävä 5.43 de Morganin kaava

Todista oikeaksi myös toinen de Morganin kaava:
NOT (p OR q) = (NOT p) AND (NOT q)

Tehtävä 5.44 Osittelulaki

Yhteenlaskun ja kertolaskun välillähän pätee osittelulaki:
p * (q + r) = (p * q) + (p * r)
Samaistamalla * <=> AND ja + <=> OR todetaan loogisille operaatioillekin osittelulaki:
p AND (q OR r) = (p AND q) OR (p AND r)
Todista oikeaksi toinen osittelulaki (toimiiko vast. yhteenlaskulla ja kertolaskulla):
p OR (q AND r) = (p OR q) AND (p OR r) 



e1


e2


e3





p


q


r


q AND r


p OR q


p OR r


p OR e1


e2 AND e3



0


0


0








0


0


1








0


1


0








0


1


1








1


0


0








1


0


1








1


1


0








1


1


1







Huomaa, että totuustauluun tulee nyt 8 riviä (koska kolme muuttujaa)!

Tehtävä 5.45 Ehtojen sieventäminen

Käytä de Morganin kaavoja tai osittelulakia seuraavien ehtojen sieventämiseen:
a)
ei ole totta että hinta alle 5 mk ja paino yli 10 kg
b)
NOT (kello<=7 OR rahaa>50 mk)
c)
((hinta < 5) tai (rahaa>10)) ja ((hinta < 5) tai (kello>9))

5.8 Muistele tätä

Mikäli edellä esitetyt asiat tuntuvat ymmärrettäviltä, niin ohjelmoinnissa ei tule olemaan mitään vaikeuksia. Jos vastaavat asiat tuntuvat vaikeilta ohjelmoinnin kohdalla, kannattaa palata takaisin tähän lukuun ja yrittää samaistaa asioita ohjelmointikieleen.

Taulukoiden samaistaminen ruutupaperiin, korttipakkaan tai muuhun tuttuun asiaan auttaa asian käsittelyä. Osoitinmuuttuja on yksinkertaisesti jokin (vaikkapa sormi) joka osoittaa johonkin (vaikkapa yhteen kirjaimeen).

Silmukat ja ehtolauseet ovat hyvin luonnollisia asioita.

Aliohjelmat ovat vain tietyn asian tarkempi kuvaus. Tarvittaessa tiettyä asiaa ei ongelmaa tarvitse heti ratkaista, vaan voidaan määritellä aliohjelma, joka hoitaa homman ja kirjoitetaan itse aliohjelman määrittely joskus myöhemmin.

Tehtävä 5.46 Merkkijonot

C- kielessä merkkijonot tullaan esittämään taulukoina kirjaimista. Merkkijonon loppu ilmaistaan kirjaimella NUL. Siis esimerkiksi Kissa olisi seuraavan näköinen 
0


1


2


3


4


5



K


i


s


s


a


NUL


Kirjoita seuraavat algoritmit. Erityisesti kirjoita ensin algoritmin sanallinen versio
1.
Välilyöntien poistaminen jonon alusta.
2.
Välilyöntien poistaminen jonon lopusta.
3.
Ylimääräisten (2 tai useampia) välilyöntien poistaminen jonosta.
4.
Kaikkien ylimääräisten (alku- ,loppu- ja monikertaiset) välilyöntien poistaminen.
5.
Jonon muuttaminen siten, että kunkin sanan 1. kirjain on iso kirjain.
6.
Tietyn merkin esiintymien laskeminen jonosta.
7.
Esiintyykö merkkijono toisessa merkkijonossa (kissatarha, sata - > esiintyy; kissatarha, satu - > ei esiinny).

Tehtävä 5.47 Päivämäärät

Kirjoita seuraavat algoritmit:
1.
Onko vuosi karkausvuosi vai ei. (Huom! 1900 ei, 2000 on)
2.
Montako karkausvuotta on kahden vuosiluvun välillä.
3.
Jos 1.1 vuonna 1 oli maanantai, niin mikä viikonpäivä on 1.1 vuonna x? (Oletetaan että kalenteri olisi ollut aina samanlainen kuin nytkin. Vihje! Tutki almanakkaa peräkkäisiltä vuosilta.)
4.
Onko päivämäärä pp.kk.vv oikeata muotoa?

previous next Title Contents Index