Raportti käsittelee matematiikan verkko-opetusprojektin toimintaa ajalla 1.4.-31.12.2003. Projektin yleisiä tavoitteita olivat matematiikan verkko-opetuksen tukeminen, joka käsittää teknisen tulen verkko-opetusmateriaalin tuottajille sekä yhteistyön muiden lähialan projektien ja laitosten kanssa. Lisäksi projektissa tutkittiin olemassaolevia matemaattisia ohjelmistoja ja oppimisympäristöjä sekä niiden hyödyntämismahdollisuuksia. Myös uusia ohjelmistoja kehitettiin.
Projektin tilaajina ovat Jyväskylän yliopiston avoin yliopisto, virtuaaliyliopisto sekä matematiikan ja tilastotieteen laitos. Projektin vetäjänä toimi Mikko Saarimäki. Tero Tilus toimi projektissa suunnittelijana vuonna 2002 ja Miika Nurminen 1.4.-31.12.2003. Antti Viholainen laati Java Sketchpad -havainnollistuksia kesällä 2002 ja Satu pelkonen LiveMath -tehtäviä kesällä 2003. Avoimen yliopiston opettajista projektissa ovat olleet mukana myös Kaija Häkkinen, Päivi Kujansuu, Janne Kauhanen ja Janika Konnu. Yhteistyötä tehtiin myös peda.net-projektin ja TKK:n MatTa-projektin kanssa.
Luvussa 2 käsitellään matematiikan julkaisuprosesseja. Luvussa 3 käydään läpi projektin aikana tutkitut ja kehitetyt ohjelmistot. Luvussa 4 esitellään muiden organisaatioiden kokoamia matematiikan opetusmateriaalikokoelmia. Luku 5 on yhteenveto. Kaikki raportissa mainitut WWW-linkit on koottu erilliseen TopicTree-ohjelmistolla toteutettuun linkkipuuhun.
Yksinkertaisin ratkaisu matemaattisen tekstin julkaisuun on kirjoittaa materiaali tavallisen tekstin tapaan (esim. HTML-sivuna) ja upottaa kaavat tekstin mukaan kuvina. Ratkaisu on tyydyttävä, jos kaavoja ei ole tekstissä kovin paljoa ja teksti on tarkoitettu vain luettavaksi. Jos kaavoja on enemmän, tekstin tuottamiseen kannattaa käyttää paremmin matematiikkaa tukevia ohjelmistoja, kuten LATEX-ladontaohjelmaa. Jos teksti kuuluu johonkin tehtäväkokonaisuuteen tai sen tulisi sisältää interaktiivisia elementtejä, julkaisu mutkistuu entisestään.
Varsinaisen teksti- ja kaavamateriaalin lisäksi myös kuvat ja muut havainnollistukset ovat olennaisia, erityisesti opetusmateriaaleissa. Ohjelmia on saatavilla runsaasti, mutta ne ovat usein erikoistuneita tai huonosti siirretäviä. Käyttömahdollisuudet vaihtelevat rasterikuvista pieniin virtuaalimaailmoihin.
Matematiikka koostuu olennaisilta osiltaan käsitteistä ja niiden suhteiden analysoinnista. Matemaattisen kirjallisuuden perinteiset määritelmä-lause-todistus -ketjut ovat täsmällisiä, mutta voivat jättää erityisesti kokemattomalle lukijalle hämäräksi taustalla olevan käsiterakenteen. Siksi matemaattisessa tekstissä tulisi käyttää nykyistä enemmän käsitekarttoja ja kaavioita käsitteiden havainnollistukseen. Käsitekartat soveltuvat sekä opetusmateriaaliin että opiskelijoiden omaan käyttöön tiettyä asiakokonaisuutta hahmoteltaessa. Ohjelmia on runsaasti saatavilla, joskin niiden laatu vaihtelee suuresti.
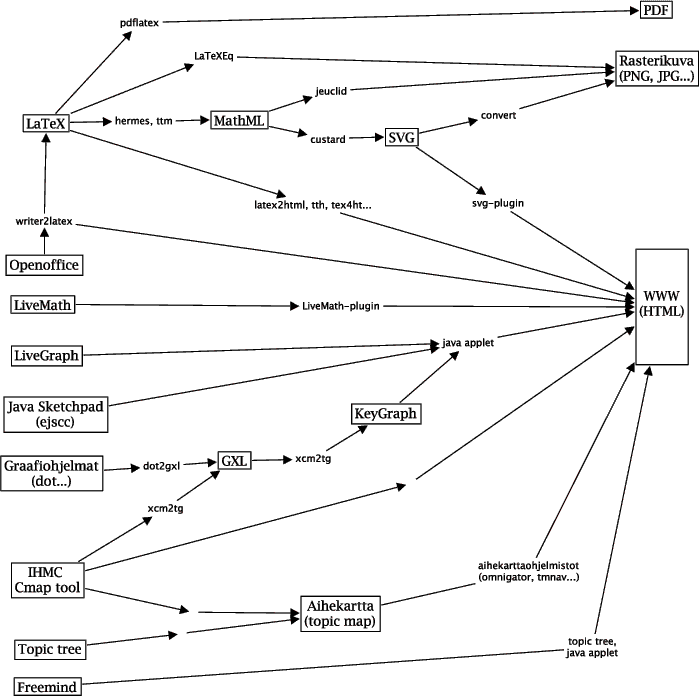
Kuvassa 2.1 on esitetty eräitä matemaattisen materiaalin julkaisuprosesseja tärkeimmillä projektin aikana tutkituilla ohjelmistoilla. Ohjelmistojen teknisiä ominaisuuksia käsitellään tarkemmin luvussa 3.

LATEX on korkealaatuisten tieteellisten ja matemaattisten dokumenttien toteuttamiseen parhaiten sopiva ladontajärjestelmä, jonka useimmat toteutukset ovat ilmaisia. Varsinaisesti LATEXon makropakkaus, joka hyödyntää TEX-ladontaohjelmaa. LATEX-dokumentti on puhdasta tekstiä, joka sisältää merkintäkomentoja sivun loogisesta rakenteesta ja muotoilusta hieman HTML-dokumenttien tapaan. Lähestymistapa poikkeaa nykyisistä tekstinkäsittelyohjelmista, joissa dokumentin ulkoasu on nähtävissä suoraan editoitaessa. Tämä ''ohjelmointikielimäisyys'' vaatii hieman totuttelua tekstinkäsittelyohjelmiin tottuneille, mutta soveltuu hyvin erityisesti materiaalille, joka sisältää runsaasti matemaattisia kaavoja. LATEXin kielen oppimiskynnyksen ylittämisen jälkeen LATEXin käyttö voi olla jopa tekstinkäsittelyohjelmia tehokkaampaa. [17]
LATEX ei sellaisenaan sovellu WWW-julkaisemiseen, koska ohjelma ei tuota HTML-kieltä. Tällä hetkellä LATEX-dokumentteja on käytännöllisintä julkaista WWW:ssä PS- tai PDF-muodossa (LATEX -järjestelmä sisältää ohjelmat kumpaakin formaattia varten). Formaatit ovat hyvin siirrettäviä: niille on saatavissa esikatseluohjelmia eri käyttöjärjestelmille. Ongelmana on, että niiden luku tietokoneruudulla on työlästä, jolloin erityisesti laajat dokumentit on usein tulostettava. PDF-tiedostoihin on mahdollista lisätä hyperlinkkejä, mutta niiden käyttö on kömpelöä HTML-dokumentteihin verrattuna. LATEX-dokumentteja pystyy näyttämään suoraan WWW-selaimessa myös Integren Techexplorer1-plug-inin avulla, joka on yksityiskäytössä ilmainen.
LATEX-dokumentteja on mahdollista muuttaa HTML-muotoon muunnosohjelmien avulla. Ohjelmia on tarjolla useita ja niitä on kuvattu tarkemmin luvussa 3.2. Valitettavasti mikään niistä ei toimi kaikissa tilanteissa tyydyttävästi. Perusongelmana on LATEX-järjestelmän laajennettavuus: järjestelmälle on saatavilla valtavasti laajennuspaketteja, jotka sisältävät uusia muotoilukomentoja. Kaikkien näiden tulkinta WWW-ympäristön kannalta järkevästi on ongelmallista. Yksinkertaisten dokumenttien muuttaminen HTML-muotoon kuitenkin onnistuu. Muunnosohjelmien perussideana on yleensä vektorikuvien muuttaminen rasterikuviksi ja matemaattisten kaavojen muuttaminen edelleen kuviksi tai (jos mahdollista) HTML-muotoon. [9]
Jos tuotettavassa tekstissä ei ole suurta määrää matemaattisia kaavoja eikä LATEXia ole käytettävissä, helpoin ratkaisu on käyttää jotain tekstinkäsittelyohjelmaa. Esim. Microsoft Word ja OpenOffice sisältävät kaavaeditorit, joilla varsinkin yksinkertaisten kaavojen syöttäminen onnistuu suoraan ohjelman sisällä. Nykyiset tekstinkäsittelyohjelmat sisältävät myös HTML-ulostulon, jolloin tekstin saa myös WWW:hen. Kaavat muunnetaan yleensä kuviksi (OpenOfficelle on saatavilla myös MathML-muunnosohjelma, katso luku 3.2.2).
Jos tekstinkäsittelyohjelmien kaavaeditorien ominaisuudet eivät riitä, on saatavilla myös erillisiä kaavaeditoriohjelmia, kuten Design Sciencen kaupallinen MathType2, joka on integroitavissa Microsoft Wordiin ja tuottaa tarvittaessa myös MathML:aa tai LaTeX-koodia. Kevennetty versio MathTypesta on saman yhtiön tuottama ilmainen TEXaide, jossa kaavoja voi editoida Microsoft Wordin kaavaeditorin tyylisellä ohjelmalla ja tuloksen voi kopioida TEX-koodina.
SVG [6] (Scalable Vector Graphics) ja MathML [3] (Mathematical Markup Language) ovat W3C:n määrittelemiä XML-pohjaisia kieliä, esimmäinen vektorigrafiikan ja jälkimmäinen matematiikan esittämiseen WWW:ssä. Molemmilla on laajat linkkisivustot W3C:n sivuilla3. Kieliä voidaan käyttää yhdessä HTML:n kanssa ja ihannetapauksessa teksti ja dokumentin rakenne kuvattaisiin HTML-kielellä, matemaattiset kaavat MathML:llä ja kuvat SVG:llä. Valitettavasti WWW-selaimet eivät vielä tällä hetkellä tue kunnolla kumpaakaan kieltä. Molemmille on saatavilla runsaasti plug-ineja ja muunnosohjelmia, mutta vain Mozilla-selaimeen on saatavilla osittain toimiva natiivitoteutus4. Yksinkertaisilla kaavoilla Mozillan MathML-toteutus toimii raportin kirjoitushetkellä (Mozillan versio 1.5) jo varsin hyvin.
SVG:tä ja MathML:aa voidaan käyttää varsinaisen julkaisuformaatin ohella myös väliformaatteina. Esimerkiksi LATEX-dokumentti on mahdollista muuntaa MathML:ksi ja edelleen SVG:ksi. Jotkut matemaattiset ohjelmistot, kuten Mathematica, osaavat lukea MathML-kieltä, jolloin sillä voidaan siirtää tietoa ohjelmistojen välillä. MathML:n tuottaminen onnistuu helpoiten muunnosohjelmien tai kaavaeditorien avulla - käsin kirjoitettavaksi MathML ei sovellu runsaasti elementtejä sisältävän rakenteensa takia. WWW-selaimissa SVG yleistynee ennen MathML:aa, joten kaavojen esittäminen SVG-muodossa voi olla perusteltua (tällöin kaavojen ulkoasu on vektorigrafiikan ansiosta rasterikuvia laadukkaampi).
WWW-ympäristössä MathML-kieltä käytetään pääasiassa matemaattisten kaavojen ulkoasun esittämiseen. Siirrettäessä tietoa matemaattisten ohjelmistojen välillä oleellisempaa on kuitenkin kaavan merkitys. MathML tukee molempia lähestymistapoja sisältäen erilliset presentaatio- ja semantiikkamoduulit. Esimerkiksi [11] kaava (a+b)(c+d) voidaan kuvata ulkoasutilassa seuraavasti:
<mrow> <mrow><mo>(</mo><mi>a</mi> <mo>+</mo> <mi>b</mi><mo>)</mo></mrow> <mo>⁢</mo> <mrow><mo>(</mo><mi>c</mi> <mo>+</mo> <mi>d</mi><mo>)</mo></mrow> </mrow>Toisaalta sama kaava merkitään semantiikkatilassa seuraavasti:
<apply> <times/> <apply><plus/><ci>a</ci> <ci>b</ci></apply> <apply><plus/><ci>c</ci> <ci>d</ci></apply> </apply>MathML:n käyttäminen esim. symbolialgebraohjelmistoissa syöteformaattina vaatii nimenomaan semantiikkatilan käyttöä, koska kaavan ulkoasun kuvaaminen ei kuvaa yksikäsitteisesti kaavan merkitystä. Kun jokin ohjelmisto väittää olevansa MathML-yhteensopiva, on syytä tutkia, onko kyse presentaatio- vai sisältötason yhteensopivuudesta (esim. MathML-plug-init ja Mozillan MathML-tuki keskittyvät lähinnä ulkoasuun).
Semantiikkatilasta huolimatta MathML on ensisijaisesti keskittynyt ulkoasun kuvaamiseen. Sen semantiikkatilan tukema matemaattisten symbolien määrä on melko rajallinen. Vaihtoehto semanttiselle MathML:lle on pelkästään kaavojen semantiikan kuvaamiseen keskittyvä, myös XML-pohjainen OpenMath5-kieli. Se on suunniteltu erityisesti matemaattisten kaavojen semantiikan esittämiseen. Kaavojen kaikki elementit määritellään formaalisti kielessä itsessään olevien laajennusmekanismien avulla. Standardien matemaattisten olioiden esitykset on julkaistu WWW:ssä ns. sisältöhakemistoina (Content Dictionary), jota käyttämällä eri OpenMathia tukevat sovellukset voivat sopia yhteisistä käsitteistä. [16]
Laajin ja yleisin matemaattisiin merkistöihin kantaa ottava standardi on Unicode, jonka tarkoituksena on koodata kaikki ihmiskunnan käyttämät merkit. Unicode-merkistö on tällä hetkellä 32-bittinen. Pelkästään matemaattisia merkkejä ja symboleja on tällä hetkellä noin 2000 [1]. Unicode soveltuu luonnostaan WWW-ympäristöön, koska HTML- ja XML-dokumentit voidaan määritellä sillä koodatuksi (Esim. useilla WWW-sivuilla käytetty UTF-8 -koodaus on Unicoden esitystapa). Matemaattisen tekstin esittäminen pelkkää Unicodea käyttäen ei tällä hetkellä ole vielä käytännöllistä muotoiluongelmien takia, mutta standardoitu merkistö helpottaa matematiikan esittämistä esim. MathML-dokumentissa. Edellytyksenä on tietysti Unicodea (tai ainakin sen matematiikkaosaa) tukeva fontti.
Web-ympäristö soveltuu erinomaisesti havainnollistuksiin, animaatioihin ja muuhun interaktiiviseen sisältöön, jonka toteuttaminen perinteisillä välineillä ei ole välttämättä mahdollista. Erilaisia visualisointiohjelmia ja interaktiivisia laskimia onkin runsaasti tarjolla. Yksinkertaisia ja helposti käyttöönotettavia vaihtoehtoja ovat Javapohjaiset 3D-visualisointiohjelmat, kuten LiveGraphics 3D tai JavaView (katso luku 3.1.3), joiden interaktiivisuus rajoittuu lähinnä 3D-mallien pyörittelyyn. Kehittyneemmissä ohjelmissa ruudulle voi lisätä ohjauspainikkeita tai tekstikenttiä, joiden perusteella käyttäjä pääsee muokkaamaan havainnollistusta tai laskukaavoja. Tällaisia ohjelmia ovat esimerkiksi LiveMath (katso luku 3.1.1) tai Java Sketchpad (katso luku 3.1.2). Järeämpi ratkaisu on Mathematica-ohjelman WWW-laajennus webMathematica, jossa laskenta suoritetaan palvelimella. Suurin osa interaktiivisista matematiikkaohjelmistoista on kaupallisia.
Design Science -yhtiön Math on the Web -raportissa [14] tutkittiin interaktiivisten ohjelmistojen osuutta tämän hetken www-sivuista käyttäen Google-hakukoneen suosituimpia tuloksia tietyillä matematiikkaan liittyvillä hakusanoilla. Testatuista sivuista suurimmassa osassa matemaattinen teksti esitettiin joko HTML-kielellä yhdistettynä rasterikuvisiin kaavoihin tai PDF-tiedostoina. Erityisesti MathML:n käyttö oli vähäistä. Interaktiivista sisältöä oli vain noin 20% sivuista ja niistäkin suurimmassa osassa interaktiivisuus oli toteutettu JavaScript-kielellä tai sekalaisilla Java-sovelmilla. Maple- tai Mathematica-ohjelmilla tuotettua sisältöä oli jonkin verran, mutta varsinaisilla interaktiiviseen matematiikkaan suunnitelluilla ohjelmistoilla (esim. LiveMath tai Design Sciencen oma WebEQ) tuotettuja sivuja ei juuri ollut. Raportissa pääteltiin, että suurin osa interaktiivisesta matematiikasta on suljetuilla sivustoilla, joille hakukoneet eivät pääse. Toinen vaihtoehto on, että interaktiivista matematiikkaa varten ei vielä(kään) ole yleiskäyttöisiä ja laajalle levinneitä ratkaisuja.
Käsitteellinen mallinnus on jonkin sovellusalueen käsitteiden ja niiden välisten suhteiden selvittämistä. Mallinnukseen on olemassa lukuisia eri kieliä, formalismeja ja notaatioita, joiden täsmällisyys vaihtelee suuresti. Käsitteelliseen mallinnukseen suunniteltuja kieliä ovat esimerkiksi olio-ohjelmoinnissa käytetty UML (Unified Modeling Language) tai tietokantasuunnittelussa käytettävät ER-kaaviot. Semanttiset verkot ja käsitegraafit ovat tekoälytutkimuksessa käytettyjä formalismeja, pedagogiikassa puhutaan yleensä käsitekartoista tai mind mapeista. Nimestä tai sovellusalueesta riippumatta käsitteelliset mallit ovat nimettyjä ja tyypitettyjä graafeja, joissa solmut vastaavat käsitteitä tai olioita, kaaret niiden välisiä suhteita.
Käsitteellistä mallinnusta hyödyntäviä ohjelmia ja järjestelmiä on runsaasti saatavilla. Hyvä yleiskatsaus ja laaja linkkikokoelma on esimerkiksi J.P.van Schien Concept mapping -artikkeli [21]. Lisäksi John Redmood ylläpitää kommentoitua linkkikokoelmaa6 Windows-käyttöjärjestelmälle saatavista käsitekartta- ja hahmotelmaohjelmista.
Käsitekarttojen avulla on mahdollista kuvata laajoja asiakokonaisuuksia kompaktissa muodossa. Carnot & al. [5] olivat vertailleet opiskelijoiden hakunopeutta ja oppimiskykyä kun tiedot oli organisoitu joko käsitekartoiksi tai tavanomaisiksi WWW-sivuiksi. Tutkimuksen perusteella käsitekartat vaikuttivat positiivisesti molempiin tutkimuskohteisiin. Lisäksi monet opiskelijat pitivät käsitekarttoihin perustuvaa käyttöliittymää WWW-sivuja miellyttävämpänä oppismistuloksista riippumatta.
Käsitekarttoja ei tällä hetkellä juuri käytetä matematiikassa opetusvälineinä eikä matematiikkaan liittyviä esimerkkejä löytynyt myöskään WWW:ssä olevista käsitekartoista. Siitä huolimatta käsitekartoista voisi olla suuri apu matematiikan opiskelussa: matematiikkahan koostuu nimenomaan täsmällisesti määritellyistä käsitteistä, jotka pohjautuvat alkeellisemmille käsitteille, joita käytetään todistettaessa uusien käsitteiden ominaisuuksia. Matemaattinen teksti koostuu suurimmaksi osaksi määritelmä-lause-todistus -ketjuista, joiden seuraaminen edellyttää usein hyppimistä sivulta toiselle edellisiin tuloksiin - joskus teorian alkeellisimpiin määritelmiin asti. Käsitekartan avulla opiskelija voi yhdellä silmäyksellä nähdä teorian keskeiset käsitteet ja tulokset, jotka auttavat myös todistuksen seuraamista (vaikka niitä ei sellaisenaan voi todistamiseen käyttääkään).
Saatavilla olevien käsitekarttaohjelmien laatu, ominaisuudet ja hinta vaihtelevat laidasta laitaan. Suurin ohjelmien ongelma on, että ne eivät yleensä ole yhteensopivia keskenään. Uudemmissa ohjelmissa formaatit ovat yleensä XML-pohjaisia, mikä helpottaa muunnosohjelmien tekoa, mutta yleisesti hyväksyttyä ja useimmissa käsitekarttaohjelmissa käytettyä standardia ei ole. Eräs kandidaatti graafien rakenteen talletukseen on XML-pohjainen GXL-kieli7 (Graph eXchange Language), joka on käytössä muutamissa graafinpiirto-ohjelmissa. Kieli on suunniteltu tiedonsiirtoformaatiksi graafipohjaisten työkalujen välille [23]. Se kuvaa ainoastaan graafien rakenteen lisättynä tyypeillä ja attribuuttitiedolla. Ulkoasun (esim. fontit, solmujen paikat) esittämiseen GXL ei sovellu, vaan se täytyy koodata jollain erillisellä kielellä, esim SVG:tä käyttäen. Saatavilla on myös joitakin automaattisia muotoilijoita, kuten ATT:n DOT-ohjelma (katso luku 3.3.4).
Matemaattisen tekstin kannalta keskeinen ongelma on, että nykyiset käsitekarttaohjelmat tukevat lähinnä puhdasta tekstiä - TEX-tyylinen monimutkaisten kaavojen merkintä ei onnistu suoraan. Tilanne helpottuu hieman, jos käsitekarttaan saa yhdistettyä kuvia tai HTML-koodia. Tällöin matemaattinen osa tekstistä voidaan merkitä nykyisten WWW-sivujen tapaan. Laajoissa teksteissä tämä ei kuitenkaan ole käytännöllistä. Käsitekarttaohjelmista tarkempaan tarkasteluun valittiin IHMC:n Concept Map Tools -ohjelma, josta tarkempi kuvaus on luvussa 3.3.1.
Puut ovat syklittömiä erikoistapauksia graafeista. Hierarkkisen rakenteen ansiosta niiden käsittely onnistuu yleisiä graafeja tehokkaammilla välineillä. Myös monet käsitekartat voidaan kuvata täysin puumaisesti. Tyypitetyissä graafeissa on lisäksi usein eroteltavissa puumaisia osarakenteita (esim. oliopohjaisen ohjelmiston luokkien perintäsuhteet muodostavat yleensä puun mutta luokkien yleiset liitossuhteet muodostavat graafin).
Käsitekarttaohjelmien tapaan myös puurakenteiden luontia ja käsittelyä varten on saatavilla runsaasti ohjelmia, joita kutsutaan myös hahmotteluohjelmiksi (outliners). Ne on suunniteltu lähinnä muistilistojen, esitysten rakenteen suunnittelun ja yleensäkin ideoinnin avuksi korvaamaan perinteisiä paperille tehtäviä ''ranskalaisia viivoja''. Hahmotteluohjelmien ominaisuuksia on otettu mukaan myös tekstinkäsittelyohjelmiin. Projektin aikana kehitetty TopicTree-ohjelma (katso luku 3.5.8) on yksinkertainen hahmotelmaohjelma, vaikka onkin varsinaisesti suunniteltu linkkikokoelmien hallintaan. Varsinaisista hahmotteluohjelmista käsitellään tarkemmin Freemind-ohjelmaa (katso luku 3.3.2).
Sovellettaessa hahmotelmaohjelmia matematiikkaan ohjelmissa on samoja ongelmia kuin käsitekarttaohjelmissa: tiedon perusyksiköt ovat puhdasta tekstiä, mahdollisesti hyperlinkeillä tai kuvilla tehostettuna. Lisäksi eri ohjelmat ovat yleensä keskenään yhteensopimattomia. Puurakenteista tekstimuotoista tietoa varten on esitetty väliformaatiksi XML-pohjaista OPML-kieltä (Outline Processing Markup Language), joka on lähtöisin web-päiväkirjajärjestelmästä Radio UserLand [22].
Skillen [19] selvittää hahmotelmaohjelmien käyttöä perusopetuksessa. Ryhmätyönä tehdyt hahmotelmat olivat toisaalta auttaneet asioiden ymmärtämistä, toisaalta oppilaat olivat oppineet tietojen jäsennysmalleja, jotka ovat sovellettavissa varsinaisen opetustilanteen ulkopuolella. Tietokoneella tehdyt hahmotelmat ovat käsintehtyihin verrattuna ylläpidettävämpiä ja niiden julkaisu verkossa on helppoa (kuvien ja kaavojen esittäminen on tosin tällä hetkellä suoraviivaisempaa paperilla).
Aihekartat (Topic Maps) on ISO:n standardoima8 kieli WWW:n resurssien kuvaamiseen. Niillä voidaan kuvata käsitteellisiä rakenteita ja liittää niitä tietolähteisiin. Aihekartat ovat toisaalta yleistys kirjojen hakemistoille (hakemisto on aihelista, esiintyminä sivunumerot), toisaalta ne voidaan tulkita aiheista ja assosiaatioista muodostettuina semanttisina verkkoina. Aihekarttoja voidaan visualisoida graafeiksi, mutta ensisijaisesti kyseessä on malli tietämyksen rakenteen esittämiseen hieman tietokantojen relaatiomallin tapaan. Aihekarttoja voidaan esittää SGML- tai XML-pohjaisella kielellä. [18]
Aihekarttojen peruskäsitteet ovat aiheet (topic), ilmentymät (occurrence) ja assosiaatiot. Käsitekarttojen kannalta aiheet vastaavat verkon solmuja, assosiaatiot linkkejä ja ilmentymät ovat solmulle kuuluvia resursseja. Aiheet voivat olla tyypitettyjä ja tyypit muodostavat oman hierarkiansa. Assosiaatiot ovat aina kaksisuuntaisia (suuntien päät ovat assosiaation rooleja, esim. työsuhde-assosiaation roolit ovat työnantaja ja työntekijä) ja tiettyyn assosiaatioon voi kuulua periaatteessa rajattomasti rooleja. Eri lähteissä olevia aihekarttoja voidaan myös yhdistää, jos niillä on yhteiseksi tunnistettuja aiheita.
Aihekartat soveltuvat hakuteostyylisiin sovelluksiin tai laajojen linkkikokoelmien hallintaan. Jotkut yritykset markkinoivat aihekarttoja ratkaisuna kaikkiin tietämyksenhallinnan ongelmiin, mutta yleiskäyttöisiä, toimivia sovelluksia on vielä vähän saatavilla. Aihekarttoja pidetään myös kilpailijana W3C:n kehittämille semanttisen webin tekniikoille, kuten RDF- ja OWL-kielille [15]. Parhaiten aihekartat soveltuvat kuitenkin alkuperäisessä tarkoituksessaan: rajoitetun sovellusalueen käsitteiden havainnollisena hakemistona. Hyvä esimerkki aihekarttapohjaisesta palvelusta on Steven Wilden ylläpitämä WWW Online Glossary9, WWW-tekniikoiden, standardien ja muiden ''hämärien kirjailyhenteiden'' sanakirja.
Aihekarttojen laajamittaisessa hyödyntämisessä on tällä hetkellä vielä useita hankaluuksia, joista tärkeimpänä on edullisten sovelluskehysten ja komponenttien puute. Esimerkiksi rakennettaessa aihekarttapohjaista WWW-portaalia suuri osa työstä - erityisesti käyttöliittymän osalta - on koodattava manuaalisesti. Käyttöliittymien osalta valmiita aihekarttaselaimia on muutamia, esimerkiksi Ontopia-yhtiön tuottama Omnigator-selain10. Valmiit selaimet ovat kuitenkin liian yleiskäyttöisiä ja teknisiä loppukäyttäjää ajatellen ja soveltuvat lähinnä kehitysvaiheen prototyypeiksi (Tilannetta voi verrata tietokantojen selaamiseen suoraan relaatiotaulutasolta). Sovelluskehittäjien kannalta tilanne kuitenkin helpottunee lähitulevaisuudessa. Lupaava projekti on esimerkiksi TM4J11, jonka tavoitteena on kehittää avoimen lähdekoodin komponetteja aihekarttojen käsittelyyn ja (web-)sovelluskehitykseen.
Aihearttojen käyttöönoton ongelmat tulevat hyvin esille Carlstedtin ja Nordborgin Pro Gradu -tutkielmassa [4], jonka yhteydessä he olivat toteuttaneet aihekarttapohjaisen järjestelmän laajan dokumenttikokoelman hallintaan. Tietomallin luonti, erityisesti assosiaatioiden mallinnus tuotti ongelmia. Monet sovellusalueen suhteet olivat luonnostaan yksisuuntaisia, jolloin assosiaatioroolien määritys kaksisuuntaisesti heikensi aihekartan ymmärrettävyyttä. Lisäksi assosiaatioihin olisi kaivattu tyypin lisäksi myös attribuutteja. Dokumenttien luokittelussa aiheiden ilmentymiksi oli aluksi yritetty käyttää automaattista kategorisointiohjelmaa, mutta luokittelu ei ollut onnistunut tyydyttävästi.
Luvussa käsitellään projektin kannalta keskeisimpiä ohjelmistoja. Lista ei missään tapauksessa ole täydellinen eikä välttämättä edes edustava, koska ohjelmien kirjo on erittäin laaja. Kaavaeditorien ja raskaiden matematiikkaohjelmien käsittely on jätetty tarkoituksella pois ja keskitytty opetusmateriaalin kannalta keskeisiin interaktiivisiin ohjelmiin sekä julkaisuprosessissa tarvittaviin muunnosohjelmiin. Käsitekarttaohjelmat eivät varsinaisesti ole matemaattisia ohjelmia, mutta niitä on käytetty ja testattu projektin aikana ja raportin kirjoittaja uskoo, että niillä voisi olla käyttöä matematiikan(kin) opetuksessa (katso luku 2.5). Työryhmäohjelmistot ovat tarpeellisia kaikessa verkko-opetuksessa, matematiikan opetus mukaanlukien.
Tässä käsiteltyjen ohjelmistojen lisäksi eräitä mielenkiintoisia ohjelmia on koottu verkko-opetusprojektin linkkipuuhun. Myös Tero Tiluksen muistiossa [20] on arvioitu matemaattisia ohjelmia ja oppimisympäristöjä. WWW:ssä on saatavilla runsaasti linkkikokoelmia matemaattisista ohjelmistoista, esimerkiksi MatTa-projektin sivuilla 12 on laajahko kommentoitu lista ladonta- ja julkaisujärjestemistä ja matemaattisista ohjelmistoista.
Käsitellyistä ohjelmista Java Sketchpadilla ja LiveMathilla on tehty havainnollistuksia matematiikan approbaturkursseja varten. Livegraphics ja Javaview ovat 3D-visualisointiohjelmia, jotka ovat yhteensopivia Mathematica-ohjelmiston kanssa. WebEQ on DesignScience-yhtiön kaupallinen ohjelma interaktiivista matematiikkaa varten.
LiveMath13 on Theorist Interactive -yhtiön kehittämä ohjelmapaketti interaktiivisen matematiikan tuottamiseen ja web-julkaisuun. Kaavapohjat kirjoitetaan kaupallisella LiveMath Maker -ohjelmalla, jonka käyttöliittymä perustuu ikoneihin. Ohjelman tekijät kehuvat mahdollisuutta tuottaa kaavoja ilman mitään ohjelmointia, mutta ohjelmoijan näkökulmasta kaavojen kirjoittaminen graafisten painikkeiden avulla ilman mahdollisuutta automatisoida tuotantoa tuntuu vaivalloiselta. Kaavoja kirjoitettaessa virheitä sattuu helposti ja niiden korjaaminen saattaa vaatia mutkikkaita toimintasarjoja. Teksti tallennetaan LiveMathin omaan formaattiin, jonka muokkaaminen muilla ohjelmilla (tai edes ohjelmallisesti) ei onnistu helposti.
LiveMathin kaavat näytetään WWW-ympäristössä LiveMathin omalla plug-inilla. Ohjelmiston paras ominaisuus on kaavojen interaktiivinen ratkaiseminen ja muokkaaminen: tekstiin voi jättää avoimia kenttiä, joihin arvoja sijoittamalla kaavaa seuraavat yhtälöt muuttuvat välittömästi. Muokkaus toimii hyvin yksittäisillä numeerisilla arvoilla, mutta kaavojen rakenteen muuttaminen on rajoitetumpaa. On mahdollista tehdä kaavapohja, jossa näytölle lasketaan käyttäjän melko vapaasti antaman funktion mukainen kuvaaja, mutta esilaskettujen kaavojen rakennetta ei voi muuttaa.
Ohjelmaa testatessa havaittiin, että plug-inin tekstikenttien muokkaaminen on hankalaa kokemattomalle käyttäjälle. Odottamattomassa muodossa kirjoitettu vastaus tai parametri johtaa virheilmoitukseen. Tällöin kuvaajaikkuna tai esilasketut kaavat voivat seota, pahimmillaan koko sivu on ladattava uudestaan. Toinen ongelma oli LiveMath Makerin ohjelmoitavuuden puute. Monipuolisten kaavapohjien tekeminen edellyttäisi esimerkiksi ehtolauseen tai silmukan kaltaisia käsitteitä. Laajoja kuvaajia selattaessa liukulukujen laskentatarkkuus aiheutti epäsäännöllisyyksiä kuvaajaan.
Pieni käyttöliittymäongelma oli myösplug-in -ikkunan koon staattinen määräytyminen. Kaavapohjiin voi sisällyttää piilotettuja elementtejä, jotka eivät näy WWW-sivua ladatessa, mutta jotka voi ottaa esille laskemisen edetessä. Plug-in -ikkunan koko määräytyy kuitenkin alussa näkyvän kaavapohjan mukaan, jolloin kaavoja saattaa kadota näkyvistä. Ikkunaa ei voi vierittää. Ratkaisuna kokeiltiin plug-in-ikkunan koon dynaamista muuttamista php-skriptillä. LiveMath-keskusteluryhmässä ehdotettiin myös ylimääräisten kommenttien lisäämistä kaavapohjan loppuun.
Puutteistaan huolimatta LiveMath on lupaava ohjelma, jonka dynaaminen lähestymistapa kaavojen esittämiseen on ainutlaatuinen muihin WWW:ssä oleviin matematiikkaohjelmiin verrattuna. LiveMath Maker on saatavissa Windowsille, Linuxille, Macintoshille ja Solarikselle. Plug-inista on versiot Netscapelle ja Internet Explorerille. Satu pelkosen laatimat LiveMath-kaavapohjat ovat selattavissa matematiikan approbaturin WWW-sivujen alla14.
Java Sketchpad15 on Geometer's Sketchpad -geometriaohjelman laajennus, joka mahdollistaa interaktiivisten kuvaajien sijoittamisen Java-sovelmaan. Kuvaajia voidaan parametrisoida sovelman sisällä vierityspalkkien kaltaisilla ohjaimilla. Sovelmat ovat erittäin helppokäyttöisiä ja suhteellisen havainnollisia, joskaan niille ei ole ohjelman kapasiteetista johtuen mahdollista laittaa kovin suurta määrää objekteja.
Java Sketchpadin pahin puute sen komentokielen hankaluus. Sovelman rakenne muodostetaan antamalla sille parametreina joukko muotoilukomentoja, jotka muodostavat oman ohjelmansa. Muotoilukomennot ovat hankalia käyttää mm. pakollisten, absoluuttisten rivinumeroiden takia. Tero Tilus suunnitteli kesällä 2002 ejscc-kääntäjän havainnollistusten luonnin helpottamiseksi (katso luku 3.5.2). Antti Viholaisen laatimat havainnollistukset ovat selattavissa matematiikan yleisopintojen WWW-sivujen alla16.
LiveGraphics3D17 on Martin Krausin kehittämä kevyt, ilmainen 3D-visualisointiohjelma, joka toimii Java-sovelmana. Ohjelma lukee Mathematica-ohjelmiston dokumentteja ja piirtää niiden perusteella 3D-kuvaajan, jota käyttäjä voi pyörittää hiirellä. Syötetiedostot ovat tekstiä, joten Mathematica ei ole välttämätön näkymien luontiin. Käyttäjän puolella erityisohjelmia ei tarvita, kunhan selain näyttää Java 1.1 -sovelmia.
Ohjelman erikoisuus on mahdollisuus lisätä 3D-näkymiin erityisiä toimintopisteitä, joista vetämällä näkymää voi muuttaa (tyypillisesti toimintopisteessä kiinni olevat viivat liikkuvat pisteen mukana). Sovelman 3D-piirto -ominaisuudet ovat hyvää perustasoa ja ruudunpäivitys toimii nopeasti. Ohjelma soveltuu lähinnä yksinkertaisiin havainnollistuksiin.
JavaView18 on piirto-ominaisuuksiltaan LiveGraphicsia kehittyneempi (mm. läpinäkyvät polygonit), mutta muuten ominaisuuksiltaan hyvin lähellä LiveGraphicsia oleva visualisointiohjelma. Myös JavaView on toteutettu Java-sovelmana, vaatimuksena Java 1.2. JavaViewin 3D-objektit tallennetaan ohjelman omalla formaatilla, mutta myös Mathematica- ja Maple-ohjelmien objekteja on mahdollista käyttää. Ohjelma tuntuu käytössä hieman LiveGraphicsia hitaammalta. Opetusmateriaalin tuottamisen kannalta hyödyllinen ominaisuus on 3D-näkymän talletusmahdollisuus mm. EPS-formaattiin.
WebEQ19 on Design Science -yhtiön kaupallinen ohjelma interaktiivisen matematiikan esittämiseen WWW:ssä. Se kuuluu samaan tuoteperheeseen MathTypen ja TeXaide-ohjelmien kanssa. Matematiikkaa tuotetaan sivuille Microsoft Wordin kaavaeditorin tyylisellä ohjelmalla, sisäisenä esitysformaattina on MathML. Ohjelma lukee myös TEX-koodia. WWW-sivuilla kaavat ja muut komponentit esitetään Java 1.4.1 -sovelmilla, joissa kaavojen fonttikokoa voi skaalata.
Interaktiivista matematiikkaa WebEQ tukee joukolla valmiskomponentteja, kuten kuvaajan piirtäjä, web-kaavaeditori ja laskijakomponentti, jolla voi esim. harjoitustehtävässä verrata opiskelijan kirjoittaman kaavan arvoa vastauksen arvoon. LiveMathista poiketen interaktiivisuus saadaan aikaan ohjelmoimalla, Java-sovelmien toimintaa voi ohjata JavaScript-koodilla.
WebEQ vaikuttaa raskaalta ratkaisulta melko rajoitettuun ongelmajoukkoon. Ohjelmiston web-sivuilla mainostettu ''interaktiivinen matematiikka'' tuntuu melko staattiselta verrattuna LiveMathin lennossa vaihtuviin yhtälöihin. Positiivisena ja helppokäyttöisenä yksityiskohtana mainittakoon kaavaeditorisovelma, joka mahdollistaa todella helpon (Microsoft Word-tyylisen, LATEX-käyttäjille turhan tehoton) kaavojen kirjoituksen suoraan Web-sivulla. Sovelmien ohjaus JavaScriptilla mahdollistaa potentiaalisesti monipuolisten sivustojen rakentamisen, mutta vaatii ohjelmointia. Saatavilla on myös lisäkomponentteja esim. animaatioita varten. MathML:n käyttö helpottaa yhteistoimintaa muiden matematiikkaohjelmien kanssa.
Tero Tilus [20] toteaa, että järjestelmä on turhan raskas pelkkään kaavojen näyttämiseen. Lisäksi kaavojen laatu on TEX-ladontaan verrattuna heikohko. Järjestelmästä saa MathML-koodia ulos, mutta muunnosohjelmia MathML:stä TEXiin ei juuri löydy. Kevyempi vaihtoehto kaavojen generointiin verkossa on LATEXEq-skripti (katso luku 3.5.4).
WebMathematica20 on kaupallisen Mathematica-ohjelmiston matematiikkapaketti. Sen tekniikka perustuu Java-servleteihin. WebMathematica-sovelluksia käytetään yleensä HTML-lomakkeilla, laskenta tapahtuu palvelimella ja servlet generoi uuden WWW-sivun, jossa on laskennan tulos ja mahdolliset havainnollistukset omassa sovelmassaan. WebMathematicaan kuuluu web-pohjaisten matematiikkasovellusten kehitystä tukeva ohjelmointikirjasto.
WebMathematican etuna on, että valmiiden web-sovellusten käyttäjät voivat hyödyntää periaatteessa koko Mathematica-ohjelman kapasiteettia ilman, että sitä tarvitsee asentaa käyttäjän koneelle. Toisaalta matematiikkasovellusten teko vaatii ohjelmointia ja HTML-lomakkeisiin perustuvan käyttöliittymän mahdollisuudet ovat rajalliset. WebMathematican sivuilla on runsaasti esimerkkisovelluksia, joista tunnetuin lienee The Integrator21, WWW-ympäristössä toimiva symbolinen integrointisovellus.
Muunnosohjelmia on verkosta saatavilla runsaasti. Erityisesti LATEX ® HTML -muunnokseen on suunniteltu useita ohjelmia, joista mikään ei toimi kaikissa tilanteissa oikein (katso luku 2.1). Erityisesti ongelmia on vektorikuvien käsittelyn ja harvinaisten laajennuspakettien kanssa.
Convert22 on monipuolinen ilmaisohjelma kuvatiedostojen muuntamiseen ja käsittelyyn komentoriviltä. Ohjelma on asennettu valmiiksi moniin Linux-levityksiin ja on saatavissa myös Windowsille. Ohjelma osaa käsitellä suurta määrää eri kuvaformaatteja mukaanlukien vektoriformaatit EPS ja PDF (vaativat GhostScriptin tai vastaavan), joita ohjelma tosin käsittelee rasterikuvien tapaan.
Convert-ohjelmalla voi kätevästi tehdä komentorivillä rutiininomaisia kuvankäsittelyoperaatioita, jotka ovat usein tarpeellisia myös matemaattisista kaavoista generoiduille kuville. Hyödyllisiä toimintoja ovat esimerkiksi reunojen poistaminen crop-valitsimella tai läpinäkyvän värin määrittäminen transparent-valitsimella. Kuvankäsittely tehostuu huomattavasti yhdistämällä nämä esim. kaikki hakemiston kuvatiedostot kerralla läpi käyvään skriptiin.
Writer2LATEXja Writer2xhtml23 ovat Henrik Justin kirjoittamia avoimen lähdekoodin muunnosohjelmia OpenOfficen dokumenttien muuntamiseen LATEX-koodiksi tai XHTML:ksi. Ohjelmia voi käyttää joko komentoriviltä, OpenOfficesta tai minkä tahansa Java-ohjelman kutsuna. Ohjelma parantaa matemaattista tekstiä sisältävien julkaisujen laatua LATEXin parempien ladontaominaisuuksien ansiosta. HTML-muunnin tuottaa validia XHTML-koodia. Kaavat muunnettaan MathML:ksi HTML:n sisällä, mikä rajoittaa tekstin näyttöä useimmilla nykyselaimilla, mutta tukee W3C:n suosituksia. Rasteri- tai vektorikuvien osalta muunnoksia ei tehdä, joten kuvat näkyvät jos selain (tai LATEX) ymmärtää niitä.
Writer2LATEX-ohjelmaa ei testattu projektin aikana laajamittaisesti, mutta sen käyttöä voi suositella OpenOfficella työskenteleville henkilöille, jos tekstin kirjoittaminen suoraan LATEXilla ei ole mahdollista. Tulevia WWW-selaimia ajatellen myös XHTML+MathML -tuki on hyödyllinen.
TeX4ht24 on E. M. Gurarin kehittämä ilmainen komentorivipohjainen muunnosjärjestelmä, joka hyödyntää muunnoksessa suoraan LATEXin tuottamaa DVI-tiedostoa. Tällöin järjestelmää voidaan periaatteessa käyttää millä tahansa LATEX-paketeilla. HTML-ulostulon lisäksi ohjelma osaa generoida MathML:ää ja saatavilla on myös muunnosohjelmat OpenOfficelle ja Microsoft Wordille (!) sekä XML-pohjaisille dokumenttiformaateille DocBookille ja TEI:lle. Kaavat ja EPS-kuvat käännetään ulostuloformaatista riippuen rasterikuviksi. Ohjelma on saatavilla Windowsille ja eri Unix-järjestelmille.
TeX4ht on käytössä mm. TKK:n matematiikan laitoksella. Sen hyviä puolia ovat mm. konfiguroitavuus kaavojen muuntamisen suhteen ja hypertekstilinkkien sisällyttäminen dokumentteihin. Ongelmia aiheutuu siitä, että kaikille LATEXin makroille ei välttämättä ole tukea. Lisäksi kaavojen esittäminen fonteilla voi johtaa epäselviin lausekkeisiin esimerkiksi tapauksissa, missä ylä- tai alaindekseillä on indeksejä [9]. Muunnosohjelman käytössä saattaa tulla ongelmia, jos alkuperäinen tiedosto käyttää bittikarttakuvia tai PDF-vektorikuvia ja se on käännetty pdfLATEX-komennolla suoraan PDF-muotoon. TeX4ht ymmärtää vain EPS-muotoisia kuvia, joten alkuperäiseen tiedostoon liittyviä kuvia voi joutua muuntamaan.
TTH25 ja TTM ovat I. Hutchinsonin kehittämiä muunnosohjelmia. TTH:n perusversio on saatavilla ilmaiseksi ei-kaupalliseen käyttöön Windowsille ja Linuxille. TTH ei käytä LATEXia lainkaan muunnoksen apuna ja on täten huomattavasti kevyempi ohjelma esim. TeX4ht-sovellukseen verrattuna. Toisaalta ohjelma on myös ominaisuuksiltaan rajallisempi. LATEXin laajennettavuudesta johtuen ohjelma ei tue kuin pientä osajoukkoa kaikista saatavilla olevista laajennuspaketeista. Matemaattisia kaavoja ei käännetä kuviksi, vaan ne esitetään fonteilla niin pitkälle kuin mahdollista (se, mitä ei pystytä esittämään, jätetään TEX-muotoon). PS-kuvat muunnetaan valinnaisesti rasterikuviksi tai sitten ne merkitään HTML-dokumentteihin linkkeinä.
TTH on TeX4ht:ta nopeampi ohjelma ja yksinkertaisempi asentaa. Se soveltuu dokumentteihin, joissa ei ole monimutkaisia kaavoja ja jotka eivät käytä harvinaisempia LATEX-paketteja. Jos alkuperäisen dokumentin tuottamisessa on käytetty pdfLATEX-ohjelmaa, on huomattavaa, että TTH ei osaa tehdä muunnoksia PDF-kuvatiedostoille.
Custard26 on SchemaSoftin kehittämä Java-pohjainen muunnosohjelma. Perusversio on saatavilla ilmaiseksi. Ohjelma sisältää runsaasti esimerkkejä ja tekee muutenkin siistiä jälkeä, mutta sen käyttö laajojen, runsaasti kaavoja sisältävien dokumenttien kanssa on vaivalloista. Kaavat täytyy muuntaa yksi kerrallaan. SVG-tuki kuitenkin yleistynee selaimissa ennen MathML-tukea, joten tämän kaltaisille muunnosohjelmille lienee käyttöä lähitulevaisuudessa.
Batik27 on Apachen XML -projektin kehittämä, Java-pohjainen SVG-työkalupaketti. Muiden Apache-ohjelmistojen tapaan ohjelmiston lähdekoodit ovat vapaasti saatavilla. Työkaluja käytetään komentoriviltä. Batik-paketti sisältää mm. työkaluja SVG-grafiikan tuottamiseen ohjelmallisesti, grafiikan näyttämiseen Java-ohjelmissa ja muuntamiseen edelleen rasterimuotoon tämän hetken selaimia varten.
Työkalupaketti on monipuolinen ja suositeltava, jos tarkoituksena on käsitellä SVG-grafiikkaa osana laajempaa Java-sovellusta. Mielenkiintoinen (mutta ominaisuuksiltaan vielä melko rajoittunut) työkalu on myös gxl2svg-ohjelma, joka muuntaa GXL-graafeja SVG-muotoon muotoillen samalla graafin automaattisesti.
IHMC Concept Map tool soveltuu hyvin käsitekarttojen tuottamiseen, TouchGraph soveltuu paremmin jo valmiiden graafien katseluun. Projektin aikana kehitetty Xcm2kg (katso luku 3.5.6) yhdistää ohjelmat melko luonnollisesti. Graphviz on työkalupaketti graafien muotoiluun ja muunnoksiin.
IHMC Concept Map tool28 on Institute of Human and Machine Cognition -organisaation kehittämä Javapohjainen käsitekartta- ja työryhmäohjelmisto. Se on saatavilla toistaiseksi ilmaiseksi WWW:stä, joskaan lähdekoodia ei ole jaossa. Java-käyttöliittymästä johtuen ohjelma on melko raskas käyttää, mutta jos konetehoa riittää (PC-koneilla käytännössä vähintään 500MHz, 120MB RAM), ohjelma on erittäin helppokäyttöinen ja käsitekarttojen luonti onnistuu sulavasti. Syksyllä 2003 ohjelmasta julkaistiin 3. versio.
Ohjelman hyviä puolia ovat mm. seuraavat:
Testattaessa havaittuja huonoja puolia ovat seuraavat:
Pienistä puutteista huolimatta ohjelma soveltuu hyvin nopeasti luotavien ja kooltaan rajoitettujen käsitekarttojen luontiin. Erillisen palvelimen avulla ohjelma toimii myös ryhmätyöohjelmistona, jossa käsitekarttoja voi jakaa ja jopa editoida samanaikaisesti. Xcm2kg-muunnosohjelma (katso luku 3.5.6) laajentaa ohjelmalla luotujen käsitekarttojen selausmahdollisuuksia.
FreeMind29 on Java-pohjainen vapaaohjelma (GPL) puumaisten käsitekarttojen luontiin. Ohjelma on huomattavasti IHMC Concept Map toolsia kevyempi, mutta puurakenteen tuottamaa rajoitusta lukuunottamatta suhteellisen monipuolinen ohjelma. Ohjelman hyviä puolia ovat mm. seuraavat:
Ohjelmassa ei ole pahempia puutteita sen käyttötarkoitus huomioiden. Ohjelman oma HTML-tulostulo on hieman kömpelöä käyttää, mutta XML-formaatista johtuen omien XSLT-muunnosten tekeminen on melko suoraviivaista. Projektissa toteutettiin XSLT-muunnostiedosto, joka luo TopicTree-tyylisen HTML-puun, jossa linkkejä voi selata näppäimistöllä (katso luku 3.5.8).
TouchGraph30 on Alex Shapiron kehittämä, avoimen lähdekoodin projektina julkaistu käyttöliittymäkomponentti. Se perustuu Java 1.3 -sovelluksessa tai sovelmassa ajettavaan graafinäkymään, jossa graafin solmuja voidaan liikutella hiirellä vapaasti. Tyypillisesti käyttäjä ei näe koko graafia, vaan tietyn solmun ympärille keskittyneen näkymän. Graafiavaruudessa voi navigoida valitsemalla hiirellä uuden näkyvän solmun, jolloin järjestelmä hakee uuden solmun naapurit ja muotoilee näkymän uudelleen.
TouchGraph Linkbrowser on käyttöliittymäkomponentista edelleen kehitetty sovellus, jossa jokaiseen verkon solmuun liittyy URL-linkki. Tällöin linkkiselainta voidaan käyttää WWW-sivuston navigoinnin apuna (esim. kehyspohjainen sivusto, jossa toisessa kehyksessä on TouchGraph-sovelma ja toisessa varsinaiset kohdesivut). Lisäksi jokaiselle solmulle voidaan voidaan määritellä vinkkilaatikko (tooltip), joka näkyy käyttäjän pitäessä hiirtä solmun päällä. Vinkkilaatikossa voidaan näyttää HTML-koodia, erityisesti siis kuvia ja URL-linkkejä.
TouchGraph-käyttöliittymä soveltuu laajojenkin graafien visualisointiin, koska koko graafia ei tarvitse näyttää kerralla. Toisaalta käyttäjä saattaa eksyä hyvin laajaan solmujoukkoon eikä solmujen liikuttelu sinänsä auta asiaa. Graafin rakenteen ja solmujen ulkoasun (värit, muodot) huolellinen suunnittelu toki helpottaa navigointia. Verkon kaaret ovat suunnattuja, mutta niille ei voi antaa mitään lisämääreitä (esim. kaaren tyyppi). TouchGraphin formaatti on XML-pohjainen ja on siis periaatteessa käsin kirjoitettavissa, mutta käytännössä tiedostojen luonti kannattaa jättää koneelle. LinkBrowserin mukana tulee minimaalinen editori, jolla solmuja voi lisätä ja muokata suoraan TouchGraph-sovelmassa, mutta sen käytettävyys on heikohko käsitekarttaohjelmiin verrattuna.
KeyGraph (katso luku 3.5.7) on projektin aikana toteutettu paranneltu versio LinkBrowserista. Se parantaa TouchGraphin käyttöliittymää entisestään ja laajentaa tiedostoformaattia hieman. Xcm2kg (katso luku 3.5.6) on muunnosohjelma, jolla graafeja voi tuottaa automaattisesti IHMC Concept Map tool -käsitekarttaohjelman tiedostoista (katso luku 3.3.1). TouchGraph vaikuttaa erittäin lupaavalta käyttöliittymäratkaisulta, joskin se tarvitsisi hakutoimintoa tai selaushistoriaa laajojen graafien navigointia helpottamaan.
Graphviz31 on AT&T-yhtiön kehittämä avoimen lähdekoodin työkalupaketti graafien muotoiluun ja esittämiseen eri formaateilla. Paketti on saatavilla Windows- ja Unix-järjestelmille ja toimii komentoriviltä. Graphviz-paketin merkittävimmät ohjelmat ovat dot- neato- ja twopi-muotoilijat, jotka generoivat graafin rakennedatan perusteella muotoillun kuvan graafista. Muotoilualgoritmin perustana on joko solmujen hierarkkinen järjestäminen tai fysikaalisen jousimallin simulointi. Paketissa on myös yksinkertainen dotty-editori sekä muunnosohjelmat Graphvizin oman DOT-formaatin ja GXL:n välillä.
DOT-formaatti on minimalistinen XML-pohjaiseen GXL-kieleen verrattuna. Yksinkertaisia graafeja on helppo kirjoittaa vaikka käsin. Solmujen paikkoihin ei voi vaikuttaa, mutta muun tyyli- ja attribuuttitiedon (värit, fontit, solmujen muoto, solmujen ja kaarien tekstikuvaukset) kuvaukseen on monipuoliset mahdollisuudet. Myös DOT-muotoisten tiedostojen tuottaminen ohjelmallisesti on helppoa.
Graphviz-muotoilijat osaavat muotoilla tyylikkäästi jopa satoja solmuja sisältäviä graafeja, joskin syklejä sisältävillä graafeilla tuloksessa saattaa olla parantamisen varaa. Muotoilijoita voi konfiguroida monipuolisesti mm. kaarien keskimääräisen pituuden osalta, mikä saattaa parantaa lopputulosta. Monipuolisten ulostuloformaattien ansiosta graafien kuvat ovat julkaistavissa monissa eri ympäristöissä. Vaihtoehtoina ovat mm. tavanomaiset bittikarttaformaatit PNG, GIF ja JPG, vektoriformaatit EPS ja SVG ja jopa virtuaalimaailmojen kuvauskieli VRML. GXL-muunnosohjelman ja Xcm2kg-sovelluksen (katso luku 3.5.6) avulla graafeja voisi periaatteessa selata myös TouchGraphilla.
Tässä käsiteltyjä työryhmäohjelmistoja ei ole suunniteltu varsinaisiksi oppimisympäristöiksi, mutta niillä on laajat potentiaaliset käyttömahdollisuudet. Babylon chat ja Transdraw -ohjelmilla käyttäjäryhmällä on jaettu ''piirustuslauta'', joka avulla (erityisesti matemaattisten tai kuvallisten) ideoiden välitys onnistuu reaaliajassa. Projektin aikana ohjelmistoja ei tosin testattu käytännössä.
Wikit ovat WWW-sivustoja, joita niiden käyttäjät voivat editoida selaamisen yhteydessä. Wiki voidaan nähdä hypertekstitietokantana, koska kaikkiin siinä oleviin sivuihin voidaan viitata sivun nimellä ja wikiohjelmisto pitää kirjaa sivuista. Tämä mahdollistaa aidot kaksisuuntaiset linkit ja selkeän hakutoiminnon sivuston sisällä. Web-päiväkirjojen tapaan wikit ovat erittäin dynaamisia sivustoja verrattuna perinteisiin, tieteellisten artikkeleiden mallin mukaan rakennettuihin sivuihin. Wikien äärimmäisen hajautetun tuottamisen idea on osoittautunut toimivaksi, sillä wikiohjelmistojen ja eri erikoisalueille keskittyvien wikien määrä kasvaa jatkuvasti. Wikimuodossa on tuotettu henkilökohtaisia sivustoja, tietämyskantoja, oppikirjoja ja jopa virtuaalinen tietosanakirja Wikipedia32. [12]
Jotkut wikiohjelmistot sisältävät web-päiväkijaohjelmistojen piirteitä, jolloin wikistä tulee monen käyttäjän jaettu päiväkirja ja muistilista, jota ketkä tahansa käyttäjät voivat edelleen kommentoida ja laajentaa. Raportin kirjoittajan mielestä wikit voisivat toimia hyvin myös hajautettuna oppimisympäristöinä tai vaikkapa luentomateriaalien ja opiskelijoiden omien huomautusten ja kysymysten avoimena käyttötilana. Matematiikkaakin voidaan joissakin wikiymäristöissä esittää. Esimerkiksi Wikibooks-järjestelmään33 (katso luku 4.2) on mahdollista syöttää TEX-koodia, joka muunnetaan HTML:ksi tai kuviksi.
HMath34 on MathML-kieltä tukeva, avoimeen lähdekoodiin perustuva Java-pohjainen wiki- ja web-päiväkirjaohjelmisto. Se on laajennus SnipSnap-järjestelmälle35. Projekti on vasta noin kolmen kuukauden ikäinen eikä lähdekoodeja ole vielä julkistettu, mutta järjestelmällä on valtava potentiaali. Se on todennäköisesti ensimmäinen Wiki-tyylinen järjestelmä, joka tukee suoraan MathML:aa ja siten matematiikan julkaisua keskustelupalstan tyylisessä ympäristössä. MathML-kielen lisäksi järjestelmä tukee havainnollistusten luontia JavaView-sovelman (katso luku 3.1.3) avulla. Sivustolla olleet esimerkkikaavat näyttivät Mozillan MathML-latojalla katsottuna tyylikkäiltä (vaikka eivät aivan TEX-tasoa olleetkaan).
MathML-tuki on oleellista yhteistoiminnalle muiden sovellusten kanssa, mutta käsin kirjoitettuna MathML ei ole käytännöllistä. Suuremmat kaavat kannattanee luoda LATEXilla tai jollain kaavaeditorilla ja sitten kopioida wikiin. Toinen vaihtoehto olisi ehdottaa HMathin tekijöille jonkin TEX® MathML -muuntimen integrointia osaksi järjestelmää. Joka tapauksessa järjestelmä vaikuttaa lupaavalta ja sen kehitystä kannattanee seurata.
JSPWiki36 on toinen Java-pohjainen, avoimeen lähdekoodin perustuva wikiohjelmisto. Verkko-opetuksen kannalta kiinnostavinta on Danny Ayersin kehittämä Whiteboard-plug-in37, joka mahdollistaa SVG-grafiikan editoinnin suoraan sivulta. Tekstimateriaalin tapaan kaikki wikin käyttäjät voivat editoida SVG-kuvia, joskaan eivät samanaikaisesti. Tällä hetkellä SVG-editointitoteutus on varsin minimaalinen (ei erityisiä piirtotyökaluja, piirto tapahtuu vapaalla kädellä), mutta tekniikka kehittynee ja yleistynee idean keksimisen myötä. Jo nykyisellään SVG-piirroksiin voi lisätä tekstiä ja linkkejä.
Babylon Chat38 on Andy McLaughlinin kehittämä Java-pohjainen, avoimen lähdekoodin piirustuslauta- ja chat-ohjelma. Ohjelmassa on tarjolla peruspiirtotyökalut (vapaan käden piirto, suorakulmiot, ympyrät, teksti, leikepöytäkuvat), Chat-toiminto tukee yleistä tai kahdenkeskistä keskustelua. Babylon chatia voi käyttää Java 1.3 -sovelmana, joka on yhteydessä erilliseen palvelimeen. Kotisivuilla luvataan ohjelman toimivan periaatteessa mielivaltaisen suurilla käyttäjämäärillä, mutta ennen laajamittaista käyttöä ohjelma pitäisi kuormitustestata [20].
TransDraw39 on Université catholique de Louvainissa kehitetty, verkkoympäristössä toimiva vektoripohjainen piirto-ohjelma. Ohjelma on saatavilla lähdekoodeineen Windows- ja Unix-käyttöjärjestelmille. Piirto on synkronoitu siten, että kaikki verkossa olevat näkevät saman kuvan ja editoinnit päivittyvät välittömästi. Babylon Chatista poiketen järjestelmässä on hajautettu arkkitehtuuri, eli erillistä palvelinta ei ole.
Projektin aikana suunnittelijat laajensivat olemassa olevia ohjelmistoja ja kehittivät muutamia uusia sovelluksia, merkittävimpänä Tero Tiluksen Henkari-järjestelmä. Raportin kirjoittajan työajasta merkittävä osa meni Xcm2kg-muunnosohjelmaan.
Henkari on Tero Tiluksen kesällä 2002 [20] kehittämä PHP-pohjainen järjestelmä web-sivuston navigointiin ja ylläpitoon. Järjestelmä on julkaistu vapaaohjelmana (GPL). Se on käytössä mm. matematiikan approbaturin sivuilla40 ja matematiikan yleisopintojen sivuilla41. Sivuston ulkoasu määritetään sivupohjilla, joihin järjestelmä lisää tarvittaessa automaattisesti navigointipuun ja näyttää hakemistopolun. Sivujen sisältö on erillisissä työtiedostoissa. Henkari hoitaa automaattisesti niiden asettelun sivustopohjaan ja lisäämisen navigointipuuhun. Eri tiedostotyypeille voidaan määritellä erityisiä käsittelijöitä, jotka ajetaan ennen sivun näyttämistä. Henkari sisältää myös välimuistin, eli sivuja ei generoida jokaisella kyselyllä uudestaan.
Käsittelijät (tällä hetkellä mm. html-tiedostoille, php-tiedostoille, ejsc-havainnollistuksille ja pakatuille tar.gz-tiedostoille) mahdollistavat mm. opetusmateriaalin helpon tuottamisen. Esimerkiksi ejsc-käsittelijä hoitaa koodin kääntämisen ejscc-kääntäjällä (katso luku 3.5.2) ja sen muotoilemisen sovelmasivuksi. Periaatteessa olisi mahdollista tehdä myös TouchGraph-käsittelijä, joka joka lukee TouchGraphin XML-tiedostoja ja muodostaa linkkiselaimen sisältävän sivuston sen pohjalta.
Ejsc (Extended Java Sketchpad Construction) on Tero Tiluksen kesällä 2002 [20] Java Sketchpadin (katso luku 3.1.2) jsc-kielen pohjalta kehittämä laajennus Java Sketchpad -havainnollistusten kirjoittamiseen. Ejscc on C-kielellä kirjoitettu kääntäjä, joka kääntää ejsc-tiedostoja jsc-muotoon. Kääntäjä on julkaistu vapaaohjelmana (GPL). Laajennuskieli on yhteensopiva jsc-tiedostojen kanssa ja tukee lisäksi muuttujia, funktioita ja ohjausrakenteita. Lisäksi ejsc-tiedostojen esikäsittelyssä voi käyttää valinnaisesti C-kielen esikääntäjää.
Splitter on Tero Tiluksen keväällä 2002 [20] kehittämä, vapaaohjelmana (GPL) julkaistu Python-skripti FrameMaker-ohjelmistolla tehtyjen HTML-dokumenttien pilkkomiseen. Ohjelmaa on käytetty mm. talousmatematiikan kurssin opetusmateriaaleihin. FrameMakerilla laadittu materiaali on alunperin yhdessä tiedostossa, jonka Splitter jakaa otsikoiden mukaan moneen tiedostoon ja lisää navigoinnin.
LATEXEq on Tero Tiluksen syksyllä 2002 [20] kehittämä, PHP- ja Bash-skripteistä koostuva kokeellinen sovellus kuvien generointiin LATEX-kaavoista WWW:ssä. Kuva generoidaan muuntalla LATEX-ajosta saatava DVI-tiedosto ensin PS-muotoon, jonka jälkeen leikataan siitä reunat pois ja muutetaan rasterimuotoon Convert-ohjelmalla.
LATEX-kaavakieltä tunteville sovellus on helppo ja nopea käyttää, mutta LATEXin kielen ilmaisuvoimasta johtuen (esim. makrot, ulkoisten tiedostojen koostaminen koodiin) muunnoksessa on potentiaalinen tietoturvaongelma. Ratkaisu tietoturvaongelmaan voisi olla hyväksytyn komentojoukon rajoittaminen vain matemaattisiin komentoihin (esim. DesignSciencen tuotteissa käytetään LATEX-kielen osajoukkoa WebTeX, joka saattaisi olla tutkimisen arvoinen). Toinen mahdollinen ratkaisu on LATEX-koodin muuntaminen MathML-muotoon (esim. TeX4ht:lla, katso luku 3.2.3) ja generoida kuva MathML:stä.
S8board42 on Kelli Shaverin kehittämä, PHP-pohjainen vapaaohjelmana (GPL) julkaistu viestipalsta. TeXOnline (työtiedostoissa nimellä mbwo, messageBoard With Objects) on Tero Tiluksen keväällä 2002 kehittämä kokeellinen oliotietokanta, jossa säilytetään LATEXilla luotujen kaavojen kuvia (ja tarvittaessa luodaan uusia). Tekemällä S8boardiin pieniä muutoksia ja yhdistämällä sen TEXOnlinen oliotietokantaan tuloksena saatiin TEX-kaavakieltä ymmärtävä viestipalstaprototyyppi. Todellisesta käyttöä rajoittaa se, että jokainen kaava käytyy käydä luomassa manuaalisesti oliotietokantaan. [20]
Xcm2kg on kesällä 2003 kehitetty, vapaaohjelmana (LGPL) julkaistu Javalla toteutettu muunnosohjelma, joka muuntaa IHMC Concept Map Tool -käsitekarttaohjelman (katso luku 3.3.1) XML-ulostuloformaatin mukaiset käsitekartat KeyGraph-graafikäyttöliittymän formaattiin (katso luku 3.5.7). KeyGraph on TouchGraph-käyttöliittymän laajennus, jonka formaattia on hieman laajennettu alkuperäiseen verrattuna. Xcm2kg:n tuottamia tiedostoja voi tarkastella myös alkuperäisessä TouchGraph-sovelluksessa, tosin kaarien selitetekstit eivät näy.
Käsitekarttaan liittyvät resurssit käännetään KeyGraph-graafissa vinkki-ikkunassa näkyviksi URL-linkeiksi. Matematiikan esittämisen kannalta oleelliset kaavakuvat voidaan määritellä näkymään suoraan vinkki-ikkunassa merkitsemällä niiden kuvaustekstin alkuun in_-etuliite. Myös URL-linkeistä voidaan määrittää, ovatko ne sisäisiä (aukeavat samaan selaimeen) vai ulkoisia (avaavat uuden selainikkunan) merkitsemällä kuvaustekstin alkuun ext_. Käsitekarttoihin menevät linkit siirretään muunnosohjelmassa map.php-tiedoston alle, jonka avulla käyttäjät pääsevät tutkimaan paikallisia käsitekarttoja WWW:ssä.
Xmc2kg:n muunnos suoritetaan kahdessa vaiheessa siten, että ensin IHMC:n XCM-formaatti muunnetaan GXL-väliformaattiin, jonka jälkeen GXL-muoto muunnetaan KeyGraphin XML-tiedostoksi. Ensimmäisesssä muunnoksessa käytetään JGraph-projektin kehittämää JGraphPad43-komponenttia. GXL-formaatin käyttö muunnosprosessissa mahdollistaa periaatteessa minkä tahansa GXL-tiedoston muuntamisen TouchGraphin ymmärtämään formaattiin. Attribuuttitietojen, kuten selitetekstien esittämisessä voi olla eroja eri lähteistä saaduissa GXL-tiedostoissa, mutta ainakin graafin rakenne on kuvattavissa. Muunnosprosessi on esitetty kuvassa 3.1.

KeyGraph on syksyllä 2003 kehitetty laajennus Alex Shapiron kehittämään TouchGraph LinkBrowser -sovellukseen (katso luku 3.3.3) ja sen formaattiin. Käyttöliittymään lisättiin tuki näppäimistöohjaukselle nuolinäppäimillä. Kaariin lisättiin mahdollisuus selitetekstille. Lisäksi URL-linkkien avaukseen ja graafien konfigurointiin tehtiin pieniä korjauksia.
TopicTree on vuoden 2003 aikana viimeistelty PHP/JavaScript-pohjainen, avoimen lähdekoodin (GPL/LGPL/MPL1.1) sovellus puurakenteiden hallintaan. Sovellus toimi alunperin raportin kirjoittajan linkkilistana, mutta sitä voi käyttää myös yksinkertaisena hahmotelmatyökaluna. Käyttöliittymä perustuu hierarkkiseen listaan, jonka solmuja voi selata nuolinäppäimillä tai hiirellä. Listassa näytettävät tiedot muuttuvat aktivoitujen solmujen mukaan työpöytäsovellusten puukomponenttien tapaan.
TopicTree-sovellusta on mahdollista käyttää hajautettuna suunnitteluympäristönä: puussa olevat tiedot ovat kenen tahansa muutettavissa ja myös toisella WWW-palvelimella olevan TopicTree-puun voi linkittää omaan puuhun. Jokainen solmu kuuluu johonkin aiheeseen ja voi sisältää tekstiä, linkkejä selitteineen tai lisää aiheita. Jokainen aihe tallennetaan omaan tiedostoonsa yksinkertaisella tekstiformaatilla (itse asiassa käyttäjät pääsevät editoimaan suoraan datatiedoston sisältöä tietoja päivitettäessä).
Sovelluksen puukäyttöliittymä ei ole sidottu linkkilistoihin, vaan sitä voi käyttää periaatteessa mihin tahansa hierarkkiseen tietoon. Puun loogiset solmut määritetään parin CSS-tyyliluokan avulla, eli niiden ei tarvitse olla edes listoja. Esimerkiksi FreeMind-ohjelmaan (katso luku 3.3.2) tehty paranneltu HTML-ulostulo käyttää TopicTreen käyttöliittymää.
TopicTree-sovelluksen tietomalli on tulkittavissa myös aihekartaksi (mutta ei päinvastoin): aihe vastaa aihekartan aiheen tyyppiä, aiheen sisällä olevat selitteet vastaavat aihekartan aiheita ja selitteiden linkit esiintymiä. Aiheiden sisällä olevat aiheet vastaavat yli- ja alityypitystä. TopicTree-paketissa onkin mukana yksinkertainen PHP-skripti, joka muuntaa datatiedostot yhdeksi XML-muotoiseksi aihekartaksi. Muunnettua aihekarttaa voi selata esim. Omnigator-selaimessa (katso luku 2.5.3. Näin TopicTreeta voi käyttää myös yksinkertaisten aihekarttojen tuottamiseen.
Mozillan MathML-tuen parantuessa matematiikan esittäminen MathML-kielellä HTML:n lomassa on pian realistinen vaihtoehto. HMath-wiki (katso luku 3.4.1) on hyvä esimerkki toimivasta matemaattisen tekstin luonnollisesta esittämisestä WWW:ssä. Sen pohjalle voisi rakentaa esimerkiksi viestipalstan tai vaikka oppimisympäristön. Selainten MathML-tuen parantumisesta huolimatta ongelmaksi jää edelleen kaavojen syöttö. MathML ei ole käytännöllistä käsin kirjoitettavaksi, joten jonkin kaavaeditorin (Design Science?) tai TEX® MathML -muunnosohjelman integrointi viestipalstalle olisi toivottavaa. Myös SVG-grafiikan piirto olisi hyödyllinen ominaisuus hieman Whiteboardin (katso luku 3.4.2) tapaan, mutta useammilla piirtotyökaluilla varustettuna.
Xcm2kg-muunnosohjelman valmistumisen myötä käsitekarttojen tuottaminen ja käyttö WWW-sivuilla on suhteellisen yksinkertaista. Niiden käyttö suoraan esim. kurssimateriaalin osana helpottuisi entisestään integroimalla TouchGraph Henkarin osaksi uuden käsittelijän muodossa. Käsittelijä voisi ottaa vastaan suoraan IHMC-käsitekarttaohjelman (katso luku 3.3.1) XCM-tiedoston, ajaa Xcm2kg:n ja tuottaa sovelmasivun, joka näyttää graafin.
Touch/KeyGraph-graafikäyttöliittymää voisi kehittää edelleen lisäämällä linkkiselaimeen hakutoiminnon ja selaushistorian. Tällöin laajojen graafien selaus onnistuisi helpommin. Käyttöliittymää voisi kokeilla myös osana WWW-oppikirjan navigointia (Xcm2kg-paketissa on tästä pienimuotoinen esimerkki). Tällöin graafi pitäisi pyrkiä tuottamaan automaattisesti oppikirjan luvuista, määritelmistä, todistuksista ja mielellään myös määritelmien ja todistusten välisistä riippuvuussuhteista.
OPML ja GXL ovat yksinkertaisia, toimivia formaatteja tekstipuiden ja graafimuotoisen tiedon käsittelyyn. Niille on jo nyt saatavia useita sovelluksia, joita kannattaa tutkia edelleen. GXL-kieltä tukevien sovellusten graafit ovat muunnettavissa Xcm2kg-ohjelman avulla (tai hyvin pienellä lisätyöllä) TouchGraphin formaattiin. TopicTree-sovellukseen voisi lisätä OPML-tuen, mikä laajentaisi sen käyttömahdollisuuksia.
Matemaattista opetusmateriaalia, oppikirjoja, oppimisympäristöjä ja interaktiivia tehtäviä on saatavilla verkosta niin runsaasti, ettei niiden kattava käsittely ole tässä mahdollista. Sen sijaan keskitytään käsittelemään yleisesti suurimpia opetusmateriaalikokoelmia ja yleiskäyttöisiä matemaattisia kirjastoja.
MathWorld44 on Eric Weissteinin kokoama ja Wolfram-yhtiön sponsoroima laaja matematiikan WWW-hakuteos, johon on kategorisoitu kattavasti matematiikan eri alat ja niiden käsitteet. Käsitteet on linkitetty toisiinsa, havainnollistuksina käytetään kuvia ja LiveGraphics3D-havainnollistuksia (katso luku 3.1.3). Sivut ovat kuviksi konvertoiduista kaavoista huolimatta selkeitä ja sivusto soveltuu hyvin hakuteokseksi. Oppikirjoja se ei kuitenkaan korvaa.
Math Forum45 on Drexelin yliopiston ylläpitämä sivusto, joka keskittyy matematiikkaan ja erityisesti sen opetukseen liittyviin resursseihin. Sivusto sisältää erittäin laajan WWW:ssä olevan matemaattisen materiaalin linkkikokoelman. Materiaali on kategorisoitu matematiikan alojen, resurssityyppien, matematiikan opetukseen liittyvien aiheiden ja koulutustason mukaan.
AMS Math on the web46 on AMS-organisaation ylläpitämä linkkikokoelma WWW:n matematiikkaresursseista. Näkökulma on hieman edellisiä kirjastoja laajempi käsittäen artikkelien ja opetusmateriaalien lisäksi matemaatikkojen yhteystietoja, matematiikan laitoksia, bibliografioita, (WWW:ssä julkaistua ja painettua) kirjallisuutta sekä kausijulkaisuja. Luonnollisesti mukana on myös TEX-linkkejä.
HELM47 (Hypertextual Electronic Library of Mathematics) on Bolognan yliopiston tietojenkäsittelytieteen laitoksen projekti, jonka tarkoituksena on luoda matemaattisen tietämyksen kattava digitaalinen kirjasto. Muista tällä hetkellä olemassa olevista digitaalisista kirjastoista poiketen matemaattinen tieto syötetään järjestelmään formaalissa muodossa, jolloin tietokone pystyy laskemaan annetuilla kaavoilla ja käsittelemään todistuksia. HELM-projektin sivuilla oleva prototyyppi oli vielä melko hankala käyttää eikä sellaisenaan sovellu opiskeluun, mutta projektin tavoitteet ovat kiinnostavia.
Suurin osa WWW:ssä olevista metematiikan oppikirjoista on PDF- tai PS-muotoisia, todennäköisesti LATEX-koodista generoituja. Ne soveltuvat hyvin paperikäyttöön mutta huonommin tietokoneen ruudulle. Verkko-opetuksen kannalta kiinnostavampia ovat hypertekstikirjat, joiden sisältö on jaettu moneen tiedostoon ja teksti on linkittynyttä (mieluiten käsitteiden välillä, ei pelkästään sisällysluettelosta koostettu navigointi).
Kotimaisista matematiikan hypertekstikirjoista tunnetuin lienee MatTa-projektin kehittämä \mathfrakM niinkuin matematiikka (tai lyhyesti Iso-M) [10] - lukiotasoisen matematiikan digitaalinen kertauspaketti. Iso-M sisältää n. 100 matematiikan tehtävän vihjeistetyn kokoelman (muotona HTML+kaavakuvat) sekä n. 400 sivua käsittävän lukiotason matematiikan tietosanakirjan (toisiinsa linkitettyjä PDF-tiedostoja). Tehtävät on suunniteltu ratkaistavaksi jollakin laskentaohjelmalla. Paketti on suunniteltu itseopiskeluun, mutta sopivasti organisoimalla se soveltuu myös kurssimateriaaliksi. [8]
Hypertekstikirjoja löytyi WWW:stä huomattavan vähän. Edellä mainitun Iso-M:n lisäksi MathWorldia (katso luku 4.1) voidaan pitää sellaisena, joskaan se ei ole varsinaisesti oppikirja. Eräs kohtuullinen esimerkki on J. Beachyn and W. Blairin oppikirjoihin perustuva Abstract Algebra On-Line48, yliopistotason algegran oppikirja. Sivusto sisältää tavanomaisen sisällysluettelon lisäksi linkit kirjan määritelmiin ja todistuksiin. Sivustoa voi selata kehyksillä, jolloin sisällysluettelo on jatkuvasti näkyvissä ja esim. määritelmien kertaaminen on helppoa.
WWW:n hypertekstitystä vielä paremmin hyödyntävä järjestelmä hyödyntäisi käsitteiden välisiä suhteita linkityksissä ja ennen kaikkea listaisi todistuksissa hyödynnettävät aiemmat lauseet ja lemmat kootusti. Tällaisia oppikirjoja ei WWW:stä löytynyt, joskin ActiveMath-oppimisympäristö (katso luku 4.3.1) pyrkii toteuttamaan ideaa. Toinen todistusketuja havainnollistava sivusto on MetaMath49, joka on samalla kieli teoreemojen ja todistusten kuvaamiseen. Sen avulla on generoitu tuhansia täysin formaaleja todistuksia käsittävä sivusto, jonka jokaisen todistuksen askeleet voidaan jäljittää hyperlinkkien avulla aksioomiin asti. Sivusto ei sovellu opetusmateriaaliksi (mahdollisesti matemaattisen logiikan kursseja lukuunottamatta) mutta toteuttaa erinomaisesti idean linkitetyistä todistuksista.
Ulkoasultaan perinteisten oppikirjojen kaltainen, mutta toteutustavaltaan täysin uudenlainen tapa ovat Wiki-kirjat50 (Wikeistä enemmän katso luku 3.4). Ne ovat ilmaisia, vapaaehtoisten kollektiivisesti kirjoittamia oppikirjoja, joita kuka tahansa voi editoida ja kehittää edelleen. Wikibooks-järjestelmä tukee myös matematiikan kirjoitusta TEX-koodilla. Kaavat esitetään sivuilla HTML-koodina tai kuvina.
Erilaisia virtuaalisia oppimisjärjestelmiä on runsaasti saatavilla, useimmat niistä ovat kaupallisia. Niiden yleisenä ongelmana on, etteivät ne tue matemaattista tekstiä. Tässä luetellut oppimisympäristöt keskittyvät valtavirrasta poiketen matematiikan opiskeluun. Yleiskäyttöisistä oppimisympäristöistä mainittakoon Taideteollisen korkeakoulun medialaboratoriossa kehitetty FLE51. Oppimisympäristö on toteutettu ZOPE-sovelluskehittimellä ja Python-kielellä ja se on julkaistu vapaaohjelmana (GPL). Laajasti käytössä ovat myös Jyväskylän yliopiston Koulutuksen tutkimuslaitoksen koordinoiman peda.net-projektin52 verkkotyövälineet.
Activemath53 on adaptiivinen ja interaktiivinen matematiikan ympäristö. ActiveMathia kehitetään Deutsche Forschungszentrum für Künstliche Intelligenz -tutkimuskeskuksessa ja Saarlandin yliopistossa. Järjestelmän kehitys on vielä melko varhaisessa vaiheessa, osittain toimiva (lupaavan näköinen) demoversio on selattavissa verkossa, mutta ympäristöä voi voi ladata eikä lähdekoodeja ole saatavilla (myöskään palvelimen lisensoinnista ei ole tietoa). Todennäköisesti ympäristö kaupallistetaan sen kehittyessä.
Järjestelmän perustana on MBase-tietämyskanta, joka sisältää OmDoc-muodossa järjestelmän tuntemat matemaattiset oliot. Muissa opetusmateriaaleissa tyypillisesti käytetyn LATEX- tai HTML-koodin sijaan materiaalin sisältö on erotettu sen esitystavasta, mikä mahdollistaa adaptiivisen opetusmateriaalien luonnin: opiskelija voi itse asettaa oppimistavoitteensa (mahdollisesti opettajan antamien reunaehtojen mukaan) ja valita, millä tarkkuustasolla eri asiakokonaisuuksia käsitellään. valintojen perusteella opiskelijalle luodaan dynaamisesti oma oppikirja tietämyskannasta. Järjestelmän oppikirjat ovat HTML-muotoisia.
Järjestelmän tehtäviä voidaan laskea ulkoisilla matematiikkaohjelmilla järjestelmästä käsin. Tuettuja ohjelmia ovat mm. MuPad ja Maple. Ohjelmia käytetään Java-sovelmassa olevan komentorivin välityksellä. Opettaja voi seurata opiskelijan antamia komentoja ja tarvittaessa neuvoa häntä verkon yli. Käyttäjillä on oppimisprofiilit, joilla opettaja voi mm. seurata tehtävien suoritusta ja oppimistavoitteiden toteutumista. [13]
MathWeb-organisaation kehittämä OmDoc-kieli54 on laajennus MathML- ja OpenMath-kielille (katso luku 2.3). Se on suunniteltu matemaattisten dokumenttien kokonaisvaltaiseen esittämiseen sisältäen tekstin, kaavojen ulkoasun, kaavojen semantiikan ja dokumentin metatiedot (kieli, tekijä, käyttöoikeus ym). Kielessä on tuki yleisille matemaattisessa tekstissä esiintyville kokonaisuuksille, kuten määritelmä, lause, todistus, esimerkki jne. Määritys on ymmärrettävästi varsin laaja, OmDocin mukaisen matemaattisen tekstin kirjoittaminen käsin on jopa hankalampaa kuin MathML:n kirjoittaminen. Tietämyskannan formaattina ja ohjelmallisesti tuotettuna sen käyttö on kuitenkin perusteltua, koska se mahdollistaa monipuolisten hypertekstikirjojen luonnin ja niissä olevien kaavojen suoran käytön matematiikkaohjelmissa. [11]
WWW Interctive Mathematics Server55 (WIMS) on Xiao Gangin kehittämä, vapaaohjelmistona (GPL) julkaistu matematiikkapalvelin WWW-ympäristöön. Järjestelmää käytetään C-kielisen CGI-skriptin avulla, joka prosessoi käyttäjien pyynnöt ja välittää ne eteenpäin WIMS-moduuleille. Moduulit ovat itsenäisiä sovelluksia, jotka on kirjoitettu WIMSin omalla skriptikielellä. Varsinainen laskenta suoritetaan erillisillä laskentaohjelmilla, joita käytetään standardeilla rajapinnoilla. Modulaarinen rakenne takaa järjestelmän laajennettavuuden. Palvelinta käytetään tavallisten HTML-lomakkeiden avulla.
Palvelin tukee verkko-opetusta ns. virtuaalisten luokkien avulla. Virtuaaliset luokat ovat tehtäväkokoelmia, jotka vaativat kirjautumisen käyttäjiltä. Luokalla on vastuullinen opettaja, joka voi seurata tehtävien suoritusta. Myös suoritustilastojen ja pisteiden laskeminen on mahdollista. Keskustelua tai ohjausta verkon välityksellä järjestelmä ei tue. Palvelin sisältää laajahkon kokoelman valmiita tehtäviä ja sovelluksia. Modulaarisen arkkitehtuurin ja avoimen lähdekoodin ansiosta myös uusien sovellusten tekeminen ja integrointi laskentasovelluksiin onnistuu. [7]
Maths online56 on F. Embacher ja P. Oberhuemer kehittämä, kaikille koulutustasoille suunnattu laajahko interaktiivinen matematiikan tehtäväkokoelma. Tehtävät on toteutettu Java-sovelmina. Sivustolla on myös työkaluja omien tehtävien toteuttamiseen ja runsaasti linkkejä WWW:ssä oleviin muihin opetusmateriaaleihin. Tehtäväkokoelma on vapaasti levitettävissä ja se onkin käytössä varsin monessa oppilaitoksessa ympäri maailmaa, Suomessa ainakin Lappeenrannan teknillisessä yliopistossa57.
Raportissa kuvattiin matematiikan verkko-opetusprojektin toimintaa ja tuotoksia keskittyen ajalle 1.4.-31.12.2003. Projektin tutkimuskohteina olivat erityisesti matemaattisen tekstin julkaisuprosessit WWW:ssä ja matemaattisen tiedon esitys käsitteellisellä mallintamisella. Lisäksi tutkittiin olemassaolevia aiheeseen liittyviä ohjelmistoja ja tarvittaessa kehitettiin uusia.
Tuleva standardi matemaattisen materiaalin esittämiseen WWW:ssä lienee XHTML:n, MathML-kaavojen ja SVG-vektorigrafiikan yhdistelmä (katso luku 2.3). Näistä kahta jälkimmäistä selaimet tukevat vielä melko huonosti, mutta Mozillaan ollaan toteuttamassa natiivia tukea kummallekin määritykselle. Näistä MathML-tuki toimii jo suhteellisen hyvin edellyttäen, että tietokoneelle on asennettu matematiikkafontit. Kaikille selaimille on saatavilla myös ilmaisia plug-ineja MathML:n ja SVG:n esittämiseen.
Kesällä 2003 projektissa testattiin interaktiivista matematiikkaohjelmaa LiveMathia (katso luku 3.1.1. WWW:ssä olevista käsitekarttaohjelmista IHMC Concept Map tool (katso luku 3.3.1) osoittautui sopivaksi ohjelmaksi käsitekarttojen tuottamiseen ja TouchGraph (katso luku 3.3.3) niiden esittämiseen. Kesällä ja syksyllä 2003 kehitettiin muunnosohjelma näiden välille. Lisäksi TouchGraph-graafikäyttöliittymää paranneltiin. Työkalut helpottavat käsitekarttojen käyttöä verkko-opetuksessa.
Wikit (katso luku 3.4) ovat WWW-sivustoja, joita niiden käyttäjät voivat editoida selaamisen yhteydessä. Wikit mahdollistavat erittäin tehokkaan sisällön tuottamisen ja kollektiivisen tiedon jakamisen verkossa. HMath (katso luku 3.4.1) on wiki/web-päiväkirjajärjestelmä, joka mahdollistaa MathML-kaavojen kirjoituksen teksteihin. Järjestelmää voisi kokeilla jollakin kurssilla - voisiko wiki toimia koulutuksessa epämuodollisena viestintä- tai opetusvälineenä?
Verkossa julkaistavat matematiikan materiaalit tulisi tuottaa WWW:n hypertekstimäisyyttä ja käsitteellistä mallinnusta hyödyntäen. Materiaalissa esiintyvät määritelmät ja todistukset tulisi voida listata erillisinä ja käsitteiden väliset suhteet tulee ilmaista tietokoneen ymmärtämässä muodossa. Erityisesti todistusten välisten riippuvuussuhteiden merkintä on tärkeää, koska silloin todistusketjua voidaan havainnollistaa automaaattisesti. Esimerkkejä toteutetuista hypertekstikirjoista on luvussa 4.2. Mahdollinen toteutuskieli materiaaleille voisi olla OmDoc (katso luku 4.3.1).
WWW-linkit viitattu 15.1.2004.
1 "http://www.integretechpub.com/"
2 "http://www.dessci.com/en/products/mathtype/"
3Ks. "http://www.w3.org/Graphics/SVG/" ja "http://www.w3.org/Math/"
4Ks. "http://www.mozilla.org/projects/svg/" ja "http://www.mozilla.org/projects/mathml/"
6Ks. "http://john.redmood.com/organizers.html" ja "http://john.redmood.com/brainstorming.html"
8ISO/IEC 13250
10 "http://www.ontopia.net/download/index.html"
12 "http://matta.hut.fi/matta/viitteet.shtml"
14 "http://www.maths.jyu.fi/matappro/LiveMath/"
15 "http://www.keypress.com/sketchpad/java_gsp/"
16 "http://www.maths.jyu.fi/ylemat/opetusmateriaali/havainnollistuksia/"
17 "http://www.vis.uni-stuttgart.de/ kraus/LiveGraphics3D/"
18 "http://www-sfb288.math.tu-berlin.de/vgp/javaview/"
19 "http://www.dessci.com/en/products/webeq/"
20 "http://www.wolfram.com/products/webmathematica/"
21 "http://integrals.wolfram.com/"
22 "http://www.imagemagick.org/"
23 "http://www.hj-gym.dk/ hj/writer2latex/"
24 "http://www.cis.ohio-state.edu/ gurari/systems.html"
25 "http://hutchinson.belmont.ma.us/tth/"
26 "http://www.schemasoft.com/mathml/"
27 "http://xml.apache.org/batik/"
29 "http://freemind.sourceforge.net"
30 "http://touchgraph.sourceforge.net"
31 "http://www.research.att.com/sw/tools/graphviz"
32 "http://en.wikipedia.org/wiki/Wiki"
33 "http://wikibooks.org/wiki/Wikibooks:TeX_markup"
35 "http://snipsnap.org/space/start"
36 "http://www.jspwiki.org/Wiki.jsp"
37 "http://dannyayers.com/2003/08/jspwiki/whiteboard.htm"
38 "http://visopsys.org/andy/babylon/"
39 "http://www.info.ucl.ac.be/people/ned/transdraw/transdraw.html"
40 "http://www.maths.jyu.fi/matappro"
41 "http://www.math.jyu.fi/ylemat/"
42 "http://www.hotscripts.com/Detailed/9204.html"
43 "http://www.jgraph.com/resources.html"
44 "http://mathworld.wolfram.com/"
46 "http://www.ams.org/mathweb"
48 "http://www.math.niu.edu/ beachy/aaol/"
50 "http://wikibooks.org/wiki/Mathematics_bookshelf"
53 "http://www.activemath.org/"
54 "http://www.mathweb.org/omdoc/"
55 "http://math.cochise.edu/ wims/wims.cgi/ wims.cgi"
56 "http://www.univie.ac.at/future.media/moe/"
57 "http://www.it.lut.fi/mat/virtuaali/"