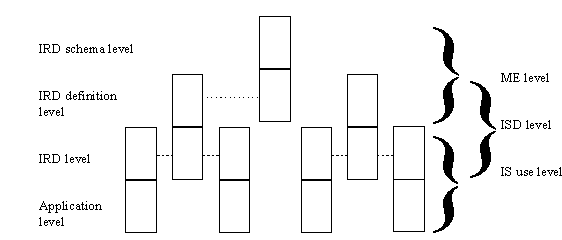This section discusses metamodels and metamodeling languages as used in this thesis to describe tool-supported modeling techniques. This discussion is important because all ME is based on some formalism and because it deals with our research question on modeling method knowledge. Accordingly, in the next subsections we shall define metamodels and metamodeling. This is followed by a representation of different types of metamodels, and especially metamodels which are based on semantic data models.

Models play a crucial role in ME, as in all engineering. Only those aspects of a method can be engineered which can be made explicit through a representation. Modeling of methods is not important only in constructing methods, but has also proven to have advantages in systematizing and formalizing weakly defined methods (Tolvanen and Lyytinen 1993), providing a more “objective” approach to comparing methods (Hong et al. 1993, Rossi and Brinkkemper 1996), supporting standardization efforts (e.g. Booch et al. 1997, OMG 1997), and examining linkages between ISD methods and programming languages (Hillegersberg 1997). Metamodeling is also successfully used in building flexible modeling tools (Kelly 1997, Kelly and Smolander 1996), interfaces between tools (CDIF 1997), and repository definitions (CASE Outlook 1989). Metamodels can differ greatly based on their purpose and the type of method knowledge considered. For example, Brodie (1984) analyzed various semantic data models and showed that there is a need for application-specific data models. Similarly, the ME frameworks and underlying metamodels focus on different types of method knowledge (cf. Section 3.2.2).

In its simplest form we can say that a metamodel is a conceptual model of an ISD method (Brinkkemper 1990). Metamodels can be further divided into different types depending on what type of method knowledge is modeled. Hereafter, we use the term metamodel to refer to a meta-data model which describes the static aspects of a method. 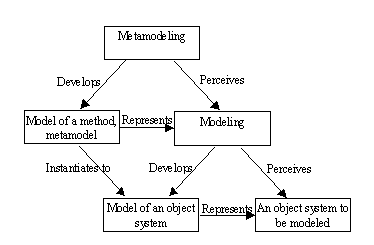Consequently, metamodeling can be defined as a modeling process which takes place one level of abstraction and logic higher than the standard modeling process (van Gigch 1991). The relationships between modeling and metamodeling are illustrated in Figure 3-3.

FIGURE 3-3 Metamodeling and modeling (after Brinkkemper 1990).

In metamodeling, the focus is on method knowledge applied in modeling. In the case of meta-data modeling this means the conceptual structure and notation of the method. Accordingly, the resulting metamodel captures information about the concepts, constraints, rules and representation forms used in modeling techniques. IS developers use this knowledge — although often unconsciously — in IS modeling tasks (see Smolander et al. 1990). Clearly, no modeling is possible without some sort of (explicit or implicit) metamodel. The same is also true for metamodeling as it also uses its own methods and tools which, in turn, can be described one level higher in metametamodels (and so ad infinitum).

Kotteman and Konsynski (1984) show that at least four levels of instantiation are necessary to integrate the modeling of the usage and evolution of ISs. A similar observation underlies the architecture of the ISO IRDS (Information Resources Dictionary Standard, (ISO 1990)), and in the universal framework for information activities by Auramäki et al. (1987). The levels and their hierarchy are illustrated in Figure 3-4.

FIGURE 3-4 ISO IRDS repository framework.

The application level includes application data and program execution. An example of the former could be “Juha-Pekka Tolvanen” and an example of the latter the procedure by which this data has been added or removed in the application. This level corresponds to the instances of class-based languages and to instantiations of an IS model.

The IRD level includes database schemata and application programs, plus any intermediate specifications, and also specifications of non-computerized activities (e.g. business processes and work flows). This corresponds to the class level of class-based languages and instantiations of a metamodel (i.e. IS models). An example of the information at this level would be a definition of “customer” information as part of the database schema.

The IRD definition level specifies the languages in which schemata, application programs, and specifications are expressed. It may also contain the specification of possible static and dynamic inter-relationships between these languages, for instance how various design models are linked. This corresponds to the metaclass level of languages such as Smalltalk, and instantiations of a metametamodel (i.e. metamodels). An example of the information at this level would be the specifications of the ER diagram technique and its component types, such as “entity” or “cardinality”.

Finally, the IRD Definition Schema Level specifies a metametamodel according to which the IRD Definition level objects can be described and interlinked. An example would be ‘concept’ (Wijers 1991) or OPRR’s ‘Object’ metatype (Smolander 1992).

As the right side of the figure illustrates, these four levels can be grouped into interlocking level pairs. The interlocking is necessary since making sense of instances is not possible without type level information. To illustrate the interlocking pairs in Figure 3-4 the boxes are joined, and to represent that the number of instances is normally greater than the number of types the figure is in the shape of a pyramid. Thus, the hierarchy can be understood as being instantiations in which the higher level forms the type definitions for the lower level instances, in the same way as classes define objects, and metaclasses define classes. A level pair can also be intuitively understood as a database where the upper level is the schema and the lower level the database state.

The lowest pair, IS use, corresponds to application databases, consisting of a schema and of a database state used in daily business. At the database state level the data element “Juha-Pekka Tolvanen” is useless if its type information is not known (e.g. row in a customer table of a database). The middle pair, ISD, corresponds to data dictionaries or CASE tool repositories used to store models of IS. IS modeling tools also operate at this level. For example, an ER diagram describes a “customer” as an entity. The topmost pair, ME, corresponds to meta databases, such as metaCASE tools or CAME tools which store models of methods, i.e. metamodels. Here the metamodeling language plays the role of type information and modeling technique metamodels are viewed as instances. For example, an “entity” is described as an object type, an instance of the metatype ‘Object’, in an ER diagram metamodel. On the ISD level, types included in a metamodel determine what one can observe or describe about the application level while using the method.

Our research questions focus on the topmost pair of the IRDS framework. The first question on metamodeling constructs seeks to find applicable concepts and constraints for metamodeling languages, i.e. to define metametamodels. In other words, metametamodels provide constructs for metamodeling languages. The second research question on incremental ME deals with how the applicable instances of the ME level, i.e. metamodels can be recognized and constructed for ISD. Hence, the research itself can be placed above the IRD schema level, i.e. on a fifth level.

Although we mostly operate with concepts of the ME level we sometimes need to refer also to instances on the ISD level. To distinguish the concepts and the level on which we currently operate we use the following naming conventions. On the IRD schema level, we use the term metatype to denote any of the concepts used in a metamodeling language. On the IRD definition level, one of these metatypes is instantiated to describe a certain method component, resulting in what we call a type (i.e. an instance in a metamodel). Hence, in ME, an entity object type refers to an instance in a metamodel. This then itself plays the role of type on the ISD level, when it is instantiated to an entity used as an element in a model of the object IS.

Since some of the metamodeling constructs refer to instances of models, i.e. to the IRD level we need to refer to them also. For example, to refer to all entities described in an ER model we use the term instances of an entity object type. Because the naming becomes complicated we use apostrophes to refer to things on the IRD definition level. Hence ‘entity’ means the type described in a metamodel. This means the same as an entity object type although the latter is more precise, since it mentions also the metatype. Because in most cases the metatype is clear, e.g. it is clear that ‘class’ is an object type not a relationship type, we normally use the shorter naming version.

Starting from Teichroew et al. (1980), most of the meta-data modeling languages rely on some existing semantic data model (Hull and King 1987). Two types of semantic models, ER-based models and NIAM-based models, have been investigated in particular. Extensions of the ER model (Sorenson et al. 1988, Welke 1988, Smolander 1991, Venable 1993) seek to improve its expressive power by suggesting new integrity constraints (Welke 1988, Smolander 1991, Kelly and Tahvanainen 1994) and verification rules (Wijers 1991), and by representing complex objects (Venable 1993). The NIAM-based conceptual metamodeling formalisms (Bommel et al. 1991, Hofstede et al. 1993, Hofstede and Weide 1993) pursue similar goals, but are often founded on a more formal basis than the ER-based modeling languages.

The reasons for applying semantic data models in ME are the same as in ISD. They are easy to use, support communication, and yet are powerful and formal enough to describe methods and implement them in customizable ISD tools. Moreover, methods in CASE tools are largely based on semantic data models and thus their users are familiar with them. Some models, like ER or NIAM, are even applied at both levels. Because of the symmetry between models in ME and ISD the semantic data model based metamodels should be easy to use and understand for method users. This is especially relevant for incremental ME in which metamodels are constantly used to refine ISD methods. The requirement for ease of use is further highlighted if the users of the modeling tool or their customizers are not familiar with a specific programming language.

Second, support for communication is especially important when multiple method stakeholders need to agree on and participate in ME. Also, metamodels can be applied for teaching (Mathiassen et al. 1996) and method related helps can be generated from metamodels (e.g. MetaCase 1994). Support for easy use and communication are achieved by the use of graphical representation in metamodeling languages. Although some metamodeling languages seek to model methods totally with graphical constructs (e.g. CoCoA (Venable 1993)), in practice they all include some graphically “invisible” metamodeling constructs. In other words, not all constructs of the metamodeling language have notational support. Most of the approaches aim to add extra constraints (Smolander 1992, Ebert et al. 1996), or whole constraint languages (e.g. ter Hofstede 1993) to existing graphical metamodeling languages. Another approach is to apply graphical metamodeling languages to describe only a subset of the metamodeling constraints (e.g. Harmsen 1997).

From the method user point of view, easiness and support for communication could be better achieved with a natural language, rich pictures, or with other similar techniques, but they would not satisfy the third requirement of formality. Moreover, these do not reflect any knowledge specific to ME and metamethods: they do not explicitly describe or implicitly provide guidance on which components, rules, or constraints of methods should be considered during ME. In addition to pure representation of methods, metamodeling languages should provide a formal basis for building tool support. This means that all essential method knowledge must be captured into the formal metamodel.

The modeling power and formality of metamodeling can also be supported by other types of metamodeling languages. For example, for this purpose Saeki and Wenyin (1994) adapted an object-oriented modeling language called Object-Z. Ahituv (1987) introduces a formal metamodel which views an information system as the data flow that moves from one state to another, and by which some existing methods can be modeled. The work of (Oei et al. 1992, Oei and Falkenberg 1994, Oei 1995) introduces a formal language for modeling methods and transforming them into a method hierarchy. Also set-theoretical constructs (Bergsten et al. 1989), and predicate-logic (Brinkkemper 1996, Harmsen 1997) have been applied to metamodeling. However, these fail in other criteria as they neither support communication nor are they as easy to use as semantic data models (although some of them like MEL have close connections with the data modeling side). Semantic data models provide better modularity and maintainability, which are particularly important for incremental ME. Moreover, the development of metamodeling languages mainly to satisfy the modeling power aspect is questionable because this requirement can already be supported with programming languages. Hence, if we concentrate only on achieving the greatest possible modeling power, assembler or C++ is close to the ultimate metamodeling language.

The requirements formulated above are important for incremental ME and direct us to focus on semantic data models. Additional reasons for this focus are the popularity of semantic data models as repository schemas (CASE Outlook 1989), and the dominance of their use in large metamodeling efforts (Hong et al. 1993, Heym 1993, Henderson-Sellers and Bulthuis 1996a, 1996b, Hillegersberg 1997) when compared to other types of metamodeling languages. The former reason allows us to test and validate the metamodels in a tool environment (cf. Section 4.2.3), and the latter reason to compare the metamodels.

Like other modeling languages, metamodeling languages focus on specific aspects of the domain to be modeled, and therefore lead to different types of representations. One major difference between these languages is therefore how well they describe various types of method knowledge. This is related to our first research question, since our aim is to improve the metamodeling power of semantic data models. Ideally, a metamodeling language should capture method knowledge as completely as possible (Griethuysen 1982, Welke 1988, Brinkkemper 1990, Tolvanen et al. 1993). By complete we mean the 100% principle suggested by Griethuysen (1982) in the context of metamodeling, and Welke’s (1988) “no loss” criterion in the context of a repository metamodel.

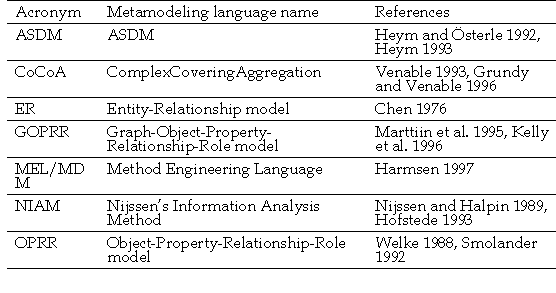
In the following we consider a small example to illustrate the use of different semantic data models in metamodeling. This allows us to describe different approaches to define method knowledge and to introduce them for later evaluation (cf. Section 4.5). We focus mostly on widely-known metamodeling languages. These are summarized in Table 3-3 and illustrated in the following subsections together with an example. The metamodeling languages mostly follow ER-based models, except NIAM which can be considered as an object-relationship model (Kim and March 1995), and MEL which is based on first-order predicate logic, but uses an ER-based graphical notation.

TABLE 3-3 Examples of metamodeling languages.

This example deals mainly with knowledge related to a single modeling technique, but also includes a connection to class diagrams. The example is quite common in object-oriented methods (e.g. Coad and Yourdon 1991a, Rumbaugh et al. 1991) but is made more explicit than is often possible to find from method text-books.

The metamodels made were reviewed by the users or developers of metamodeling languages, except the metamodel made with ASDM and MEL. Users of these metamodeling languages were not available, and their developers did not respond to our inquiries.

The ER model has been commonly applied as a schema for repositories (CASE Outlook 1989), and most of the meta-data modeling languages originate from the ER model. Therefore, several versions and dialects of ER modeling exist. They vary based on whether attributes are allowed only for entities, whether inheritance of entities is allowed, etc. (cf. Batani et al. 1992). Here we apply a version of the ER model which allows the definition of attributes attached to entities, and recognize cardinality constraints between entities (in an ER model this constraint defines how many times instances of an entity can participate in a relationship).

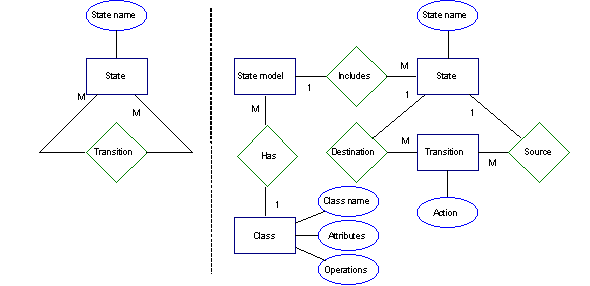
The reasons for extending the ER model for metamodeling are the same as in extending it for IS modeling - its limited modeling power. Figure 3-5 illustrates limitations of the ER model with two versions of our state model example.

 

FIGURE 3-5 Two metamodels of state model defined with the ER model.

In the figure, entities are illustrated with a rectangle, relationships with a diamond, and attributes with an ellipse. The cardinality constraints (1 or M in the metamodel) are shown side-by-side with the related entity. The metamodel on the left defines that each state can participate in several transition relationships, and that states have state names. No information is given for example on the state model itself, nor that transitions must be specified with an action.

To specify all rules in the example, the metamodel could be defined differently. For example, to specify that transitions are defined with an action, a transition could be defined as an entity instead of a relationship. The larger metamodel on the right illustrates this possibility. The cardinality constraint value one defines furthermore, that a transition can not be an n-ary relationship. However, when an entity type is used to represent a transition no distinction can be made between design elements that can exist independently (i.e. states) and design elements which exist between independent design elements (i.e. transitions). Thus, in the latter version of the metamodel, there is no explicit constraint (cf. Brodie 1984) to distinguish between transitions and states. Moreover, the metamodel does not specify method knowledge adequately because it allows transitions which are “unconnected” to states. This distinction between states and transitions could be made with the first version of the metamodel since in the ER model relationships can exist only when related to entities. This constraint is thus inherent in the ER model (a basic semantic property of the ER model, Brodie 1984). Moreover, other method knowledge related to state modeling with object-oriented methods is not defined adequately in either of the versions. For example, mandatory action names, unique state names, and the requirement that every class must be specified with state models are not captured with the ER model.

ASDM is a semantic data model developed at the University of St. Gallen and it has been used to describe the reference model of ISD (Heym and Österle 1992, Heym 1993). ASDM has also been used for metamodeling according to the rules defined in the reference model (Heym 1993). The reference model includes the widest range of method knowledge as it aims to cover other knowledge in addition to that defined in modeling techniques (part of deliverable model of the reference model). These extensions, excluded here, deal with the ISD process, versioning of metamodels, guidelines for integrity, and method related contingencies. Each of these is also represented with different metamodeling languages. Based on the reference model another, existing, metaCASE tool was used to develop a tool called MERET (Heym and Österle 1993), which could represent and compare methods, but not implement them into a CASE tool.

ASDM is used as a notation to metamodel modeling techniques (cf. Heym and Österle 1992). The notation of the language follows the ER model and initially Chen’s (1976) version of ER model was used to define methods. The extensions in ASDM deal with inheritance, aggregation and identifying different concepts in the modeling techniques. These concepts are subtyped from an entity type. Because of these extensions, our state model example can be specified more adequately than with the standard ER model (cf. Figure 3-6).

FIGURE 3-6 A metamodel of a state model defined with ASDM (adapted from Heym 1993, p 210).

Although the same entity symbol of ASDM is applied for most of the method concepts, the reference model classifies them into meta-entity types, meta-relationship types and meta-attribute types. Hence, a ‘transition’ is considered as a relationship type and an action as an attribute type. Furthermore, meta entity types are subtyped into fundamental entity types (i.e. state) and structural entity types (class name) although this can not be easily noticed from the graphical metamodel. Typically, structural entity types are results of an aggregation relationship.

The metamodel based on the reference model shares some of the limitations already discussed for the ER model. Links between modeling techniques are not defined, uniqueness of state names is not defined, and because minimum cardinalities can not be specified we can not define mandatory relationships. Although the reference model distinguishes techniques and their components, the “explains” (Heym and Österle 1992, p 11) relationship does not allow the definition of any rules of the technique-related connections other than the maximum cardinality. Hence, for example, the rule that each class must be specified in one or more state models can not be included in the metamodel. Moreover, the metamodels developed in Heym (1993) do not include these types of connections. The focus of the reference model, as reflected in its name, is on more general method knowledge and therefore it lacks detailed metamodeling capabilities. In fact, Heym and Österle (1993) aim to describe all method related knowledge at a high level of granularity to understand and compare methods.

The OPRR model has been developed by Welke (1988) and Smolander (1992). The focus of the OPRR model has been from the beginning to specify single modeling techniques. It extends the largely unspecified ‘role’ concept of the ER model to clarify the way in which objects participate in a certain relationship. In other words, the role defines what “part” an object plays in a relationship (Smolander 1992). A role can have also properties. OPRR applies the same representation as the ER model and the role type is represented by a circle.

This model forms a specification language for graphical method representations in the MetaEdit tool (Smolander et al. 1991). MetaEdit can be applied as a CASE tool (MetaCase 1994), metaCASE tool (Smolander et al. 1991), or even to customize other metaCASE tools (Rossi et al. 1992). To better address tool implementation and formalization of OPRR Smolander (1992) has added additional constraints into OPRR, namely identifying properties, a duplication policy for object types (whether homonyms are allowed), direction for relationships and modeling technique related data types. A useful feature of MetaEdit is that a graphical OPRR representation can be built up, and compiled in this environment at any time during metamodeling. Therefore the implementation of the CASE tool is easy and straightforward after the graphical representation of the method in OPRR has been achieved (see Tolvanen and Lyytinen 1993). This possibility allows testing the metamodel (cf. Figure 3-7) as a “specification” for IS modeling.

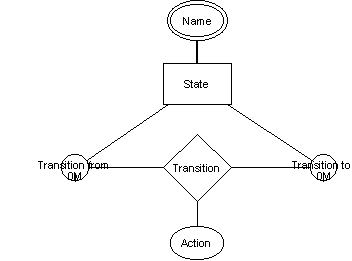
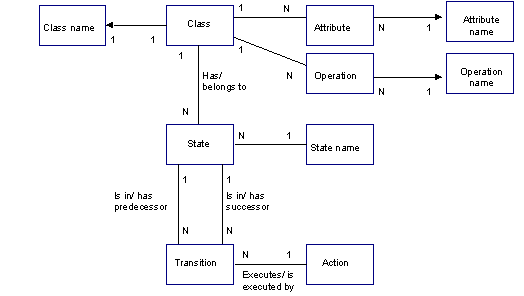
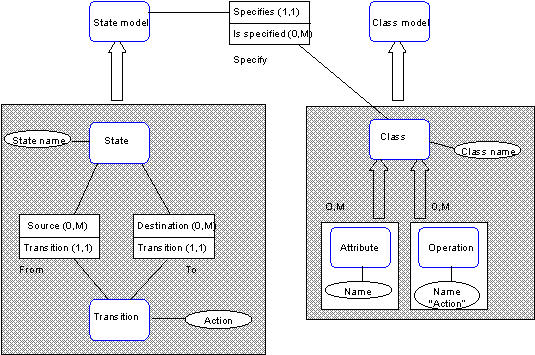
FIGURE 3-7 A metamodel of a state model defined with OPRR.

Regarding extensions to the ER model, the transition now has an action, and states are identified based on their names (double lined ellipse). The duplication policy is also used for states (although not represented in the graphical notation of OPRR): there can not be two different states with the same name. In modeling this means that copies of the same state are allowed, and changing the name of one state is reflected in all copies of that state. The uniqueness of states would make better sense if a state had other properties, like actions executed in the state (as in OMT, Rumbaugh et al. 1991).

Because OPRR focuses on specifying single techniques, a connection between a class and a state model can not be specified. Of course, the relationship could be specified with a normal OPRR relationship (like with the second version of the ER-based metamodel) but no distinction could be made between relationships between techniques and within a technique. Moreover, mandatory actions can not be specified, nor actions referring to operations of a class, nor that state names are dependent on the class they belong to. Thus, according to the OPRR metamodel a state model of another class can not use the same names for states (referring to different states).

MEL is a language for describing and manipulating (i.e. selecting and assembling) parts of ISD methods. It is designed specifically to support ME (Brinkkemper 1996, Harmsen 1997). Because of its general focus on supporting all ME tasks, MEL describes both product (i.e. conceptual structure and notation) and process aspects of method knowledge. In this sense it is very similar to ASDM (Heym 1993) although MEL has not been applied so extensively to model ISD methods. Like ASDM MEL too has a supporting tool, called Decamerone, for describing methods and customizing a third-party repository (Maestro II). The selected repository, however, limits the number of possible methods supported. Therefore Decamerone is limited to combining existing methods which can be already stored with Maestro II (e.g. the support for object-oriented concepts has only later been added into Maestro II).

Although MEL is founded on first order predicate logic, its relation to semantic data models can be easily detected. Moreover, MEL also includes a graphical modeling language which is a subset of MEL and very similar to the ER and OPRR models. Figure 3-8 illustrates the metamodel of our example, both with a textual and a graphical part of MEL. Parts of the metamodel which are related to guiding the method selection and modeling process are excluded.

 

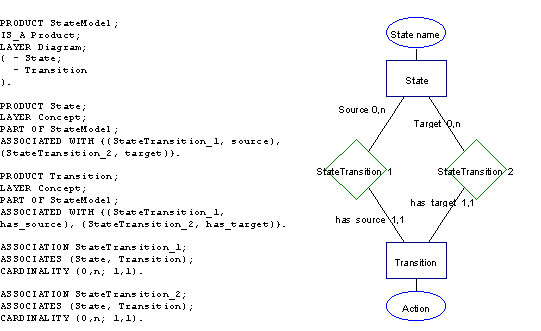
FIGURE 3-8 A metamodel of state model defined with textual and graphical part of MEL.

As the metamodels illustrate the textual and graphical part are largely equivalent. Since the graphical part is only a subset of MEL it is not adequate to define all the method knowledge of our example. The limitations are similar to the limitations of OPRR. In MEL additional constraints can be specified with predicate logic. For example, the following constraint to deny recursion could be added to a transition relationship:

These types of additions are possible for all metamodeling languages, but they provide limited help for method modeling since they do not guide towards modeling relevant aspects of methods. In other words, aspects which are not required in ME at all can be defined as well. This is paradoxical because the aim of methods is to focus attention on relevant aspects of IS, but on the metalevel (i.e. metamethods) this requirement is often ignored. Moreover, as already discussed, these extensions do not support maintainability, ease of use and communication as well as semantic data models.

By inspecting the definition of MEL and example metamodels it is unclear how all method knowledge related to the example can be specified with the predicate logic extensions. These include identity and different scopes: for example that each state must have a unique name among states of the class, and that actions must refer to operations defined for the related class. Unfortunately, the metamodels made to illustrate the use of MEL include only a few examples of detailed metamodels of modeling techniques.

CoCoA (ComplexCoveringAggregation) has been developed to support conceptualization and data modeling of complex problem domains (Venable 1993). As stated in the name of the model, its extensions deal with modeling aggregations which cover entities and named relationships, n-ary relationships, alias naming, and entity categories (through the named roles they participate in). CoCoA has also been applied in metamodeling (Venable 1993) and method integration, and is intended to be used as a metametamodel for a modeling tool (Grundy and Venable 1996). Most of the metamodeling efforts carried out with CoCoA have focused, however, on data modeling techniques, and larger metamodeling efforts including whole methods have not, to our knowledge, been reported.

Since method knowledge can also be considered as a complex object, i.e. as involving shared method elements and multiple levels of granularity, CoCoA performs better than the earlier metamodeling languages (cf. Figure 3-9). The metamodel specifies most of the method knowledge, such as identification of modeling techniques and their components: that more than one state model for a class is possible; and that transition relationships are binary. Furthermore, a covering aggregation is used to describe the components of the modeling technique (large gray box), and that a class can have several attributes and operations. Moreover, an “action” alias is used to denote that class operations are applied in transitions. This means that actions which are not described as operations should not be possible. However, the dependency to operations of a state model related class (or its superclasses) can not be specified.

 

FIGURE 3-9 A metamodel of a state model defined with CoCoA.

All method knowledge related to our example, however, is not specified even with CoCoA. First, no possibility exists to define which attribute values are mandatory: it should not be possible to define states without state names, or transitions without actions, but the CoCoA metamodel does not distinguish between mandatory and optional values. One possibility would be to model mandatory properties with a single aggregate, like an attribute of a class, with multiplicity value of one-to-one (1,1). Second, as in the ER model, the distinction between a transition and a state is not clear since they are not sub-typed as in ASDM (Heym 1993). However, with a minimum cardinality the mandatory participation of each transition in both possible roles is guaranteed. The difficulty to distinguish types which refer to a modeling technique (e.g. state model) and its components (e.g. state) also exists because both are represented as entities. Moreover, if the state model applied n-ary roles, the number of role instances a relationship instance can or must have can not be specified with CoCoA. Third, there is no specification of the requirement that a class can not have several different states with the same name. Implicitly, we can expect that each name must be unique, but CoCoA does not restrict the scope of instances in which the uniqueness should be valid. For example, along all class diagrams, classes with the same name typically denote the same class (e.g. Booch 1991), but several classes can have states named similarly but which still refer to different states.

NIAM (Nijssen’s Information Analysis Method) has been developed primarily to support information analysis (Verheijen and Van Bekkum 1982, Nijssen and Halpin 1989) but it has also been applied in several metamodeling efforts (e.g. Wijers 1991, Hofstede 1993). It is also a good example of method evolution since several versions of NIAM exist with a wide variety in the terminology. In the metamodeling effort we have applied basic NIAM with the PSM extension (Hofstede 1993). To our knowledge, no modeling tool using NIAM as a metametamodel is available.

The NIAM/PSM based metamodel of the state model example is illustrated in Figure 3-10. A state, a transition, a class, an attribute and an operation are defined as object types and illustrated with circles. As with the ER model, NIAM does not distinguish between relationships and objects. Although transitions could be modeled as a relationship, the constraints could not be specified as it is defined with an object type. Attributes, also called label types (ter Hofstede 1993) or slots (Verheijen and Van Bekkum 1982) are similarly represented with circles but the name of an attribute is described in brackets.

 

FIGURE 3-10 A metamodel of a state model defined with NIAM.

The linkages between attributes and object types are described with relationships (also called a bridge type or a fact type) although one-to-one relationships (e.g. between a class and a class name) could also be defined by adding the attribute name in brackets below the name of the object type. The use of relationships has the advantage of illustrating different constraints. A total role constraint, illustrated as a black dot on the object or attribute type part of the relationships, specifies a mandatory role. For example, each state must be described with a state name and all state names must belong to at least one state. The uniqueness constraint, illustrated with arrows in role symbols, shows which instances of a role or concatenation of roles must be unique. For example, only one instance of a class name can appear in the relationship between classes and class names. The uniqueness constraint is also used to define that each state can have only one state name, and the same state name can be used as a value for many states. The rule of the example that a class may have only one state with a given name could be added to the metamodel as a relationship with a uniqueness constraint, but then no difference could be made between different kinds of relationships (i.e. those defined between states and transitions of STD and those defined for describing constraints). The total role constraints in input and output roles define that each state has an input or an output of a transition and that each transition has a state as an input or output. This specification can not be used as a metamodel for guiding modeling actively. According to the constraints, creation of the first state would require creation of a transition which could not be possible because other states are not available.

Although NIAM can support most constraints of a state model it does not address multiple interconnected techniques. Therefore, the metamodel includes PSM extensions (ter Hofstede 1993). Modeling techniques are defined as schema types and illustrated as rounded boxes around technique related types. The linkage between state models and classes is described as a NIAM relationship. This relationship can be distinguished from other relationships because it is drawn outside the schema types. The total role constraint and the uniqueness constraint are used to define that each state model must be related to only one class (i.e. other classes can not refer to the same state model). Finally, linkages between the values of actions and operation names can not be defined with the graphical constraints of PSM/NIAM. As with MEL, additional grammars like LISA-D (Hofstede et al. 1993) have been proposed and could be used. For example, a correspondence between an operation name of a class and an action of a transition would then be:

 

GOPRR (Graph-Object-Property-Relationship-Role) has been developed from the OPRR data model (c.f. Smolander 1991, Marttiin et al. 1995, Tolvanen et al. 1993, Kelly et al. 1996, Kelly 1997). It has been developed specifically for metamodeling. The GOPRR model is implemented in a MetaEdit+ metaCASE tool (Kelly 1997, MetaCASE 1996a) which enables GOPRR-based metamodels to be instantiated at any time in the same tool as a model.

We will apply GOPRR in method analysis and metamodeling in Chapter 4. Therefore, the GOPRR model is described in more detail in the appendix. Here we briefly define the main extensions to OPRR. As the extra G in the acronym indicates, the main extension is a graph metatype. It is a collection of all other GOPRR types (including the graph type) chunked together into a modeling technique. The GOPRR model also offers three semantic relationship types between graphs and other non-property types (i.e. object, relationship and role types): inclusion, decomposition, and explosion. Inclusion means that a graph may consist of instances of particular object types, relationship types and role types. Moreover, an object type in a graph type may be either decomposed or exploded into another graph.

In addition to the graph metatype, GOPRR extends OPRR with an abstraction mechanism to generalize and specialize non-properties. It applies single inheritance, where an ancestor can contain a number of descendants, but each descendant can have only one ancestor. Cartesian aggregation is defined so that non-property types can contain any number of property types; in the other direction, a property type can be shared by many non-property types. GOPRR also applies cardinality constraints in a different way than in OPRR. In GOPRR, cardinality defines a minimum and a maximum number of instances of a role type a relationship type instance may have. In other words, this defines whether relationships are binary, specific n-ary, or whether some roles are optional. Other additions of GOPRR include local names for properties and a collection data type[14]. These are described in the example and in the appendix.

Because of these extensions GOPRR can capture almost all the method knowledge related to our example. GOPRR does not have a standardized graphical notation (Kelly 1997). Rather, metamodels are specified through forms represented as windows in MetaEdit+ tool (e.g. Rossi and Tolvanen 1995). One main reason for this choice is the relatively large number of constraints which are not best represented with a graphical notation. If they were added to increase the picturability (cf. Venable 1993) it would make GOPRR-based metamodel representations inherently complex. Graphical notations have, however, been implemented for metamodel representations. Following Kelly and Tahvanainen (1994) and Hillegersberg (1997) we have defined a similar graphical notation to make metamodels readable and more comparable with notations of other metametamodels. This notation is used to illustrate the example metamodel in Figure 3-11.

In the GOPRR representation used, a technique is defined as a graph type represented with a window symbol. Inclusion is described by drawing components (i.e. types) inside the window symbol of a technique (i.e. graph type). The relationship between a property and a non-property includes the local name of the property in that non-property, whether it is unique there, and whether it is the identifying property. For example, a class name is defined as an identifier and is unique among all classes. These constraints are not added to the property type because GOPRR supports reusability of types and these constraints may be different in other places where the property type is used (Kelly 1997). The data type of operations of a class is ‘collection’, and this is illustrated with a double-lined ellipse. Hence, the metamodel specifies that each class can have a collection of operations and each operation can be defined through its name and return type. More generally, a property type can also be linked to GOPRR types other than an object type.

 

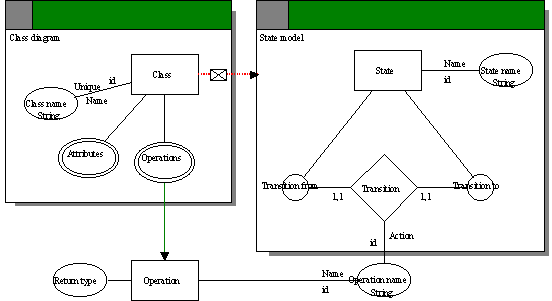
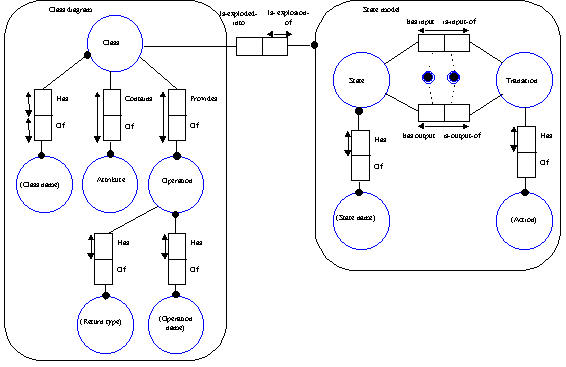
FIGURE 3-11 A metamodel of a state model defined with GOPRR.

Property sharing is used in the metamodel to define that both transitions and operations refer to the same operation name. For the purpose of state modeling, an operation is called an action by defining the local name. Modeling the life-cycle of classes with state models is specified with an explosion link represented as a dotted line with a cross in a box and an arrowhead from the class to the state model.

The GOPRR metamodel, however, does not define all method knowledge. Mandatory actions and state names can not be defined because the metamodel does not differentiate between optional and mandatory values. A recent addition to GOPRR for checking property values, however, can support the definition of mandatory properties. The uniqueness of state names depending on the class can not be specified because the uniqueness constraint is relevant among all instances (as with class names). Mandatory explosions (i.e. each class has at least one state model) and that only one class can refer to a single state model can not be specified. Moreover, although operation name and action refer to the same property type, similarly to the CoCoA alias, no restriction can be defined on the population of property type values. Hence, an action in a state model can refer to any operation defined for any class. The correct definition should be that an action can refer to any of the operations of the related class or its superclasses.

In this section we defined metamodeling in the context of ME and described a set of metamodeling languages. Our focus is on semantic data models because of their support for communication, ease of use, and a formal enough basis to enable metamodel-based tool adaptation.

The set of metamodeling languages is illustrated by modeling a small example of method knowledge. With respect to our first research question of representing method knowledge “completely”, the metamodeling exercises were used to analyze the modeling power of the metamodeling languages. This revealed both similarities and differences among the constructs provided for metamodeling, although the example was so small that not all limitations or strengths could be described. This would require modeling a larger sample of ISD methods, as performed in Chapter 4. The metamodeling exercises, however, clearly showed the limitations of the basic ER model and showed how additional constraints are used to model methods.

In this thesis our main interest is on finding essential metamodeling constructs which could be used as predefined and generalized (meta)knowledge about modeling techniques. In other words, constraints like cardinality in the ER model and explosions in GOPRR already guide engineers to identify, capture and construct certain aspects of method knowledge (i.e. for each relationship at least the maximum cardinality must be examined). The currently used constraints, however, are not adequate as the metamodeling example clearly demonstrates. Hence, instead of applying programming languages or additional grammars (e.g. Harmsen 1997, (ter Hofstede et al. 1993, Saeki and Wenyin 1994) we seek constructs which are relevant in metamodeling with semantic data models. The limited number of metamodeling constructs will help method engineers to focus on perceiving known rules about method knowledge, speed up the metamodeling process, and support communication among the participants in ME efforts. Hence, our aim is to find constructs specific to our domain of metamodeling, in the same way as developers of ISD methods try to find constructs specific to their domains of application.

[14] Recently GOPRR has been extended with multiplicity constraints, and with checking of property values through a constraint specification language (Kelly 1997).