PELITEORIAA
GAME THEORY
Päätöksenteon tukena käytettävä peliteoria muodostaa operaatiotutkimuksessa hyvin laajan osa-alueen, josta tässä käsitellään lähinnä vain kahden pelaajan pelejä ja niistäkin päällimmäisenä ko. pelityypin yksinkertaisin muoto, kahden hengen vakiosummapeliä. Verrattaessa peliteorian tehtäviä optimointitehtäviin on heti havaittavissa yksi olennainen ero: nyt tarkastellaan kahta tai useampaa päätöksentekijää joilla on toisilleen vastakkaiset etunäkökohdat.
Tarkastellaan kahden hengen vakiosummapelin erikoistapausta kahden hengen nollasummapeliä. Ensin muutamia käsitteitä. Pelaajia on luonnollisesti kaksi: rivipelaaja (row player) ja sarakepelaaja (column player). Näistä kummallakin on valittavanaan useita strategioita, esimerkiksi rivipelaajalla strategiat 1,..,m ja sarakepelaajalla 1,...,n. Kunkin strategian käyttö tuo suhteessa toisen pelaajan käyttämään strategiaan jonkin tuloksen, palkkion ja erityisesti nollasummapelissä näiden palkkioiden summa on nolla kaikilla strategioilla. Vakiosummapelin periaate on aivan sama mutta edellämainittu summa ei välttämättä ole nolla vaan on jokin vakio C. Palkkiot ja strategiat tavataan esittää ns. palkkiomatriisin (reward matrix) avulla.

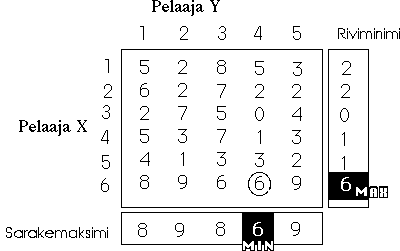
Nollasummaisuus tarkoittaa matriisissa sitä että palkkiot kuvaavat rivipelaajan voittoja ja sarakepelaaja häviää vastaavan summan. Kun kaikki arvot ovat positiivisia niin sarakepelaaja aina häviää enemmän tai vähemmän, mutta luvut ovat tietenkin suhteellisia ja esimerkkimatriisikin näyttää varmasti mielekkäämmältä mikäli jokaisesta palkkiosta vähennettäisiin vaikkapa 5. Vaihtoehtoinen tapa olisi esittää strategiat puumallilla. Yllä vasemmalla yksinkertainen nollasummapelin matriisi.
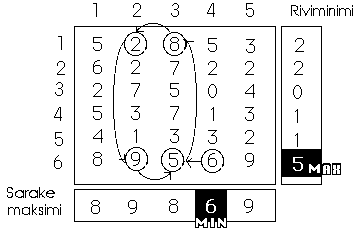
Pelin ratkaisutapa on yksinkertainen: haetaan jokaiselta riviltä riviminimi ja jokaiselta sarakkeelta sarakemaksimi. Sitten haetaan riviminimien maksimi ja vastaavasti sarakemaksimien minimi. Nämä tulokset antavat optimaalisen strategian kumpaisellekin pelaajalle. Ei siis pelata uhkapeliä vaan valitaan se vaihtoehto jossa on paras huono tulos. Perusoletus pelissä on että pelataan aina parhaalla mahdollisella tavalla ja vastustaja tuntee tämän strategian. Tässä esimerkissä siis pelaaja X valitsee strategian 6 ja pelaaja Y strategian 4. Mikäli on voimassa Min{Sarakemaksimi} = Max{Riviminimi} niin pelillä sanotaan olevan satulapiste (saddle point) ja satulapisteessä on pelin arvo rivipelaajalle. Jos satulapistettä ei ole niin pelin arvoa ei voi laskea. Yllä olevassa esimerkissä on satulapiste sillä Min{8,9,8,6,9} = 6 = Max{2,2,0,1,1,6}.
Mikäli pienennetään X:n palkkiota pisteessä (X,Y) = (strat. 6, strat.3) yhdellä eli 5:ksi (oikeanpuoleinen kuva) niin tilanne muuttuu sikäli että kumpikin pelaaja valitsee edelleen samat strategiat, mutta pelistä katoaa satulapiste. Eli Min{8,9,8,6,9} = 6 ≠ 5 = Max{2,2,0,1,1,5}. Tällaisessa tilanteessa voitaisiin lähteä myös spekuloimaan kuinka pelaajat käyttäytyisivät jos arvaisivat minkä strategian toinen valitsee. Tällainen "ketjuarvailu" ("jos X tietää Y:n tietävän ...)" asettuu kuitenkin jo muutaman askeleen jälkeen luuppiin, jonka ulkopuolelle jääviä strategioita ei kumpainenkaan pelaaja valitsisi. Tällainen tilanne, jossa kahden hengen nollasummapelillä ei ole satulapistettä, ratkaistaan eliminoimalla ensin ns. dominoivia strategioita ja lopuksi ratkaisemalla tehtävä joko graafisesti tai LP-ongelmana.
On myös sen luonteisia pelejä, joissa ei ole mahdollista löytää sen enempää sarakemaksimin minimiä kuin riviminimin maksimiakaan koska kumpiakin on useita kappaleita. Tyypillinen esimerkki tällaisesta pelistä on lasten suosima ns. Kivi-paperi-sakset-peli, jossa pelaajat pitävät käsiään piilossa selän takana ja tuovat ne sitten näkyville täsmälleen yhtäaikaa. Kummallakin pelaajalla on valittavanaan kolme strategiaa, jotka esitetään käden asennolla (paperi: kämmen auki, sakset: kaksi sormea ojossa, kivi: käsi nyrkissä). Palkkiomatriisi saadaan muodostettua kun tiedetään että "kivi rikkoo sakset, joka leikkaa paperin, joka voi kääriä sisäänsä kiven". Tämän seurauksena palkkiomatriisi näyttää seuraavanlaiselta:
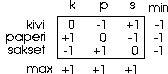
Tehtävä voidaan ratkaista LP-ongelmana, jolloin jokainen strategia saa painoarvon 1/3. Pelin arvoksi saadaan nolla.
Kahden hengen ei-vakiosummapelit voidaan jakaa ns. yhteistoiminnallisiin (cooperative) ja ei-yhteistoiminnallisiin (non-cooperative) peleihin. Tarkastellaan esimerkkinä pientä ei-yhteistoiminnallista peliä eli peliä jossa pelaajat eivät saa suunnitella strategiaansa yhdessä sekä mitä tapahtuu kun pelistä tulee yhteistoiminnallinen. Palkkiomatriisi poikkeaa nollasummapelin palkkiomatriisista s.e. valittujen strategioiden tuottamat palkkiot ilmoitetaan lukuparina (x,y), missä vasemmanpuoleinen luku antaa rivipelaajan palkkion ja oikeanpuoleinen sarakepelaajan palkkion. Koska annetut luvut ovat nyt voittoja molemmille pelaajille niin sen seurauksena lasketaan myös sarakepelaajalle maksimipalkkio minimipalkkioiden joukosta eikä päinvastoin. Esimerkki valaisee asiaa. Seuraavassa hieman "humoristinen" esimerkki, jossa on jo ajan patinaa minkä vuoksi pieni epäolennainen lisäselitys lienee paikallaan. Esimerkki on tehty 90-luvun alussa, jolloin Venäjän parlamentti Ruslan Haslubatovin johdolla oli napit vastakkain presidentti Boris Jeltsinin kanssa. "Venonen" on viittaus suomalaisten hyvin tuntemaan Terho Pursiaiseen ja "ruusulainen" taas viittaa "Russia" ja "Ruotsi" sanojen erääseen otaksuttuun yhteiseen alkuperään (Roslagen).
Esimerkki (vuodelta 1992...). Yliopiston johtamiskoulutuksen Strategiaklubin vieraana on futurologi Teo Venonen. Venonen pureutuu esitelmässään kansainvälisen konfliktintutkimuksen ongelmiin peliteorian mallien avituksella. Jotta sihti tulevaisuuteen olisi kohdallaan täytyy kunnon futurologin tarkentaa suunta historiasta. Ja niin: "Keskustan valtakunnan, Kiinan, ja erään löylynlyömän länsimongolialaisen kansan välille perustivat Euroopasta tulleet siirtolaiset, venelaiset, tuhat vuotta sitten valkonaamojen imperiumin. Uuden valtakunnan asukkaita alkoivat svealaiset, joita länsimongolit kutsuivat ruusulaisiksi näiden kotimaakunnan, Roslagenin, mukaan, kutsua ruusulaisiksi Roslagenin oman maakuntansa mukaan. Niinpä noista ajoista saakka ovat kaikki muut kutsuneet venelaisia ruusulaisiksi paitsi länsimongolit, joiden mielestä svealaiset olivat ruusulaisia.Ruusuisesta historiasta päästään nykypäivään, josta ei voi sanoa samaa. Venelaisten maa natisee liitoksissaan kun kaksi kansanparantajaa kiistelee menettelytavoista. Boris J. haluaa parantaa maan taloudellista tilaa demokraattisin keinoin ja Ruslan H. parlamentaarisin menetelmin. Ja kuten usein kun ihmisistä on kyse, ylevien periaatteiden takana on kysymys myös vallasta ja niinpä miehistä kumpaisellakin on vain kaksi päästrategiaa:
Oman vallan lisääminen toisen kustannuksella (X) tai konsensus vastapuolen kanssa (Y). Kummankin strategian tuotto on arvioitu s.e. kaikkien (1°) valtaoikeuksien kahmiminen itselle antaa yhden pisteen ja vastaavasti menetys kaksi miinuspistettä (2°) valtakunnan hajoamisen keskeytyminen antaa nollan ja vastaavasti hajoaminen miinuksen. Näillä tiedoilla saadaan kvaltion hajoaminen).
Oikeanpuoleinen matriisi kuvaa tilannetta, jossa tshetseeni Ruslanin motiivit on arvioitu toisin. Eli jollei imperiumi voi laajentua uudelleen monikansalliseksi niin toiseksi paras vaihtoehto on Venäjän hajoaminen itsenäisiin osiin kuten Tshetsenia, Tatarstan, Pietari, Novgorod, Komi, Marimaa, Ural, jne... Hajoaminen antaa siis Ruslanille pluspisteen. Mielenkiintoista on havaita että edelleenkin pelaajat valitsevat samat strategiat vaikka lopputulos on Borikselle vieläkin huonompi"

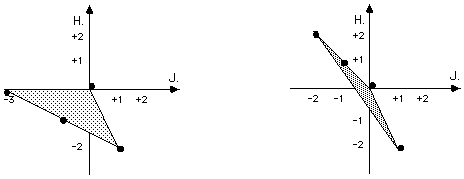
Venonen jatkaa: "Muutetaan peli nyt yhteistoiminnalliseksi eli pelaajat suunnittelevat yhdessä strategian, joka antaa kokonaisuuden kannalta edullisimman lopputuloksen. Nyt on selvää että vasemmanpuoleisessa pelitilanteessa pelaajat valitsevat strategian Y eli konsensuksen, joka johtaa status quo tilanteeseen (±0,±0) ... ainakin joksikin aikaa. Jälkimmäisessä tilanteessa (oik.puol. matriisi) Ruslanin suostuttelu yhteistoimintaan on jo vaikeampaa. Asetelmaa voidaan valaista piirtämällä tilanteista graafiset mallit (kuvat alla) s.e. kukin palkkiopari merkitään kaksiulotteiseen koordinaatistoon pisteenä kun koordinaattiakseleina toimivat rivi- ja sarakepelaajat. Sitten rajataan uloimpia pisteitä myöten konveksi monikulmio s.e. kaikki palkkiopisteet ovat joko kulmion reunalla tai sisällä. Neuvottelualue sijaitsee monikulmion koillisosassa, joka oikeanpuoleisessa kuvassa on perin kapea."
Paitsi matriiseina, voidaan peliteoreettisia ongelmia ratkoa myös päätöspuilla, lyhyesti voidaan kiteyttää, että päätöspuissa eri valinnoille annetaan todennäköisyydet eri puun haarautumiskohdissa. Päätöstä tehdessä lasketaan sitten yhteistodennäköisyydet.
Tällä kurssilla ei ole vielä toistaiseksi käsitelty usean pelaajan peliasetelmia. Kun pelaajia on useampia niin asetelmat tulevat huomattavasti monimutkaisemmiksi ja n-pelaajan asetelmat tarjoavatkin laajan tutkimusalueen, jossa kynnettävää sarkaa vielä riittää. Yksi tapa tutkia usean pelaajan asetelmia on simulointi ja tähän liittyy myös tämän kurssin pitäjän kiinnostus verkkoteorian tutkimustyön yhteydessä syntyneeseen kolmen pelaajan shakkiin ja sen laajennuksiin.