Jorma Kyppö

Hakemistoon

MATRIISILASKENNAN PERUSTEITA

m x n - matriisi A, joka sisältää m riviä ja n saraketta

a₁₁ a₁₂ a₁₃ . . . a_1n

a₂₁ a₂₂ a₂₃ . . . a_2n

. . . . . . . . . . .

a_m1 a_m2 a_m3 . . . a_mn

Erikoismatriiseja. Kyseessä on:

Neliömatriisi jos m=n. Neliömatriisin päälävistäjä eli päädiagonaali käsittää alkiot a_ij, joille i=j.

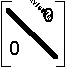
Nauhamatriisi (kuva) jos neliömatriisin keskelle muodostuu päälävistäjän suuntainen nauha, jonka ulkopuolelle jäävät alkiot ovat nollia.

Tridiagonaalimatriisi jos nauhamatriisin nauhan leveys on kolme. Käytetään monissa sovelluksissa.

Diagonaalimatriisi (lävistäjämatriisi) jos päälävistäjän alkioita lukuunottamatta kaikki alkiot ovat nollia eli a_ij = 0 jos i ¹ j. Diagonaalimatriisi on

siis nauhamatriisi, jonka leveys on yksi.

Yksikkömatriisi jos diagonaalimatriisin kaikki päälävistäjällä olevat alkiot ovat ykkösiä eli a_ij = 1, kun i = j ja a_ij = 0, kun i ¹ j. Yksikkömatriisista käytetään merkintää I.

Harva matriisi jos se sisältää runsaasti nolla-alkioita.

Matriisin A käänteismatriisi A^-1 jos pätee AA^-1= I.

Matriisi on säännöllinen jos sillä on käänteismatriisi. Jos matriisi ei ole säännöllinen niin sitä kutsutaan singulaariseksi.

Säännöllisen matriisin determinantti ei ole nolla eli det A ≠ 0. Esimerkki 3x3 matriisin determinantin laskemisesta sivun alalaidassa, 2x2 matriisissa lasketaan ainoastaan: a₁₁a₂₂ - a₂₁a₁₂, Huom! determinantti lasketaan toisin kun n>3).

- matriisin A transpoosi A^T kun A:n rivit ja sarakkeet on vaihdettu toisiinsa.

- nollamatriisi jos matriisin kaikki alkiot ovat nollia.

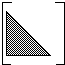
- alakolmiomatriisi jos a_ij = 0, kun i < j (kuva).

- yläkolmiomatriisi jos a_ij = 0, kun i > j (kuva).

- symmetrinen matriisi jos a_ij = a_ji " i,j.

- rivivektori jos m=1 eli matriisi on muotoa 1 x n.

- sarakevektori jos n=1 eli matriisi on muotoa m x 1.

Diagonaalimatriisi …….……... Yläkolmiomatriisi ………..….. Alakolmiomatriisi ………..….. Nauhamatriisi

…………..…………...... ………..………..….. ………….…..…..

Joitakin matriisien peruslaskutoimituksia:

Summa A+B: a_ij + b_ij" i,j ja erotus A-B: a_ij - b_ij " i,j.

Vakiolla kertominen cA: c*a_ij " i,j.

- Tulo C=AB: c_ij =S a_ik b_kj. Määritelty vain jos A:n sarakkeiden määrä on B:n rivien määrä. Tulomatriisi C on muotoa m x n kun A: m x p ja C: p x n. Yleensä AB≠BA. Ax on matriisin A ja vektorin x tulo kun A on m x n -matriisi ja x on n x 1 -vektori. x^Ty = Sx_iy_i on vaaka- ja pystyvektorien sisätulo eli skalaaritulo kun vektori x on muotoa 1 x n ja y muotoa n x 1. Sisätulon lopputulos on aina luku (esimerkki alempana).

- (A^T)^T =A, (A+B)^T=A^T+B^T ja (AB)^T=B^TA^T.

Esimerkki sisätulosta:

……..………1

[1, 2, 3] * 2 = 1*1+2*2+3*1= 8

……………..1

Esimerkki matriisin determinantin laskemisesta Sarrusin säännöllä. Sääntö toimii ainoastaan 3x3 -matriisilla:

……..1 ...0 ...2

A = 1 ...1… 1 … Þ … det A = (1*1*1+0*1*0+2*1*2) - (0*1*2+1*0*1+1*2*1) = (1+0+4) - (0+0+2) = 3

……..0... 2 ...1

Operaatiotutkimuksen ja matematiikan perusteet, Tietojenkäsittelytieteiden laitos, Informaatioteknologian tiedekunta, Jyväskylän yliopisto