ORM (TJT Y 30) kl. 99 6. DEMOT (viikko 9)

Operaatiotutkimuksen ja matematiikan perusteet

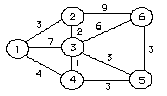
1. Määrää Dijkstran algoritmilla lyhin polku solmusta 1 solmuun 6 oheisesta verkosta:

2. Väinö on jälleen laajentanut bisneksiään ja valmistaa nyt neljää paitatyyppiä, kutakin eri paikkakunnalla: Tampere, Lahti, Vajaakylä ja Los Halpako. Paitatyyppien A, B, C ja D valmistuskustannukset paikkakunnittain ovat seuraavat:

A=(9,7,8,10), B=(8,7,7,5), C=(4,6,5,5), D=(3,4,5,2).

Miten paitojen valmistuksen tulisi jakautua paikkakunnittain, jotta kokonaiskustannukset saataisiin minimoitua kun paikkakuntia kuvataan vektorilla (T,L,V,H). Entä miten valmistuksen siirtäminen osittain ulkomaille vaikuttaa malliin?

3. Väinön yritys on sulautunut suureen kreikkalaiseen paitakonserniin, jonka johtaja Eijos Kallis on päättänyt laittaa firmansa eurokuntoon. Konserni valmistaa nyt m kpl erilaisia paitoja ja jokainen paita vaatii n:n koneen käyttöä. Merkitään koneita: M₁,..., M_n.

Yhden paidan i valmistamiseen koneella j kuluu t_ij tuntia (i=1..m ja j=1..n). Kone M_j on käytössä korkeintaan T_j tuntia viikossa ja yksi tunti samassa koneessa maksaa g_j markkaa. Eijos tietää, että paidasta i saadaan c_i markkaa myynnissä. Laadi malli, jolla voidaan laskea kunkin paidan viikottain valmistettavat määrät, kun halutaan maksimoida kokonaishyöty.

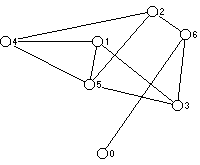
4. Selvitä (perustellen) oheisesta ja tehtävän 5 verkosta seuraavat asiat:

a) onko kyseessä tasoverkko ?

b) löytyykö verkosta siltaa ja/tai leikkaussolmua?

c) mikä on verkon suurin klikki?

d) montako väliä sisältää verkon komplementti?

e) Hamiltonin polku?

f) löytyykö tästä tehtävästä Väinöä?

5. Piirrä Suomen nykyisestä ja sitä edellisestä läänijaosta duaaliverkko.