1. Neljä firmaa, A, B, C ja D ovat keskittäneet toimintansa Hauhoon, josta on keskimäärin yhtä pitkä matka jokaisen suomalaisen luo. Eräänä päivänä kukin firma saa neljä tilausta eri puolilta Suomea, pohjoisesta, etelästä, lännestä ja idästä. Koska mikään firmoista ei voi hoitaa useita kuljetuksia saman päivän aikana niin tilaukset päätetään jakaa. Optimoi kuljetuskustannusten yhteissummaa kun kunkin firman kuljetuskustannukset eri ilmansuuntiin on ilmoitettu kustannusmatriisissa alla.

2. Jyväskylän kaupungin upouudella poliisilaitoksella on eräänä aamuna vapaana 7 rikostutkimusryhmää. Samoin aamulla on 7 rikosta selvitettävänä. Alla olevassa taulukossa on annettu keskimääräinen aika (työtunteina), mikä kultakin ryhmältä kuluu vastaavan tyyppisen rikoksen selvittämiseen. Ratkaise kuinka poliisipäällikön tulisi määrätä rikokset eri tutkimusryhmille, jotta selvitysaikojen summa olisi mahdollisimman pieni.

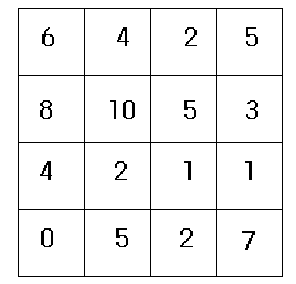
3. Suositussa TV-ohjelmassa Napanolla on jokaisessa ohjelmassa neljä naista ja miestä. Nämä vastaavat viiteen monivalintakysymykseen, joiden vastaukset pisteytetään. Sitten jokaisen vastaajan kunkin kysymyksen pisteet vähennetään jokaisen vastakkaisen sukupuolen edustajan vastaavasta pistemäärästä ja erotuksien itseisarvot summataan henkilöittäin. Kun kaikki ovat vastanneet lähetetään aineisto savolaiselle älykone Uatamille, joka tulostaa alla olevan matriisin. Mitä suurempi luku, sitä paremmin yhteen soppii. Hae unkarilaista menetelmää käyttäen jokaiselle daamille soveliain kavaljeeri tai halutessasi päinvastoin.

4. Agentti Cooper on saanut ratkaistavakseen L.P. -ongelman, murhan, joka on tehty Twin Peaksin kaupungissa. Vietettyään paikallisessa kuppilassa munkilla ja kahvilla höystetyn iltapäivän hän näkee seuraavana yönä kofeiininhuuruisen unen, josta saa idean kuinka seuloa viiden epäillyn miehen joukosta murhaaja. Syyllinen olisi mitä ilmeisemmin murhatun neiti L.P.:n viidestä poikaystävästä. Ongelma oli siinä, että L.P.:llä oli suhde jokaiseen näistä viidestä. Ja lisäksi jokaisella miehellä on suhde neljään muuhun neitoseen! Tehtävänä on näin ollen selvittää kuka on kenenkin todellinen poika/tyttöystävä. Kriteerinä käytetään keskinäisten riitojen määrää. Siis mitä vähemmän keskinäisiä riitoja on niin sitä todennäköisempää on suhteen vakavuus. Tarkastelun lopussa tulee jokaisella epäillyistä murhaajakandidaateista olla ainoastaan yksi tyttöystävä ja riitojen yhteismäärä mahdollisimman pieni. Varmuudella todennettujen riitojen määrät näkyvät alla. Kuka herroista on mahdollisesti syyllinen?