Au­to­maat­ti ja kie­li­op­pi

Tent­tiin 6.11.2019 pe­rus­tu­va it­se­opis­ke­lu­si­vu

Tä­män vep­pi­si­vun avul­la voit har­joi­tel­la kurs­sin TIEA241 Au­to­maa­tit ja kie­li­opit tent­te­jä var­ten. Si­vul­la esi­te­tään 6.11.2019 pi­de­tyn ten­tin ky­sy­myk­set ja vas­tauk­set, ja ker­ro­taan, mik­si oi­keat vas­tauk­set ovat sel­lai­set kuin ovat. Jot­ta voi­sit miet­tiä it­se en­nen kuin luet vas­tauk­sen, oi­keat vas­tauk­set ja muu­ta tie­toa on pii­los­sa rus­keis­sa alueis­sa. Ne tu­le­vat nä­ky­viin, kun siir­rät kur­so­rin niit­ten pääl­le. Ko­kei­le täs­tä!Toi­mii! (Jois­sa­kin iP­ho­neis­sa tä­mä ei toi­mi.)

Muu­ta­mis­sa koh­dis­sa on kent­tä, jo­hon voit syöt­tää oman vas­tauk­se­si. Vas­taus­nap­pi ”oi­keal­le” tuot­taa pa­laut­teen oi­keal­la ole­vaan laa­tik­koon. Yleen­sä on kä­te­vin­tä en­sin kli­ka­ta si­tä. Vas­taus­nap­pi ”uu­teen” tuot­taa pa­laut­teen uu­teen vä­li­leh­teen tai uu­teen ik­ku­naan riip­puen se­lai­me­si ase­tuk­sis­ta. Si­tä kan­nat­taa käyt­tää, jos ”oi­keal­le”-na­pin tuot­ta­ma pa­lau­te ei mah­du laa­tik­koon.

Ten­tis­sä vas­tat­tiin kon­sep­ti­pa­pe­ril­le. Mu­ka­na ei saa­nut ol­la kir­jo­ja, las­kin­ta tms. Jo­kai­nen teh­tä­vä oli ta­san 6 pis­teen ar­voi­nen. Pis­teet ja­kau­tui­vat ta­san ala­koh­tiin (a), (b) jne., pait­si mis­sä sa­not­tiin toi­sin. Pis­tey­tys ei ol­lut ”kaik­ki tai ei mi­tään” -pe­riaat­teel­la, vaan oi­kean­suun­tai­nen vas­taus tuot­ti osan pis­teis­tä, teh­tä­väs­tä riip­puen jo­pa nel­jäs­osa­pis­teit­täin.

Eri ten­teis­sä on tie­ten­kin eri ky­sy­myk­set. Ai­he­pii­rit ovat kui­ten­kin pal­jol­ti sa­mo­ja. Tä­män ten­tin vas­taus­ten ul­koa opet­te­lu ei to­den­nä­köi­ses­ti au­ta pal­joa tu­le­vis­sa ten­teis­sä. Vas­taus­ten ta­ka­na ole­vien pe­riaat­tei­den opet­te­lu niin, et­tä osaa so­vel­taa nii­tä eri­lai­sis­sa ti­lan­teis­sa, aut­taa to­den­nä­köi­ses­ti hy­vin pal­jon. Al­la ole­vien se­li­tys­ten ja esi­merk­kien ta­voit­tee­na on aut­taa ym­mär­tä­mään ne.

Kai­kis­sa ky­sy­myk­sis­sä ei pyy­det­ty pe­rus­te­le­maan vas­taus­ta. Sil­ti on hy­vä tie­tää, mik­si oi­kea vas­taus on se mi­kä se on. Sik­si ne­kin vas­tauk­set on pe­rus­tel­tu al­la.

Al­la ole­via ku­vaa ja kie­li­op­pia tar­vi­taan mo­nes­sa teh­tä­väs­sä. Saat ne pa­lau­te­laa­tik­koon sen al­la ole­vas­ta lin­kis­tä. Myö­hem­min täl­lä vep­pi­si­vul­la on ker­rot­tu, mis­tä ne ovat pe­räi­sin.

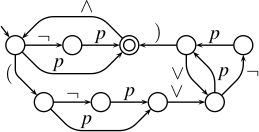C  ::=  L  |  (G)  |  C ∧ L  |  C ∧ (G)
D  ::=  B  |  D ∨ B
G  ::=  L ∨ L  |  G ∨ L
B  ::=  L  |  B ∧ L
L  ::=  p  |  ¬p

1. (a) On­ko ku­van au­to­maat­ti NFA? On­ko se DFA?

On­ko se NFA?Kyl­lä. pe­rus­te­luKu­vas­sa ei ole muu­ta kuin yk­sin- ja kak­sin­ker­tai­sia ym­py­röi­tä (epä­lop­pu­ti­lat ja lop­pu­ti­lat), ni­mel­lä va­rus­tet­tu­ja nuo­lia nii­den vä­lil­lä (kaa­ret) se­kä yk­si tyh­jäs­tä al­ka­va nuo­li, jo­ka osoit­taa al­ku­ti­lan. Aak­kos­to mää­räy­tyy ku­ten (b)-koh­das­sa.

On­ko se DFA?Kyl­lä. pe­rus­te­luSe on NFA, jon­ka mis­tään ti­las­ta ei läh­de ε-kaar­ta ei­kä kah­ta sa­man­ni­mis­tä kaar­ta. Jo­kai­nen sel­lai­nen NFA on DFA.

(b) Mi­kä on ku­van au­to­maa­tin aak­kos­to?

vas­taus{(, ), p, ¬, ∧, ∨} pe­rus­te­luKos­ka aak­kos­toa ei ole erik­seen il­moi­tet­tu, käy­te­tään yleis­sään­töä eli ke­rä­tään kaar­ten var­rel­ta muut mer­kit kuin ε. Tu­los il­moi­te­taan jouk­ko­na, kos­ka aak­kos­to on jouk­ko.

(c) Kir­joi­ta mah­dol­li­sim­man ly­hyt merk­ki­jo­no, jon­ka ku­van au­to­maat­ti hyl­kää.

vas­tausε

Mik­si ku­van au­to­maat­ti hyl­kää tä­män merk­ki­jo­non? vas­tausε tar­koit­taa tyh­jää merk­ki­jo­noa. Al­ku­ti­las­ta ei pää­se ε-kaa­ril­la mi­hin­kään lop­pu­ti­laan, kos­ka al­ku­ti­la ei it­se ole lop­pu­ti­la ei­kä sii­tä läh­de ε-kaa­ria. Sik­si au­to­maat­ti hyl­kää tyh­jän merk­ki­jo­non.

Mik­si tä­mä merk­ki­jo­no on mah­dol­li­sim­man ly­hyt? vas­tausMi­kään merk­ki­jo­no ei ole ly­hyem­pi kuin ε. Au­to­maat­ti ei hyl­kää mi­tään ε:a ly­hyem­pää merk­ki­jo­noa, kos­ka sel­lai­sia ei ole ole­mas­sa­kaan.

(d) Kir­joi­ta mah­dol­li­sim­man pit­kä merk­ki­jo­no, jos­sa ∧ esiin­tyy kor­kein­taan ker­ran, ∨ esiin­tyy kor­kein­taan ker­ran, ja jon­ka ku­van au­to­maat­ti hy­väk­syy.

Oi­kei­ta vas­tauk­sia on kak­si: tä­mä(¬p∨¬p)∧¬p ja tä­mä¬p∧(¬p∨¬p). Vas­tauk­sek­si kel­paa niis­tä kum­pi ta­han­sa.

Pe­rus­te­lu al­kaaAl­ku­ti­las­ta kan­nat­taa läh­teä jo­ko ¬:lla tai (:lla, kos­ka p vie sa­maan kuin ¬p mut­ta vä­hem­mil­lä mer­keil­lä. Jos läh­de­tään ¬:lla, niin seu­raa­va­na on p ja ol­laan lop­pu­ti­las­sa. Jos läh­de­tään (:lla, niin kan­nat­taa va­li­ta (¬p∨¬p, kos­ka se on pa­rem­pi kuin toi­sen tai mo­lem­pien ¬ ohit­ta­mi­nen, ei­kä mui­ta vaih­toeh­to­ja ole. Sen jäl­keen ei voi­da va­li­ta ∨, kos­ka ∨ on jo käy­tet­ty. On pak­ko va­li­ta ), jo­ka vie lop­pu­ti­laan. ja jat­kuuLop­pu­ti­las­ta voi­daan jat­kaa ∧:lla al­ku­ti­laan ja sen jäl­keen ede­tä uu­del­leen al­ku­ti­las­ta lop­pu­ti­laan, mut­ta vain yh­den ker­ran, kos­ka ∧ saa esiin­tyä enin­tään yh­den ker­ran. Saa­daan nel­jä yh­dis­tel­mää ¬p∧¬p, ¬p∧(¬p∨¬p), (¬p∨¬p)∧¬p ja (¬p∨¬p)∧(¬p∨¬p). Niis­tä vii­mei­nen ei kel­paa, kos­ka sii­nä on kak­si ∨:ta. Kes­kim­mäi­set kak­si kel­paa­vat ja ovat yh­tä pit­kät. En­sim­mäi­nen on nii­tä ly­hyem­pi, jo­ten se ei ole mah­dol­li­sim­man pit­kä..

(e) Luet­te­le kaik­ki sel­lai­set luon­nol­li­set lu­vut, et­tä ku­van au­to­maat­ti ei hy­väk­sy yh­tään sen pi­tuis­ta merk­ki­jo­noa. Pe­rus­te­le vas­tauk­se­si.

vas­taus0

Mai­ni­tut lu­vut kuu­luu lue­tel­la täs­tä syys­täAu­to­maat­ti ei hy­väk­sy yh­tään nol­lan pi­tuis­ta merk­ki­jo­noa, kos­ka ai­noa sen pi­tui­nen merk­ki­jo­no on ε, ja (c)-koh­das­sa näh­tiin, et­tä au­to­maat­ti hyl­kää sen..

Muut lu­vut kuu­luu jät­tää pois luet­te­los­ta täs­tä syys­täAl­ku­ti­las­ta pää­see lop­pu­ti­laan p-kaar­ta pit­kin, jo­ten au­to­maat­ti hy­väk­syy 1:n pi­tui­sen merk­ki­jo­non p. Al­ku­ti­las­ta pää­see lop­pu­ti­laan myös kul­ke­mal­la en­sin ¬-kaa­ren ja sit­ten p-kaa­ren, jo­ten au­to­maat­ti hy­väk­syy 2:n pi­tui­sen merk­ki­jo­non ¬p. Lop­pu­ti­las­ta pää­see ta­kai­sin al­ku­ti­laan ∧-kaa­rel­la ja uu­del­leen lop­pu­ti­laan p-kaa­rel­la. Sik­si kaik­ki pa­rit­to­mat pi­tuu­det saa­daan merk­ki­jo­noil­la p, p∧p, p∧p∧p, … ja kaik­ki nol­laa suu­rem­mat pa­ril­li­set pi­tuu­det merk­ki­jo­noil­la ¬p, ¬p∧p, ¬p∧p∧p, …..

Vas­tauk­sis­sa esiin­tyi epä­tie­toi­suut­ta sii­tä, al­ka­vat­ko luon­nol­li­set lu­vut nol­las­ta vai yk­kö­ses­tä. Joil­la­kin ma­te­ma­tii­kan alueil­la on ta­pa­na aloit­taa nol­las­ta ja toi­sil­la yk­kö­ses­tä. Tie­to­jen­kä­sit­te­lys­sä aloi­te­taan mel­kein ai­na nol­las­ta. Kos­ka mo­lem­pia käy­tän­tö­jä esiin­tyy, kir­jois­sa, jul­kai­suis­sa ja kurs­seil­la ta­val­li­ses­ti mai­ni­taan, kum­paa käy­tän­töä nou­da­te­taan. Täl­lä­kin kurs­sil­la se on mai­nit­tu, mut­ta vas­ta nyt ym­mär­rän, et­tä se oli­si kan­nat­ta­nut mai­ni­ta myös ten­tin ky­sy­mys­pa­pe­ris­sa.

(f) Ol­koon n ku­van au­to­maa­tin hy­väk­sy­mäs­sä merk­ki­jo­nos­sa esiin­ty­vien merk­kien p mää­rä, ol­koon v sa­mas­sa merk­ki­jo­nos­sa esiin­ty­vien merk­kien ∨ mää­rä, ja ol­koon j sa­mas­sa merk­ki­jo­nos­sa esiin­ty­vien merk­kien ∧ mää­rä. Kir­joi­ta yk­sin­ker­tai­nen näi­tä lu­ku­ja kos­ke­va yh­tä­suu­ruus (jo­ta­kin tyy­liin 3j + 4 = n + 2v).

ok_text Oi­kein! modulo 19 f_nodes 7 hide_expr n = v+j+1 <=> tai

pe­rus­te­lu 1Ku­vas­ta on help­po tar­kas­taa, et­tä kul­je­taan mi­kä ∧- tai ∨-kaa­ri ta­han­sa, vä­lit­tö­mäs­ti si­tä en­nen on täy­ty­nyt kul­kea p-kaa­ri tai p-kaa­ri ja )-kaa­ri. Nii­den li­säk­si lop­pu­ti­laan tul­taes­sa on juu­ri kul­jet­tu jo­ko p-kaa­ri tai p-kaa­ri ja )-kaa­ri. pe­rus­te­lu 2Toi­saal­ta jo­kai­sen p-kaa­ren jäl­keen, jo­ko vä­lit­tö­mäs­ti tai he­ti )-kaa­ren jäl­keen, jo­ko kul­je­taan ∧- tai ∨-kaa­ri tai tul­laan lop­pu­ti­laan. pe­rus­te­lu 3Niin­pä kul­je­tut p-kaa­ret vas­taa­vat yk­si yh­teen kul­jet­tu­ja ∧-kaa­ria, kul­jet­tu­ja ∨-kaa­ria ja lo­pul­lis­ta lop­pu­ti­laan saa­pu­mis­ta. Sik­si kul­jet­tu­jen p-kaar­ten mää­rä eli n on yh­tä­suu­ri kuin kul­jet­tu­jen ∧-kaar­ten mää­rä plus kul­jet­tu­jen ∨-kaar­ten mää­rä plus lo­pul­lis­ten lop­pu­ti­laan saa­pu­mis­ten mää­rä. Toi­sin sa­noen n = j + v + 1.

2. (a) Kir­joi­ta sään­nöl­li­nen lau­se­ke, jo­ka tuot­taa täs­mäl­leen ne ku­van au­to­maa­tin hy­väk­sy­mät merk­ki­jo­not, jot­ka al­ka­vat mer­kil­lä ( ja jois­sa ) esiin­tyy vain vii­mei­se­nä.

Täl­le on mon­ta oi­keaa vas­taus­ta, jois­ta yk­si on tä­mä ”(”(¬p|p)∨(¬p|p)(∨(¬p|p))*”)” .

Vas­tauk­sen voi kek­siä näinSul­ku­ja kos­ke­vat eh­dot ra­joit­ta­vat merk­ki­jo­not nii­hin, jot­ka voi hy­väk­syä kul­ke­mal­la ala­kaut­ta al­ku­ti­las­ta lop­pu­ti­laan. Rei­til­lä on en­sin (, sit­ten jo­ko ¬p tai p, sit­ten ∨, sit­ten uu­del­leen jo­ko ¬p tai p, sit­ten nol­la tai useam­pia kier­rok­sia sil­mu­kas­sa, ja lo­puk­si ). Sil­mu­kas­sa on en­sin ∨ ja sit­ten jo­ko ¬p tai p. Koh­de­kie­len su­lut on syy­tä erot­taa jo­ten­kin me­ta­kie­len su­luis­ta, esi­mer­kik­si pa­ne­mal­la koh­de­kie­len su­lut ”lai­naus­merk­kei­hin”..

(b) Mi­ten voi­daan tes­ta­ta, tuot­taa­ko sään­nöl­li­nen lau­se­ke kaik­ki merk­ki­jo­not, jot­ka ky­sees­sä ole­vas­ta aak­kos­tos­ta voi tuot­taa?

vas­tausMuun­ne­taan sään­nöl­li­nen lau­se­ke NFA:ksi ja saa­tu NFA DFA:ksi. Täs­tä voi­daan jat­kaa eri ta­voil­la. Voi­daan esi­mer­kik­si mi­ni­moi­da DFA ja kat­soa, tu­li­ko yk­si­ti­lai­nen DFA, jon­ka al­ku­ti­la on lop­pu­ti­la, jos­ta on kaa­ri it­seen­sä jo­kai­sel­la aak­ko­sel­la.

Vas­tauk­sen voi kek­siä näinKurs­sil­la on esi­tet­ty al­go­rit­me­ja, jois­ta kan­nat­taa muis­taa ai­na­kin mi­tä ne saa­vat ai­kaan. Niis­tä voi ra­ken­taa mo­nen­lais­ta mel­kein kuin le­go­pa­li­kois­ta..

(c) Piir­rä NFA jon­ka hy­väk­sy­mä kie­li on sa­ma kuin vä­li­sym­bo­lin D tuot­ta­ma kie­li.

D:n kie­li­op­pi ja eräs oi­kea vas­taus

Vas­tauk­sen voi kek­siä näinL:n tuot­ta­mat merk­ki­jo­not saa­daan NFA:lla, jo­ka on muu­ten ku­ten vas­tauk­ses­sa, mut­ta ∨-kaa­ri ja ∧-kaa­ri puut­tu­vat. B ot­taa yh­den tai useam­man L:n tuot­ta­man merk­ki­jo­non, ja li­sää nii­den vä­liin ∧:n. Sa­ma vai­ku­tus saa­daan li­sää­mäl­lä ku­van ∧-kaa­ri. D ot­taa yh­den tai useam­man B:n tuot­ta­man merk­ki­jo­non, ja li­sää nii­den vä­liin ∨:n. Sa­ma vai­ku­tus saa­daan li­sää­mäl­lä ku­van ∨-kaa­ri..

3. (a) Kir­joi­ta jo­kin merk­ki­jo­no, jon­ka D tuot­taa mut­ta C ei tuo­ta. Piir­rä sen jä­sen­nys­puu.

Täs­sä voit ko­keil­la merk­ki­jo­nois­ta, täyt­ty­vät­kö eh­dot, ja voit piir­rät­tää jä­sen­nys­puun. Kos­ka mer­kit ∧, ∨ ja ¬ tuot­ta­vat han­ka­luuk­sia, niin ti­lal­la voi käyt­tää &, v ja -. Älä kir­joi­ta merk­ki­jo­noon vä­li­lyön­te­jä.
D tuot­taa
C ei tuo­ta
jä­sen­nys­puu
tai

Oi­kei­ta vas­tauk­sia on vaik­ka kuin­ka mon­ta. Yk­sin­ker­tai­sin niis­tä on tä­mäp∨p. On help­po näh­dä, et­tä C ei tuo­ta si­tä, kos­ka …C tuot­taa ∨:n vain G:n kaut­ta, mut­ta sil­loin mu­kaan tu­lee su­lut..

(b) On­ko C:n tuot­ta­ma kie­li sään­nöl­li­nen? Pe­rus­te­le. On­ko se yh­teys­riip­pu­ma­ton? Pe­rus­te­le.

On­ko se sään­nöl­li­nen? vas­taus Se on sään­nöl­li­nen, kos­ka ky­sy­mys­pa­pe­rin ku­vas­sa ole­va NFA hy­väk­syy sen.

On­ko se yh­teys­riip­pu­ma­ton? vas­taus Se on yh­teys­riip­pu­ma­ton, kos­ka jo­kai­nen sään­nöl­li­nen kie­li on yh­teys­riip­pu­ma­ton. (Yh­teys­riip­pu­mat­to­muu­den voi pe­rus­tel­la myös sil­lä, et­tä C:n kie­lel­le on esi­tet­ty ky­sy­mys­pa­pe­ris­sa BNF-mää­ri­tel­mä eli yh­teys­riip­pu­ma­ton kie­li­op­pi.)

(c) Kir­joi­ta kie­li­op­pi, jo­ka tuot­taa kie­len {abb, aabbbb, aaabbbbbb, …}. (Merk­ki­jo­nois­sa on en­sin jo­kin nol­laa suu­rem­pi mää­rä a:ta ja sit­ten kak­sin­ker­tai­nen mää­rä b:tä.)

Täs­sä voit ko­keil­la kie­li­op­pe­ja. Käy­tä kie­len ni­me­nä X.
ok_text Oi­kein! CFG_set X ::= abb | aXbb ; CFG_set2 ;CFG_compare
tai

Yk­si oi­kea vas­taus on tä­mäX ::= abb | aXbb.

4. Ali­oh­jel­ma f(σ) ot­taa syöt­teek­seen merk­ki­jo­non σ ja py­säh­tyy pa­laut­taen 0, 1, 2 tai 3. Jos f(σ) pa­laut­taa 0, niin σ:n si­säl­tö ei ole ali­oh­jel­ma. Jos f(σ) pa­laut­taa 1, niin σ:n si­säl­tö on ali­oh­jel­ma jo­ka py­säh­tyy tyh­jäl­lä syöt­teel­lä. Jos f(σ) pa­laut­taa 2, niin σ:n si­säl­tö on ali­oh­jel­ma jo­ka ei py­säh­dy tyh­jäl­lä syöt­teel­lä.

Jos yl­lä ole­va ku­vaus tun­tuu kum­mal­li­sel­ta, niin kan­nat­taa lu­kea tä­mäVas­tauk­sil­le 0, 1 ja 2 an­ne­tut ku­vauk­set ei­vät ole muo­toa ”jos ja vain jos”, vaan muo­toa ”jos … niin”. Siis ei esi­mer­kik­si lu­va­ta, et­tä jos σ:n si­säl­tö ei ole ali­oh­jel­ma, niin f(σ) pa­laut­taa 0. Jos σ:n si­säl­tö ei ole ali­oh­jel­ma, niin f(σ) ei voi pa­laut­taa 1 ei­kä 2, kos­ka 1:n ja 2:n ta­pauk­ses­sa σ:n si­säl­lön on ol­ta­va ali­oh­jel­ma; mut­ta voi pa­laut­taa 3, kos­ka 3:n ta­pauk­ses­sa σ:n si­säl­löl­le ei ole ase­tet­tu mi­tään ra­joi­tuk­sia. ja käy­dä lä­pi seu­raa­vat ky­sy­myk­set ja vas­tauk­set:

  ky­sy­mysJos σ:n si­säl­tö ei ole ali­oh­jel­ma, niin f(σ) pa­laut­taa vas­taus0 tai 3.

  ky­sy­mysJos σ:n si­säl­tö on ali­oh­jel­ma jo­ka py­säh­tyy tyh­jäl­lä syöt­teel­lä, niin f(σ) pa­laut­taa vas­taus1 tai 3.

  ky­sy­mysJos σ:n si­säl­tö on ali­oh­jel­ma jo­ka ei py­säh­dy tyh­jäl­lä syöt­teel­lä, niin f(σ) pa­laut­taa vas­taus2 tai 3.

  ky­sy­mysMi­kä on yk­sin­ker­tai­sin f(σ), jo­ka täyt­tää an­ne­tut eh­dot? vas­taus Sel­lai­nen, jo­ka pa­laut­taa ai­na 3, siis return 3.

(a) Pe­rus­te­le, et­tä on ole­mas­sa ai­na­kin yk­si σ, jol­le f(σ) pa­laut­taa 3. Et saa olet­taa tun­ne­tuk­si, et­tä tyh­jän syöt­teen py­säh­ty­mis­tes­te­riä ei ole.

Ku­va­tun kal­tai­nen ali­oh­jel­ma, jo­ka ei pa­lau­ta 3 mil­le­kään syöt­teel­le, te­kee hie­man enem­män kuin tyh­jän syöt­teen py­säh­ty­mis­tes­te­ri. Sen vas­tauk­set 0 ja 2 tar­koit­ta­vat sa­maa kuin tyh­jän syöt­teen py­säh­ty­mis­tes­te­rin vas­taus F, ja vas­taus 1 tar­koit­taa sa­maa kuin tyh­jän syöt­teen py­säh­ty­mis­tes­te­rin vas­taus T.

Teh­tä­vän ky­sy­mys tar­koit­taa siis, et­tä pi­tää to­dis­taa, et­tä tyh­jän syöt­teen py­säh­ty­mis­tes­te­riä ei ole ole­mas­sa. Täy­siin pis­tei­siin riit­tää mi­kä ta­han­sa vas­taus, jos­ta käy il­mi, et­tä vas­taa­ja ym­mär­tää jon­kin to­dis­tuk­sen pe­rus­idean. Yk­si to­dis­tus löy­tyy tääl­tä ja toi­nen tääl­tä.

(Täy­siin pis­tei­siin riit­täi­si myös pä­te­vä pe­rus­idea to­dis­tuk­sel­le, et­tä on ole­mas­sa syö­te, jol­le vas­tauk­sen pi­tää ol­la 0 tai 2, mut­ta f ei pys­ty sa­no­maan kum­pi. Sel­lais­ta pe­rus­ideaa ei kui­ten­kaan ole ole­mas­sa, kos­ka on ole­mas­sa ali­oh­jel­ma, jo­ka rat­kai­see ky­sy­myk­sen, esit­tää­kö an­net­tu merk­ki­jo­no ali­oh­jel­maa. Kään­tä­jiä­hän osa­taan teh­dä.)

(b) Pe­rus­te­le, et­tä on ole­mas­sa ää­ret­tö­män mon­ta σ, joil­le f(σ) pa­laut­taa 3. Saat käyt­tää (a)-koh­dan tu­los­ta apu­na.

vas­tausJos nii­tä oli­si vain ää­rel­li­nen mää­rä, niin f:n al­kuun voi­tai­siin li­sä­tä seu­raa­van­lai­nen if-then-else-ra­ken­ne. Sii­nä on haa­ra jo­kai­sel­le syöt­teel­le, jol­le al­ku­pe­räi­nen f pa­laut­taa 3. Haa­ra pa­laut­taa 0, 1 tai 2 sen mu­kaan, mi­kä on oi­kea vas­taus syöt­teel­le, jol­la jou­du­taan ky­sei­seen haa­raan. Näin f voi­tai­siin täy­den­tää sel­lai­sek­si, jo­ka ei kos­kaan pa­lau­ta 3. (a)-koh­dan mu­kaan sel­lais­ta täy­den­net­tyä f ei voi ol­la ole­mas­sa, jo­ten on ol­ta­va ää­ret­tö­män mon­ta σ, joil­le f(σ) pa­laut­taa 3.

Tä­mä idea kä­si­tel­tiin tääl­lä. Siel­lä osit­tai­nen tyh­jän syöt­teen py­säh­ty­mis­tes­te­ri vas­ta­si ”en tie­dä” jää­mäl­lä ikui­seen sil­muk­kaan, mut­ta nyt se vas­taa ”en tie­dä” pa­laut­ta­mal­la 3. Tä­mä ero ei ole olen­nai­nen.

(c) Jo­ko pe­rus­te­le, et­tä on ole­mas­sa merk­ki­jo­no, jol­le jo­kai­nen ku­va­tun­lai­nen ali­oh­jel­ma pa­laut­taa 3, tai pe­rus­te­le, et­tä sel­lais­ta merk­ki­jo­noa ei ole ole­mas­sa.

vas­tausSel­lais­ta merk­ki­jo­noa ei ole ole­mas­sa. Mil­le ta­han­sa merk­ki­jo­nol­le ρ jo­kin seu­raa­vis­ta kol­mes­ta on pä­te­vä f(σ), jo­ka ei pa­lau­ta ρ:lle 3:

if σ = ρ then return 0 else return 3

if σ = ρ then return 1 else return 3

if σ = ρ then return 2 else return 3

5. (a) (2 pis­tet­tä) Mi­tä tar­koit­taa merk­ki­jo­non Kol­mo­go­rov-komp­lek­si­suus? Täy­sien pis­tei­den vas­taus mah­tuu 10 sa­naan, jo­ten älä kir­joi­ta ko­vin pit­kää vas­taus­ta.

vas­tausLy­him­män syöt­teet­tö­män oh­jel­man pi­tuus, jo­ka tu­los­taa ky­sei­sen merk­ki­jo­non ja py­säh­tyy.

On pal­jon ti­lan­tei­ta, jois­sa jon­kin tie­don esit­tä­mi­seen käy­te­tyn muis­tin mää­rää voi­daan pie­nen­tää jol­lain hä­viöt­tö­mäl­lä pak­kaus­me­ne­tel­mäl­lä. Toi­set pak­kaus­me­ne­tel­mät tii­vis­tä­vät sa­man tie­don pie­nem­pään muis­tin mää­rään kuin toi­set. Täs­tä voi he­rä­tä aja­tus mi­ta­ta tie­don in­for­maa­tio­si­säl­töä sil­lä, kuin­ka pie­nek­si sen saa pa­kat­tua, jos pak­kaus­me­ne­tel­män saa va­li­ta va­paas­ti. Tä­mä aja­tus ei kui­ten­kaan toi­mi sel­lai­se­naan, kos­ka jos eri tie­dot pu­re­taan eri me­ne­tel­mil­lä, niin tie­don pur­ka­mi­sek­si tar­vi­taan pa­ka­tun tie­don li­säk­si tie­to sii­tä, mil­lä me­ne­tel­mäl­lä se pi­tää pur­kaa.

Toi­mi­vam­pi in­for­maa­tion mää­rän mit­ta on mah­dol­li­sim­man pie­nen sel­lai­sen pa­ke­tin ko­ko, jos­ta yk­si ja sa­ma, kai­kil­le pa­ka­tuil­le tie­doil­le yh­tei­nen oh­jel­ma pur­kaa tie­don yh­tä ja sa­maa nap­pia pai­na­mal­la, il­man mi­tään li­sä­in­for­maa­tio­ta. Jot­ta tie­don pak­kaa­mi­ses­sa voi­tai­siin käyt­tää mi­tä ta­han­sa nyt tun­net­tua tai tu­le­vai­suu­des­sa kek­sit­tä­vää pak­kaus­me­ne­tel­mää, pur­ku­oh­jei­den pi­tää ol­la esi­tet­ty­nä pa­ke­tis­sa mah­dol­li­sim­man yleis­pä­te­väl­lä ta­val­la. Kä­sit­teel­lä ”mah­dol­li­sim­man yleis­pä­te­vä oh­jei­den esit­tä­mis­ta­pa” on ni­mi: oh­jel­moin­ti­kie­li.

Pa­ke­tis­sa on siis esi­tet­tä­vä se­kä pa­kat­tu tie­to et­tä sen pur­ka­mi­seen käy­tet­tä­vä oh­jel­ma. Kos­ka pa­kat­tu tie­to voi­daan kir­joit­taa li­te­raa­li­va­kioi­na oh­jel­man si­sään, ja­koa pa­kat­tuun tie­toon ja pur­ka­mis­oh­jel­maan ei tar­vi­ta, vaan riit­tää pu­hua oh­jel­mas­ta. Pa­ke­tis­sa on siis oh­jel­ma, jo­ka ei lue syö­tet­tä. Yh­tei­nen pur­ku­oh­jel­ma ei tee muu­ta kuin ajaa tä­män oh­jel­man.

Näin on pääs­ty vas­tauk­ses­sa esi­tet­tyyn Kol­mo­go­rov-komp­lek­si­suu­den kä­sit­tee­seen. Asiaa on kä­si­tel­ty pe­rus­teel­li­ses­ti teh­tä­väs­sä Da­tan pak­kaa­mi­nen ja Kol­mo­go­rov-komp­lek­si­suus.

(b) (4 pis­tet­tä) Kir­joi­ta en­nal­ta miet­ti­mä­si es­see.

Al­la ole­va es­see on eh­kä hie­man liian pit­kä, mut­ta muis­sa suh­teis­sa se on esi­merk­ki nel­jän pis­teen es­sees­tä. Sii­nä on esi­tet­ty jo­kin kurs­sin ai­he­pii­riin liit­ty­vä epä­tri­viaa­li asia täs­mäl­li­ses­ti ma­te­maat­ti­sia mer­kin­tö­jä hyö­dyn­täen. Sen asia­si­säl­tö ei ole suo­ra ko­pio läh­teis­tä, vaan sii­nä on mu­ka­na omaa luo­vuut­ta. Sii­nä ei (toi­vot­ta­vas­ti ☺) ole asia­vir­hei­tä.

Lii­ka pi­tuus joh­tuu sii­tä, et­tä ha­lu­sin näyt­tää ten­tin ky­sy­mys­pa­pe­ris­sa esiin­ty­vät kie­li­opit. Es­sees­tä sai­si ly­hyem­män pis­teet säi­lyt­täen jät­tä­mäl­lä pois dis­junk­tii­vi­sen nor­maa­li­muo­don tai ete­ne­mäl­lä no­peam­min kon­junk­tii­vi­sen nor­maa­li­muo­don vii­mei­seen kie­li­op­piin.

Pro­po­si­tio­lo­gii­kan nor­maa­li­muo­dot il­man tur­hia sul­ku­ja

Pro­po­si­tio­lo­gii­kan kaa­va on dis­junk­tii­vi­ses­sa nor­maa­li­muo­dos­sa, jos ja vain jos sen ra­ken­ne on seu­raa­va. Se koos­tuu yh­des­tä tai useam­mas­ta osas­ta, jot­ka on yh­dis­tet­ty toi­siin­sa tai-ope­raat­to­ril­la eli ∨:lla. Jo­kai­nen osa koos­tuu yh­des­tä tai useam­mas­ta li­te­raa­lis­ta, jot­ka on yh­dis­tet­ty toi­siin­sa ja-ope­raat­to­ril­la eli ∧:lla. Li­te­raa­li on pro­po­si­tio­sym­bo­li tai pro­po­si­tio­sym­bo­lin ne­gaa­tio, eli muo­toa p tai ¬p. Seu­raa­va kie­li­op­pi esit­tää tä­män ra­ken­teen il­man sul­ku­ja.

D  ::=  B  |  D ∨ B
B  ::=  L  |  B ∧ L
L  ::=  p  |  ¬p

Pro­po­si­tio­lo­gii­kan kaa­va on kon­junk­tii­vi­ses­sa nor­maa­li­muo­dos­sa, jos ja vain jos sen ra­ken­ne on seu­raa­va. Se koos­tuu yh­des­tä tai useam­mas­ta klau­suu­lis­ta, jot­ka on yh­dis­tet­ty toi­siin­sa ∧:lla. Klau­suu­li koos­tuu yh­des­tä tai useam­mas­ta li­te­raa­lis­ta, jot­ka on yh­dis­tet­ty toi­siin­sa ∨:lla. Ku­ten edel­lä, li­te­raa­li on pro­po­si­tio­sym­bo­li tai pro­po­si­tio­sym­bo­lin ne­gaa­tio. Seu­raa­va kie­li­op­pi esit­tää tä­män ra­ken­teen si­ten, et­tä jo­kai­sen klau­suu­lin ym­pä­ril­lä on su­lut. Su­luil­la var­mis­te­taan, et­tä ope­raat­to­rien ∧ ja ∨ vä­li­nen las­ku­jär­jes­tys säi­lyy oi­kea­na.

C  ::=  (K)  |  C ∧ (K)
K  ::=  L  |  K ∨ L
L  ::=  p  |  ¬p

Tä­mä kie­li­op­pi vaa­tii enem­män sul­ku­ja kuin on vält­tä­mä­tön­tä. Su­lut tar­vi­taan sil­loin ja vain sil­loin, kun ∧:n alai­suu­des­sa on ∨. Su­lut voi­daan siis jät­tää pois klau­suu­leis­ta, jois­sa on vain yk­si li­te­raa­li. Seu­raa­vas­sa kie­li­opis­sa G esit­tää klau­suu­lit, jois­sa on ai­na­kin kak­si li­te­raa­lia. C ra­ken­ne­taan niis­tä su­lu­tet­tui­na ja/tai yk­sit­täi­sis­tä li­te­raa­leis­ta il­man sul­ku­ja.

C  ::=  L  |  (G)  |  C ∧ L  |  C ∧ (G)
G  ::=  L ∨ L  |  G ∨ L
L  ::=  p  |  ¬p

Sul­ku­ja ei tar­vi­ta myös­kään sil­loin, kun ∧-ope­raat­to­rei­ta ei ole lain­kaan. Seu­raa­va kie­li­op­pi esit­tää kon­junk­tii­vi­sen nor­maa­li­muo­don il­man tur­hia sul­ku­ja.

C  ::=  K  |  A ∧ L  |  A ∧ (K ∨ L)
K  ::=  L  |  K ∨ L
A  ::=  L  |  (K ∨ L)  |  A ∧ L  |  A ∧ (K ∨ L)
L  ::=  p  |  ¬p