Tehtävä:
Shannonin alaraja
Lyhyt MathCheck-ohje (uuteen välilehteen)
Shannonin informaatioteoria käsittelee sitä, kuinka tiiviisti informaatiota voi pakata. Tässä tehtävässä tutustutaan muutamaan perusasiaan häviöttömän pakkauksen tapauksessa, eli tilanteessa, jossa pakattu informaatio täytyy pystyä palauttamaan virheettömästi. Aihepiiri tarjoaa mahdollisuuden harjoitella mm. induktiotodistusta bittijonoista koostuville joukoille.
Häviöttömän pakkauksen vastakohta on häviöllinen pakkaus, mikä tarkoittaa, että informaatio saa pikkuisen muuttua jos pakattu tiedosto pienenee tuntuvasti. Häviöllisiä menetelmiä käytetään laajasti esimerkiksi valokuvia ja musiikkia pakattaessa.
Vaihtelevanpituiset koodit
Oletamme, että erilaisia merkkejä on ainakin kaksi. Jos ihmettelet, miksi tällainen rajoittava oletus tehdään, niin mieti hetki miten tekstejä voi kirjoittaa, jos käytettävissä on vain yksi tai nolla erilaista merkkiä.
Tarkastellaan pitkän suomenkielisen tekstin esittämistä bittijonona. Tekstissä voi esiintyä pieniä ja isoja kirjaimia, välilyöntejä sekä joitakin välimerkkejä ja kenties muitakin merkkejä, kuten numeroita. Jos erilaisia merkkejä on `n`, yksinkertaisinta on esittää kukin merkki `|~log_2 n~|` bitillä. Tämä ei kuitenkaan ole muistin käytön kannalta tehokasta, koska toiset merkit ovat paljon harvinaisempia kuin toiset. Esimerkiksi q on harvinainen ja e yleinen suomenkielisissä teksteissä.
Tehokkaampaan esitystapaan päästään käyttämällä yleisille merkeille vähemmän bittejä kuin harvinaisille. Tässä tehtävässä tutkitaan, kuinka tämä kannattaa tehdä ja miten vähällä määrällä bittejä voidaan selvitä.
Annamme ensin symbolit jatkossa tarvittaville käsitteille ja tutustumme niihin esimerkin avulla. Oikeassa käyttötilanteessa tekstien on tarkoitus olla pitkiä, mutta esimerkki on lyhyt, jotta se ei olisi kovin työläs. Merkitsemme erilaisten merkkien määrää `n`:llä ja annamme niille indeksit 1, …, `n`. Jos merkit ovat
1 2 3 4 n k a s
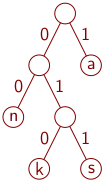Merkkien esitystavat bittikuvioina muodostavat koodin.
Käytämme ananaskana-esimerkissä seuraavaa koodia:
1 2 3 4 n k a s 00 010 1 011
Tekstiä lukevan ohjelman on tiedettävä käytetty koodi. Yksi mahdollisuus on kertoa se ennen tekstiä. Se lisää kaikkiaan tarvittavien bittien määrää niin paljon, että hyöty menetetään, jos teksti on lyhyt. Pitkien tekstien tapauksessa menetelmä on silti kannattava. Voidaan myös tehdä niin, että merkkien esiintymistiheyksiä ei lasketa siitä tekstistä joka halutaan esittää, vaan lukuina `p_i` käytetään täällä julkaistuja merkkien esiintymistiheyksiä suomenkielessä.
Siis, kun luvut `p_i` on annettu, tavoitteena on valita koodi siten, että `sum_(i=1)^n p_i l_i` on mahdollisimman pieni. Sellainen koodi on optimaalinen.
Mitä pienempiä bittikuvioiden pituudet eli luvut `l_i` ovat, sitä pienempi tästä summasta tulee. Koodia ei voi kuitenkaan valita miten tahansa. Ei esimerkiksi voida valita bittikuvioiksi 0, 01 ja 10, koska silloin ei tiedettäisi, tulisiko 010 tulkita 0-10 vai 01-0. Tämä on sama kysymys kuin koostuuko yhdyssana ”kaivosaukko” osista ”kaivo” ja ”saukko” vai ”kaivos” ja ”aukko”.
Tästä ei kuitenkaan seuraa, että isolla `n` ei voitaisi lainkaan käyttää lyhyitä bittikuvioita. Aina voidaan saada yksi `l_i` ykköseksi valitsemalla yhden merkin bittikuvioksi 0 ja kaikille muille merkeille 1-alkuinen bittikuvio.
Niinpä lukujen `l_i` arvoja säätelee monimutkainen ehto. Seuraavaksi selvitämme tarkasti, mikä tämä ehto on.
Kraftin epäyhtälö
Kun eri merkit käyttävät eri määrän bittejä, ongelmaksi tulee, miten tiedetään missä edellisen merkin bittikuvio loppuu ja seuraavan alkaa. Yksinkertaisin ja eniten käytetty ratkaisu on sopia, että minkään merkin bittikuvio ei saa olla toisen merkin bittikuvion aito alkuosa. (Bittijonon aito alkuosa on alkuosa, joka on lyhyempi kuin bittijono itse.) Jos siis jollekin merkille on annettu bittikuvioksi 0100, bittikuvioita 01000, 01001, 010000 jne. ei voi antaa millekään merkille. Kutsumme tätä alkuosaehdoksi.
Kun koodi esitetään puuna, alkuosaehto tarkoittaa, että merkkejä esiintyy vain
lehdissä eli solmuissa, joista puu ei jatku alaspäin.
Jokainen alkuosaehtoa noudattava koodi toteuttaa Kraftin epäyhtälön, joka on seuraava. Olkoot käytössä olevien bittikuvioiden pituudet `l_1`, …, `l_n`. Silloin
`sum_(i=1)^n 2^(-l_i)``<=``1` .
Kokeillaan! Laske ym. summa, kun bittikuviot ovat annetut. Alimmassa tapauksessa ei noudateta alkuosaehtoa.
Jos B sisältää tyhjän bittijonon, niin muuta siinä ei voi ollakaan, koska …Tyhjä bittijono on jokaisen muun bittijonon aito alkuosa, ja alkuosaehto kieltää joukon alkiota olemasta toisen alkion aito alkuosa. Olemme jo todistaneet Kraftin epäyhtälön tässä tilanteessa. Se oli induktion pohjatapaus.
Muussa tapauksessa B koostuu bittijonoista muotoa 0β tai 1β, missä β on …bittijono, jonka pituus on enintään `n`. Olkoon B0 = { β | 0β ∈ B } eli …niiden β joukko, joille 0β ∈ B eli joukko, joka saadaan poistamalla nollalla alkavista B:n alkioista alun nollat., ja olkoon B1 = { β | 1β ∈ B }. Näiden joukkojen alkiot ovat pituudeltaan enintään …`n`. Jos α ∈ B0 ja β ∈ B0 niin 0α ∈ B ja 0β ∈ B, joten α ei voi olla β:n aito alkuosa, koska …muutoin 0α olisi 0β:n aito alkuosa, vastoin oletusta että B noudattaa alkuosaehtoa. Näin ollen B0 noudattaa alkuosaehtoa. …Induktio-oletuksen vuoksi se noudattaa myös Kraftin epäyhtälöä. Emme merkitse summaan mitä arvoja `i` saa vaan joukon nimen B0, koska joukon nimi on tässä tilanteessa selkeämpi kuin indeksit. Siis `sum_(B_0) 2^(-l_i)``<=``1`. Sama päättely pätee myös B1:lle, joten `sum_(B_1) 2^(-l_i)``<=``1`.
Koska B:n alkiot saadaan lisäämällä B0:n alkioiden eteen 0 (jolloin pituus kasvaa yhdellä) ja B1:n alkioiden eteen 1, pätee
`sum_B 2^(-l_i) =`…`sum_(B_0) 2^(-(l_i+1)) + sum_(B_1) 2^(-(l_i+1))`
Induktioaskel ja samalla Kraftin epäyhtälön todistus on valmis.
Kraftin epäyhtälöä kutsutaan Kraftin epäyhtälöksi, koska Leon Kraft esitti sen gradussaan vuonna 1949 ja kertoi, että Raymond Redheffer oli keksinyt sen. Brockway McMillan todisti vuonna 1956, että se pätee yleisemmin kuin mitä edellä todistettiin. Se pätee kaikille koodeille, joissa kaksi eri merkkijonoa ei koskaan tuota samaa bittijonoa. Siksi tätä epäyhtälöä kutsutaan myös Kraft–McMillanin epäyhtälöksi.
Huffmanin koodi
Luku `sum_(i=1)^n p_i l_i` saadaan mahdollisimman pieneksi Huffmanin koodilla. Se muodostetaan seuraavasti. Jos eri merkkejä on vain kaksi, toiselle niistä annetaan bittikuvioksi 0 ja toiselle 1. Muussa tapauksessa valitaan kaksi eri merkkiä, joille `p_i` on mahdollisimman pieni. Olkoot niiden indeksit `j` ja `k`. Sitten rakennetaan Huffmanin koodi muunnetulle merkistölle, jossa valittujen kahden merkin sijalla on yksi merkki, jonka esiintymistiheys on `p_j + p_k`. Olkoon β se bittikuvio, jonka yhdistetty merkki saa tässä koodissa. Merkeille `j` ja `k` annetaan bittikuvioiksi β0 ja β1, ja β poistetaan.
Ananaskana-esimerkissä harvinaisimmat merkit ovat k ja s, joten ne yhdistetään merkiksi ks ja etsitään Huffmanin koodi merkistölle {n, a, ks}. Sen harvinaisimmat merkit ovat ks ja n, joten ne yhdistetään ja etsitään Huffmanin koodi merkistölle {ksn, a}. Nyt valitaan ksn:n bittikuvioksi 0 ja a:n bittikuvioksi 1. (Aivan yhtä hyvin olisi voitu valita toisinpäin.) Koska ksn tehtiin yhdistämällä ks ja n, lisätään sen bittikuvion eli 0:n perään 0, jolloin saadaan n:n bittikuvio 00, ja 1, jolloin saadaan ks:n bittikuvio 01. Viimeisessä vaiheessa ks:n bittikuviosta tehdään k:n bittikuvio 010 ja s:n bittikuvio 011. Näin saatiin edellä käytetyt bittikuviot.
Se, että Huffmanin koodi toteuttaa alkuosaehdon, seuraa induktiolla siitä miten se muodostetaan.
- Induktion pohjatapaus on se, jossa …Merkkejä on vain kaksi. Se pätee, koska …Silloin bittikuviot ovat 0 ja 1, ja niistä kumpikaan ei ole toisen aito alkuosa.
- Induktioaskel on se, jossa muodostetaan bittikuviot β0 ja β1. Täytyy todistaa, että kumpikaan niistä ei ole minkään uudessa koodissa käytetyn bittikuvion aito alkuosa eikä toisinpäin. Niistä kumpikaan ei ole toisensa aito alkuosa. Myöskään β0 ja β1 eivät voi olla minkään vanhaan koodiin kuuluvan α:n aitoja alkuosia, koska …muutoin β olisi α:n aito alkuosa, vastoin induktio-oletusta. Induktio-oletuksen mukaan …mikään vanhaan koodiin kuuluva α ei ole β:n aito alkuosa, joten se ei voi olla myöskään β0:n eikä β1:n aito alkuosa yhtä poikkeusta lukuunottamatta. Se poikkeus on …α = β, ja se ei riko väitettä, koska …β ei ole mukana uudessa koodissa.
Todistaaksemme, että Huffmanin koodi minimoi luvun `sum_(i=1)^n p_i l_i`, huomaamme alkajaisiksi, että optimaalisella koodilla on seuraavat ominaisuudet:
- Jos siinä on bittikuvio joka alkaa β0, niin siinä on myös bittikuvio joka alkaa β1. Tämä pätee, koska …Muutoin koodia voitaisiin parantaa korvaamalla jokainen β0α βα:lla. Tämä on ilmeistä kun ajattelet koodin esitystä puuna. Sama pätee tietysti myös toisinpäin. Tästä seuraa, että ainakin kaksi siihen kuuluvaa bittikuviota on maksimaalisia, eli mikään muu siihen kuuluva bittikuvio ei ole niitä pitempi. Muutoinhan …ainoa maksimaalinen bittikuvio olisi β0 ilman β1:stä tai toisinpäin.
Karkeasti sanottuna, kaksi harvinaisinta merkkiä käyttää kaksi pisintä bittikuviota. Tarkemmin sanottuna, on olemassa kaksi merkkiä siten, että mikään merkki ei ole niistä kumpaakaan harvinaisempi, ja kummallakin niistä on bittikuvio, jota pitempiä ei koodissa ole. Tämä pätee, koska …Edellä todistettiin, että ainakin kahdella merkillä on maksimaalinen bittikuvio. Valitaan tarkasteluun kaksi mahdollisimman harvinaista merkkiä. Jos vaihtoehtoja on useita, valitaan sellaiset, joilla on mahdollisimman pitkät bittikuviot. Jos jomman kumman niistä bittikuvio ei ole maksimaalinen, niin jollakin sitä vähemmän harvinaisella merkillä on maksimaalinen bittikuvio. Koodi paranisi vaihtamalla näiden kahden merkin bittikuviot keskenään, jolloin alkuperäinen koodi ei olisikaan optimaalinen vastoin lähtöoletustamme.
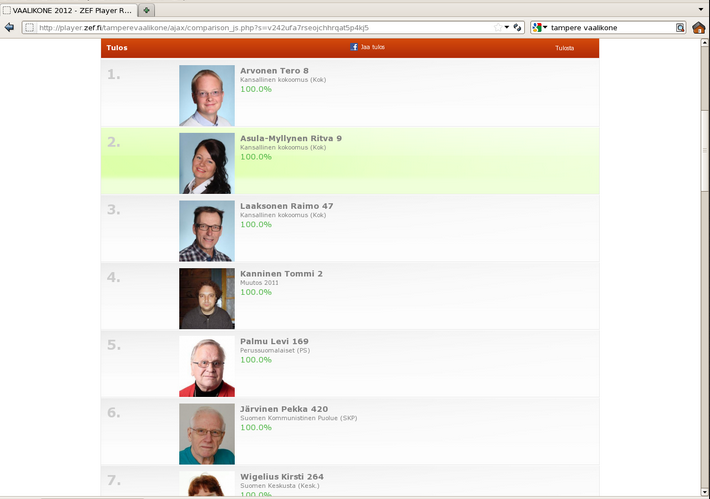
Voit lukea tästäOhjelmoijien on yllättävän vaikea ottaa huomioon, että aina ei ole sallittua käsitellä yhtä hyviä tapauksia ikään kuin jokin olisi muita parempi. Esimerkiksi vaalikone ei ole reilu, ellei se näytä yhtä hyvät osumat saaneita ehdokkaita tasaveroisina. Oheinen kuva näyttää, että Tampereella vuoden 2012 kunnallisvaaleissa käytetty vaalikone ei ollut reilu. Kuva saatiin vastaamalla liikennepoliittisiin kysymyksiin ja jättämällä muut kohdat tyhjiksi. Kaikkiaan 20 ehdokasta oli antanut täsmälleen samat vastaukset.
tositapahtuman, joka havainnollistaa, miksi edellä käytetty karkea puhetapa ei
riitä, vaan tarvitsee sanoa tarkemmin.
- Sanomme, että kaksi merkkiä ovat bittikuviopari, jos ja vain jos niiden bittikuviot ovat viimeistä bittiä vaille samat eli muotoa β0 ja β1. Koodin optimaalisuus ei takaa, että edellä mainitut kaksi mahdollisimman harvinaista merkkiä ovat bittikuviopari. Se ei myöskään estä sitä, sillä ne saadaan bittikuviopariksi optimaalisuutta menettämättä tällä tavallaOlkoot ne a ja b, ja olkoon c se merkki, jonka kanssa b muodostaa bittikuvioparin. Vaihdetaan a:n ja c:n bittikuviot keskenään. Kumpikin vaihdettava bittikuvio on maksimaalinen, joten mikään `l_i` ei muutu.. Kokonaistodistuksen kannalta tämä tarkoittaa, että emme todista, että Huffmanin algoritmi löytää kaikki optimaaliset koodit, vaan että se löytää jonkin optimaalisen koodin.
Näillä eväillä voimme todistaa Huffmanin koodin optimaalisuuden induktiolla.
- Induktion pohjatapauksessa on kaksi merkkiä ja niiden bittikuviot ovat 0 ja 1. Se on selvästi optimaalinen koodi.
Induktioaskeleessa osoitetaan, että Huffmanin algoritmin rekursioaskel tuottaa optimaalisen uuden koodin (sen, jossa on β0 ja β1) vanhasta koodista (siitä, jossa on β). Induktio-oletus sanoo, että …Vanha koodi on optimaalinen. Bittikuviopari tehdään kahdesta mahdollisimman harvinaisesta merkistä. Olemme osoittaneet, että se ei pilaa optimaalisuutta. Vanhan koodin β esittää merkkiä, jonka esiintymistiheys on `p_j + p_k` ja jolle `l_i =`|β|. Uuden koodin β0 ja β1 esittävät merkkejä, joiden esiintymistiheydet ovat …`p_j` ja `p_k` ja joille `l_i =` …|β| + 1 Niinpä vanhasta koodista uuteen siirryttäessä `sum_(i=1)^n p_i l_i` kasvaa luvun …`p_j(|beta| + 1) + p_k(|beta| + 1) - (p_j+p_k)|beta|``=``p_j + p_k` verran.
Siksi uusi koodi minimoi luvun `sum_(i=1)^n p_i l_i` jos ja vain jos vanha koodi minimoi luvun `sum_(i=1)^n p_i l_i - (p_j + p_k)`. Jälkimmäinen on sama asia kuin että vanha koodi minimoi luvun `sum_(i=1)^n p_i l_i`, koska `p_j + p_k` ei riipu siitä, minkälainen vanha koodi on. Induktio-oletus lupaa, että vanha koodi tekee tämän, joten uusi koodi on optimaalinen.
Huffman keksi koodinsa vuonna 1951 kirjoittaessaan projektiraporttia, jolla saattoi korvata tentin. Hänen ohjaajansa oli itsekin yrittänyt keksiä optimaalisen koodin, mutta ei ollut onnistunut.
Shannonin alaraja
Todistamme induktiolla, että tässä tapauksessa Huffmanin algoritmi takaa jokaiselle merkille, että `l_i``=``-log_2 p_i`.
- Pohjatapauksessa on vain kaksi merkkiä. Silloin `p_1``=``p_2``=``2^(-1)`, koska …Kahdella harvinaisimmalla merkillä on sama esiintymistiheys ja `sum_(i=1)^n p_i``=``1`. Merkkien bittikuviot ovat 0 ja 1, joten `l_1``=``l_2``=`1`= -log_2 2^(-1)`.
Tässä erikoistapauksessa saamme `sum_(i=1)^n p_i l_i``=``-sum_(i=1)^n p_i log_2 p_i`.
Yleisessä tapauksessa ei voi aina olla `l_i``=``-log_2 p_i`, koska `l_i` on luonnollinen luku mutta `-log_2 p_i` ei välttämättä ole luonnollinen luku. Yleisessä tapauksessa pätee
`sum_(i=1)^n p_i l_i``>=``-sum_(i=1)^n p_i log_2 p_i` .
Se voidaan todistaa — yllätys, yllätys! — induktiolla. Todistus on mukana täydellisyyden vuoksi ja esimerkkinä siitä, että tällaisiakin laskelmia tarvitaan. Kurssin kannalta se ei kuitenkaan ole keskeinen, joten saat hypätä sen yli lähellä loppua oleviin kysymyksiin, jos se ei kiinnosta. Olkoon
`f(x)``=``x log_2 x + (1-x) log_2 (1-x)` .
Induktion pohjatapauksessa on kaksi merkkiä, joten `n=2` ja
`p_2``=``1-p_1`.
Siksi, ja ruskeiden kohtien alla esitettyjen perustelujen vuoksi,
`sum_(i=1)^n p_i l_i``=`Koska
bittikuviot ovat 0 ja 1, pätee `l_1=l_2=1`.`p_1 + p_2``=``1`
`>=`Edellä todistetun
perusteella `f(p_1)``>=``-1`, joten
`-f(p_1)``<=``1`.`-(p_1 log_2 p_1 + (1-p_1) log_2 (1-p_1))`
`=``-sum_(i=1)^n p_i log_2 p_i` .
Induktioaskelta varten indeksoimme merkit uudelleen siten, että ensin ovat
ne, joiden bittikuvio alkaa 0:lla, ja sitten ne, joiden bittikuvio alkaa
1:llä.
Olkoon `n_0` 0-alkuisten bittikuvioiden määrä.
Merkitsemme `q``=``sum_(i=1)^(n_0) p_i`.
Tällöin
`sum_(i=1)^n p_i l_i`
`=`Yhtäsuuruus saadaan
sieventämällä `q`:t ja `(1-q)`:t pois, yhdistämällä summat, kertomalla
`(l_i-1)` auki ja huomaamalla, että `1 + sum_(i=1)^n p_i(-1)``=``1 -
sum_(i=1)^n p_i``=``0`.`1 + q sum_(i=1)^(n_0) p_i/q (l_i-1) +
(1-q) sum_(i=n_0+1)^n p_i/(1-q) (l_i-1)`
`>=`Ensimmäinen summa vastaa
koodia, joka koostuu 0:lla alkavien bittikuvioiden loppuosista ilman ko. 0:aa,
ja jälkimmäinen summa vastaa koodia, joka koostuu 1:llä alkavien
bittikuvioiden loppuosista ilman ko. 1:stä.
Jakajat `q` ja `1-q` huolehtivat, että kummankin näistä koodeista sisällä
esiintymistiheyksien summa on 1.
Epäyhtälö saadaan soveltamalla näihin koodeihin
induktio-oletusta.`1 - q sum_(i=1)^(n_0) p_i/q log_2 (p_i/q) -
(1-q) sum_(i=n_0+1)^n p_i/(1-q) log_2 (p_i/(1-q))`
`=`On käytetty mm. kaavaa `log_2
(p_i/x)``=``log_2 p_i - log_2 x` sekä sitä, että 0-alkuisten koodin kaikkien
merkkien esiintymistiheyksien summa on 1, ja samoin 1-alkuisten
koodille.`1 - sum_(i=1)^(n_0) p_i log_2 p_i + q log_2 q -
sum_(i=n_0+1)^n p_i log_2 p_i + (1-q) log_2 (1-q)`
`=`Summat on yhdistetty ja ykkönen
siirretty summan perään.`-sum_(i=1)^n p_i log_2 p_i + 1 + q
log_2 q + (1-q) log_2 (1-q)`
`>=`Edellä todistetun
perusteella `f(q)``>=``-1`.`-sum_(i=1)^n p_i log_2 p_i` .
Tämä on Claude Shannonin vuonna 1948 todistama alaraja sille, kuinka tiiviisti tietoa voidaan pakata, jos oletetaan, että merkkien esiintyminen on toisistaan riippumatonta. (Oletus ei aina päde: esimerkiksi suomenkielessä seuraava merkki on hyvin harvoin t, jos kaksi edellistä ovat olleet t. Shannonin teoria on kuitenkin erinomainen alku tiedon pakkaamisen tutkimiselle.)