Tehtävä:
Sarjalle Θ-merkintä helposti
Lyhyt MathCheck-ohje (uuteen välilehteen)
Algoritmien suorituskyvyn analyysissa tulee usein laskettavaksi muotoa `f(1)``+``f(2)``+``...``+``f(n)` olevan sarjan summa, missä `0``<=``f(1)` ja `f(x)``<=``f(y)` aina kun `1``<=``x``<=``y``<=``n`. Sarjan alkukohta voi olla myös esimerkiksi `0` ja loppukohta esimerkiksi `n-1`. Joskus summan tarkka arvo on helppo laskea, mutta usein se on toivottoman vaikeaa. Algoritmien analyysissa ei kuitenkaan juuri koskaan tarvita tarkkaa arvoa, vaan `Theta`-merkinnän tarkkuus riittää. Tässä tehtävässä opettelemme helpon kikan, joka toimii melkein (mutta ei aivan) aina ja joka tuottaa vastauksen sillä tarkkuudella.
Käyttölupaehto
Pohtikaamme aluksi hetki, miksi juuri tuon muotoiset sarjat ovat yleisiä. Usein algoritmissa on silmukka, joka käsittelee taulukon tms. osaa, joka kasvaa kierros kierrokselta. Esimerkiksi insertion-sortin pääsilmukassa sijoitetaan alkio paikalleen osataulukkoon, jonka koko on ensimmäisellä kierroksella 1, toisella kierroksella 2 ja niin edelleen, kunnes se on viimeisellä kierroksella yhtä pienempi kuin `n` eli koko taulukon koko. Osataulukkoa selataan lopusta alkaen ja sen alkioita siirretään yksi askel oikealle, kunnes uuden alkion paikka on löytynyt. Huonoimmassa tapauksessa joudutaan selaamaan koko osataulukko. Huonoimman tapauksen työmäärä on siis yksittäisellä kierroksella suoraan verrannollinen osataulukon kokoon ja yhteensä suoraan verrannollinen käsiteltävien osataulukoiden kokojen summaan eli lukuun `1``+``2``+``...``+``(n-1)`.
Entä jos taulukon tms. osa ei kasvakaan kierros kierrokselta, vaan vähenee kierros kierrokselta? VastausSilloin takaperin käännetty eli lopusta alkuun laskettu sarja täyttää ehdot. Sen summa on sama kuin alkuperäisen sarjan summa, joten tämän tehtävän kikkaa voi käyttää.
Koska ajan ja muistin kulutus eivät voi olla negatiivisia, voimme olettaa, että ensimmäinen termi on vähintään 0. Toisinaan tämä ehto rikkoutuu näennäisesti. On esimerkiksi varsin tavallista, että silmukan yhdellä kierroksella tehtävä työmäärä on `Theta(log n)`. Jos ensimmäisellä kierroksella käsitellään tyhjää tietorakennetta, sarja alkaa `log 0 + ...` eli ensimmäinen termi on `-oo`. Tällöin ensimmäinen termi ei kuitenkaan kuvasta todellista työmäärää. `Theta`-merkinnän määritelmä sallii ensimmäisen ja toisen termin (itse asiassa minkä tahansa kiinteän määrän termejä) olla mitä tahansa; vaaditaan ainoastaan, että on olemassa jokin raja, josta alkaen termit kuvaavat kasvuvauhtia oikein. Tästä syystä ensimmäinen termi saattaa olla ihan humpuukia.
Toisaalta samasta syystä `Theta`-merkinnän määritelmä sallii jättää sarjan alusta yhden tai kaksi termiä pois. Niinpä, jos `f(0)``>=``0` tai `f(1)``>=``0` ei päde, on luvallista aloittaa sarja termistä `f(1)` tai `f(2)`, tai vaikka termistä `f(37)`.
Saako negatiiviset termit jättää pois seuraavien sarjojen summan `Theta`-merkintää laskettaessa? Miksi saa tai miksi ei saa?
Koska silmukan käsittelemä tietorakenne tyypillisesti kasvaa kierros kierrokselta, ja koska isomman tietorakenteen käsittelyyn menee tyypillisesti enemmän aikaa kuin pienemmän, `f(1)``<=``f(2)``<=``...``<=``f(n)` pätee tyypillisesti. Tulemme tarvitsemaan hieman vahvempaa oletusta
`f(2/2)``<=``f(3/2)``<=``...``<=``f((2n)/2)`.
Tämä oletus on kuitenkin kömpelöä muotoa. Suoritusaikaa kuvaamaan käytetyt funktiot noudattavat yleensä yksinkertaisempaa, vielä vahvempaa oletusta: ne ovat kasvavia reaalilukuvälillä `1``<=``x``<=``n`. Alussa annettu oletus sanoo juuri tämän.
Tarkasteltava sarja ei kuitenkaan aina ole todellisesta algoritmista peräisin, ja algoritmeissakin saattaa esiintyä poikkeuksia. Siksi on syytä aina aloittaa varmistautumalla, että ehdot todellakin pätevät, kenties sen jälkeen kun alusta on jätetty yksi tai kaksi termiä pois.
Pätevätkö ehdot seuraaville sarjoille?
Perusidea
Tämän tehtävän kikassa muodostetaan sarjan summalle hyvin yksinkertainen ylälikiarvo ja sievennetään se mahdollisimman yksinkertaiseen `O`-muotoon. Sitten muodostetaan yksinkertainen alalikiarvo ja sievennetään se mahdollisimman yksinkertaiseen `Omega`-muotoon. Lopuksi katsotaan, tuliko samat muodot. Jos tuli samat, tulos on sarjan summalle pätevä `Theta`-merkintä. Jollei tullut samat, menetelmä epäonnistui. Yleensä tulee samat.
Ylälikiarvo
Alalikiarvo
 Sarjan summalle saataisiin alalikiarvo kertomalla ensimmäinen termi termien
määrällä, mutta se on yleensä eri muotoa kuin ylälikiarvo, joten näin
menetellen ei päästä tavoitteeseen.
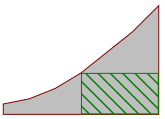
Melkein aina tavoitteeseen vievä alalikiarvo saadaan käyttämällä keskimmäistä
termiä alalikiarvona sarjan loppuosan jokaiselle termille ja jättämällä
alkuosan termit pois.
Keskimmäinen termi on tästä syystäkasvavuusoletuksen vuoksi pätevä alalikiarvo
loppuosan termeille.
Lupa jättää alkuosan termit pois tulee siitä, että …Ne ovat oletuksen `f(1) >= 0` ja kasvavuusoletuksen mukaan
ei-negatiivisia.
Niille saa siis käyttää alalikiarvona nollaa.
Niinpä niiden summan alalikiarvoksi tulee
`0``+``0``+``...``+``0``=``0`.
Sarjan summalle saataisiin alalikiarvo kertomalla ensimmäinen termi termien
määrällä, mutta se on yleensä eri muotoa kuin ylälikiarvo, joten näin
menetellen ei päästä tavoitteeseen.
Melkein aina tavoitteeseen vievä alalikiarvo saadaan käyttämällä keskimmäistä
termiä alalikiarvona sarjan loppuosan jokaiselle termille ja jättämällä
alkuosan termit pois.
Keskimmäinen termi on tästä syystäkasvavuusoletuksen vuoksi pätevä alalikiarvo
loppuosan termeille.
Lupa jättää alkuosan termit pois tulee siitä, että …Ne ovat oletuksen `f(1) >= 0` ja kasvavuusoletuksen mukaan
ei-negatiivisia.
Niille saa siis käyttää alalikiarvona nollaa.
Niinpä niiden summan alalikiarvoksi tulee
`0``+``0``+``...``+``0``=``0`.
Tarkastellaan ensin tilannetta, jossa ensimmäinen termi on `f(1)` ja viimeinen `f(n)`. Jos termejä on pariton määrä, keskimmäinen termi on `f((n+1)/2)` ja siitä alkavassa loppuosassa on `(n+1)/2` termiä. Jälkimmäistä voidaan arvioida alaspäin lausekkeella `n/2`, ja kasvavuuden ansiosta edellistä voidaan arvioida alaspäin lausekkeella `f(n/2)`. Näin saadaan alalikiarvo `n/2 f(n/2)`, joka on helpompaa muotoa kuin muut vaihtoehdot.
Helpon muotoista alalikiarvoa `n/2 f(n/2)` voidaan käyttää myös jos termejä on parillinen määrä. Silloin keskikohta osuu termien `f(n/2)` ja `f(n/2+1)` väliin. Termistä `f(n/2+1)` termiin `f(n)` on `n/2` termiä. Kasvavuusoletuksen vuoksi niiden alalikiarvona voi käyttää `f(n/2)`. Lauseketta `n/2 f(n/2)` voidaan siis käyttää aina, riippumatta siitä, onko `n` parillinen vai pariton.
Jos ensimmäinen termi onkin `f(0)` ja `f(0)``>=``0`, voimme silti käyttää lauseketta `n/2 f(n/2)`, koska …Silloin `f(0)``+``f(1)``+``...``+``f(n)``>=``f(1)``+``...``+``f(n)``>=``n/2 f(n/2)`.
Tulosten yhdistäminen
Harjoitellaan!
Entä jos pitääkin laskea `log 1``+``...``+``log (n-1)`? Sehän on `(log 1``+``...``+``log n) - log n`, missä sulkujen sisältö tutkittiin edellä. Edellä saatu vastaus on enemmän merkitsevää muotoa kuin `log n`, joten `-log n` voidaan jättää pois. Saadaan siis sama vastaus kuin edellä. Helppoa! Muista kuitenkin, että vähemmän merkitsevän termin saa jättää pois vain kiinteän määrän kertoja. On oikein päätellä, että koska `log 1` ja `log 2` ovat vakioita ja siksi merkitsevät vähemmän kuin `log n`, ne saa jättää pois ja siis
`Theta(log 1``+``...``+``log n)``=``Theta(log 3``+``...``+``log n)` .
Ei kuitenkaan olisi oikein toistaa tämä päättely kolmen pisteen yli ja todeta, että
`Theta(log 1``+``...``+``log n) color(red)(= Theta(log n))` .
Käsitellään seuraavaksi hieman hankalampi tapaus:
`5 sqrt(1)``+``7 sqrt(2)``+``...``+``(2n-1)sqrt(n-2)`.
Kikka ei toimi aina
Ne eivät ole samaa muotoa. Potenssilaskun kantaluku ei ole vakiokerroin, jonka saa poistaa tai vaihtaa ykköseksi `Theta`-merkintää käytettäessä. (Jos saisi, voisimme johtaa `2^n color(red)(= Theta(1^n) = Theta(1))` eli varsin nopeasti kasvava funktio olisi samaa muotoa kuin funktio, joka ei kasva lainkaan!)
Tarkan muodon vertaaminen edellä johdettuihin ylä- ja alalikiarvoihin kertoo, että kumpikin likiarvo on huono. Tässä tapauksessa syynä on se, että sarjan termit kasvavat varsin nopeasti. Tällaisia sarjoja esiintyy algoritmien analyysissa, mutta silloin algoritmi on ainakin joillakin suurilla syötteillä toivottoman hidas. Yleensä pyritään löytämään nopeampia algoritmeja jos mahdollista. Siksi tämän tehtävän kikka toimii käytännön algoritmien analyysissa melkein aina.
Lopuksi
Edellä käytetty ylälikiarvon muodostamistapa on hyvin yksinkertainen ja kannattaa osata. Myös alalikiarvon muodostamistapa kannattaa muistaa, sillä se on laajasti käyttökelpoinen. Se oli seuraava:
- Sarja jaettiin kahtia pieniin ja suuriin termeihin.
- Jokaisen pienen termin alalikiarvona käytettiin nollaa.
- Jokaisen suuren termin alalikiarvona käytettiin keskimmäistä termiä.