`|a| = {(-a, sf", kun " a < 0),(a, sf", kun " a >= 0):}`

Teh­tä­vä:
It­seis­ar­vo

Ly­hyt Math­Check-oh­je (uu­teen vä­li­leh­teen)

It­seis­ar­von kä­si­te

Reaa­li­lu­vuil­la it­seis­ar­vo ku­vaa lu­vun etäi­syyt­tä nol­las­ta. Yk­sin­ker­tai­sis­sa ti­lan­teis­sa it­seis­ar­von voi aja­tel­la vain pois­ta­van mii­nus­mer­kin lu­vun edes­tä, mut­ta han­ka­lam­mis­sa tä­mä ajat­te­lu­ta­pa voi joh­taa har­haan. Kai­kil­la reaa­li­lu­vuil­la `x` pi­tää paik­kan­sa, et­tä `|x| = |-x|`, mut­ta kek­sit­kö reaa­li­lu­vun, jol­la `|-x| = x` ei ole­kaan to­si? vas­tausMi­kä ta­han­sa ne­ga­tii­vi­nen lu­ku. Va­li­taan esi­mer­kik­si `x = -2`, jol­loin `|-x| = |-(-2)| = |2| = 2 != -2`.

It­seis­ar­voa voi­daan hyö­dyn­tää myös las­ket­taes­sa kah­den reaa­li­lu­vun etäi­syyt­tä toi­sis­taan. Tie­dät­kö mi­ten? vih­jeMi­ten las­ket lu­ku­jen `4` ja `3` vä­li­sen etäi­syy­den? En­tä lu­ku­jen `-2` ja `7`, tai lu­ku­jen `sqrt 10` ja `pi`? On­ko lu­ku­jen jär­jes­tyk­sel­lä vä­liä? Kek­sit­kö kaa­van, jo­ta käyt­tä­mäl­lä ei ole vä­liä kum­pi lu­ku on isom­pi ja kum­pi pie­nem­pi? vas­tausLu­ku­jen `x` ja `y` vä­li­nen etäi­syys on `|x-y|`.

Tar­kas­tel­laan it­seis­ar­vo­lau­se­ket­ta `|4x - 3|`. Hah­mot­te­le aluk­si it­se pa­pe­ril­le, mil­tä sen ku­vaa­ja näyt­tää, ja ver­taa sit­ten ku­vaa­si tä­hän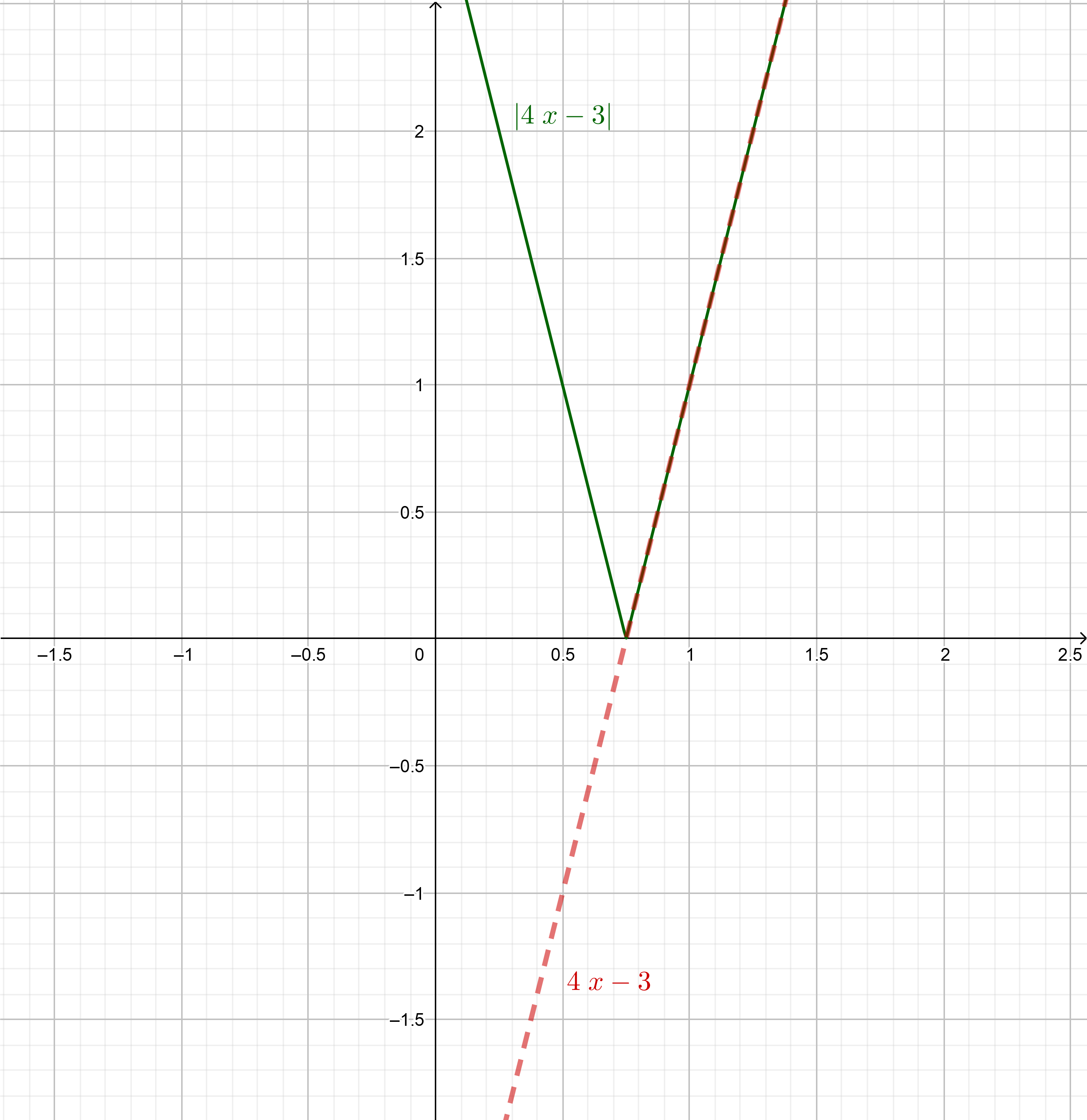. Hah­mot­te­le sa­maan ku­vaan lau­sek­keen `|3 - 4x|` ku­vaa­ja. Mi­tä huo­maatKu­vaa­jat ovat sa­mat.?

It­seis­ar­vo­ja si­säl­tä­vä lau­se­ke voi­daan il­mais­ta myös il­man it­seis­ar­vo­merk­ke­jä. Sil­loin hyö­dyn­ne­tään sa­maa it­seis­ar­von mää­ri­tel­mää, jo­ka on ker­rot­tu luen­to­ma­te­riaa­leis­sa­kin:

`|a| = {(-a, sf", kun " a < 0),(a, sf", kun " a >= 0):}`

It­seis­ar­von mää­ri­tel­män mu­kaan aiem­pi esi­merk­ki voi­daan siis kir­joit­taa

`|4x - 3| = -(4x - 3)`   , kun   `4x - 3 < 0`.

ja

`|4x - 3| = 4x - 3`   , kun   `4x - 3 >= 0`

Har­joi­tel­kaam­me tä­tä! Säi­ly­tä vas­tauk­se­si, nii­tä tar­vi­taan pian. Al­la on käy­tet­ty ru­mem­paa ma­te­ma­tii­kan esi­tys­ta­paa kuin edel­lä sik­si, et­tä ru­mas­ta esi­tys­ta­vas­ta voi maa­la­ta ja ko­pioi­da. Se hel­pot­taa vas­taus­ten kir­joit­ta­mis­ta. Ru­ma esi­tys­ta­pa myös vä­hen­tää vep­pi­si­vun hyp­pi­mis­tä ja pomp­pi­mis­ta kun si­vu la­da­taan, ja no­peut­taa vas­taus­ruu­dus­ta toi­seen siir­ty­mis­tä ta­bu­laat­to­ri­näp­päi­mel­lä.

ok_text Oi­kein! arithmetic f_nodes 6 hide_expr -(2x+8) = |2x + 8| = , kun end_of_answer arithmetic f_nodes 5 hide_expr 2x+8 = < 0
tai

ja

ok_text Oi­kein! arithmetic f_nodes 5 hide_expr 2x+8 = |2x + 8| = , kun end_of_answer arithmetic f_nodes 5 hide_expr 2x+8 = ≥ 0
tai

Vie­lä toi­nen! Säi­ly­tä tä­män­kin vas­tauk­se­si.

ok_text Oi­kein! arithmetic f_nodes 6 hide_expr -(18-6x) = |18 − 6x| = , kun end_of_answer arithmetic f_nodes 5 hide_expr 18-6x = < 0
tai

ja

ok_text Oi­kein! arithmetic f_nodes 5 hide_expr 18-6x = |18 − 6x| = , kun end_of_answer arithmetic f_nodes 5 hide_expr 18-6x = ≥ 0
tai

Toi­si­naan on hyö­dyl­lis­tä sie­ven­tää vä­hän pi­dem­mäl­le, niin et­tä eh­to on rat­kais­tu muut­tu­jan suh­teen:

`|4x - 3| = 4x - 3`   , kun   `x >= 3/4`

ja

`|4x - 3| = 3 - 4x`   , kun   `x < 3/4`.

Näin on eri­tyi­ses­ti sil­loin, kun it­seis­ar­vo­merk­ke­jä on kak­si tai enem­män. Otam­me esi­mer­kik­si 3|2x + 8| − |18 − 6x|. Sie­ven­nä it­seis­ar­vot pois­ta­mal­la syn­ty­vä lau­se­ke. Ken­ties kan­nat­taa kir­joit­taa se en­sin sie­ven­tä­mät­tö­mä­nä ja kli­ka­ta vas­taus­nap­pia, jot­ta nä­ki­sit, me­ni­kö sii­hen as­ti oi­kein. Sit­ten voit li­sä­tä pe­rään = ja sie­ven­ne­tyn vas­tauk­sen. Tar­vit­taes­sa voit kir­joit­taa usei­ta vä­li­vai­hei­ta =-mer­kin avul­la.

ok_text Oi­kein! arithmetic f_nodes 6 hide_expr -12x-6 = kun 2x + 8 < 0 ∧ 18 − 6x < 0
tai

ok_text Oi­kein! arithmetic f_nodes 2 hide_expr 0x-42 = kun 2x + 8 < 0 ∧ 18 − 6x ≥ 0
tai

ok_text Oi­kein! arithmetic f_nodes 1 hide_expr 0x+42 = kun 2x + 8 ≥ 0 ∧ 18 − 6x < 0
tai

ok_text Oi­kein! arithmetic f_nodes 5 hide_expr 12x+6 = kun 2x + 8 ≥ 0 ∧ 18 − 6x ≥ 0
tai

Yl­lä ole­vas­ta on han­ka­la hah­mot­taa, mil­lä x:n ar­voil­la mi­kä­kin lau­se­ke on voi­mas­sa. Sik­si sie­ven­nä jo­kai­nen eh­to mah­dol­li­sim­man sel­keään muo­toon. Ylin ja alin ovat vai­keim­mat, jo­ten älä aloi­ta niil­lä.

ok_text Oi­kein! real_logic solve_all f_nodes 1 2x + 8 < 0 /\ 18 - 6x < 0 <=>
tai

ok_text Oi­kein! real_logic solve_all f_nodes 4 2x + 8 < 0 /\ 18 - 6x >= 0 <=>
tai

ok_text Oi­kein! real_logic solve_all f_nodes 3 2x + 8 >= 0 /\ 18 - 6x < 0 <=>
tai

Vih­je`x < c ^^ x >= d` voi­daan esit­tää myös `d <= x < c`. komp­lek­si­suu­den pie­nen­tä­mi­sek­si
ok_text Oi­kein! real_logic solve_all f_nodes 6 2x + 8 >= 0 /\ 18 - 6x >= 0 <=>
tai

Kaik­kiaan saa­tiin (luet­te­le ta­pauk­set x:n kas­va­vas­sa jär­jes­tyk­ses­sä):

• ok_text Oi­kein! arithmetic f_nodes 2 hide_expr 0x-42 = 3|2x + 8| − |18 − 6x| = , kun end_of_answer real_logic f_nodes 4 hide_expr x < -4 <=>
• end_of_answer arithmetic f_nodes 5 hide_expr 12x+6 = 3|2x + 8| − |18 − 6x| = , kun end_of_answer real_logic f_nodes 6 hide_expr -4 <= x <= 3 <=>
• end_of_answer arithmetic f_nodes 1 hide_expr 0x+42 = 3|2x + 8| − |18 − 6x| = , kun end_of_answer real_logic f_nodes 3 hide_expr 3 < x <=>

tai

Täs­tä saat funk­tion ku­vaa­jan. Voit myö­hem­min vaih­taa sii­hen oman funk­tion, jos ha­luat tar­kas­tel­la si­tä. x-ak­se­li al­kaa ja päät­tyy pik­ku­laa­ti­kois­sa ole­vis­ta koh­dis­ta.
draw_function -10 10 ;
3|2x + 8| - |18 - 6x| tai

It­seis­ar­vo­yh­tä­löi­tä

Mi­ten mää­ri­tel­mää hyö­dyn­ne­tään yh­tä­löi­den rat­kai­se­mi­ses­sa? Ote­taan esi­mer­kik­si `|4x - 3| = 5`. Math­Checkiä tar­kas­tus­apu­na käyt­täen se voi­daan rat­kais­ta mo­nel­la ta­val­la. Seu­raa­vak­si ku­vat­ta­va ta­pa on eh­kä aloit­te­li­jal­le suo­si­tel­ta­vin, kos­ka se muo­dos­taa hy­vän komp­ro­mis­sin kir­joit­ta­mis­vai­van ja Math­Checkin an­ta­man tar­kas­tus­avun vä­lil­le.

ok_text Oi­kein! real_logic f_nodes 10 solve_all |4x - 3| = 5 <=> 4x - 3 < 0 /\ -(4x - 3) = 5 \/ 4x - 3 >= 0 /\ 4x - 3 = 5 subproof assume 4x - 3 < 0; original <=> -(4x - 3) = 5 <=> 4x - 3 = -5 <=> 4x = -2 <=> x = -1/2 subend subproof assume 4x - 3 >= 0; original <=> 4x - 3 = 5 <=> 4x = 8 <=> x = 2 subend /*Tar­kas­tus: ovat­ko saa­dut juu­ret vaa­di­tuil­la vä­leil­lä?*/ /*Kun `x=-1/2` niin `4x-3 = -2-3 = -5 < 0`, siis `-1/2` on pä­te­vä juu­ri.*/ /*Kun `x=2` niin `4x-3 = 8-3 = 5 >= 0`, siis `2` on pä­te­vä juu­ri.*/ original <=> x = -1/2 \/ x = 2
tai
Klik­kaa nap­pia ja lue Math­Checkin pa­lau­te. Seu­raa­vas­sa on se­los­tet­tu jo­kai­nen vai­he. Var­mis­ta, et­tä ym­mär­rät ne.

En­sim­mäi­sel­lä vas­taus­ri­vil­lä it­seis­ar­vo­mer­kit on pois­tet­tu ku­ten edel­lä on ku­vat­tu. Syn­ty­vät kak­si ta­paus­ta on ero­tet­tu toi­sis­taan ope­raat­to­ril­la ∨, ja ta­pauk­sen eh­to ja yh­tä­lö on yh­dis­tet­ty ope­raat­to­ril­la ∧. Ru­ti­noi­tu­nut sie­ven­tä­jä voi jät­tää tä­män ri­vin kir­joit­ta­mat­ta. Aloit­te­li­ja voi hyö­tyä sen tuot­ta­mas­ta li­sä­tar­kas­tuk­ses­ta.

Tar­kas­tus var­mis­taa vain, et­tä ri­vi on to­si täs­mäl­leen niil­lä x:n ar­voil­la, joil­la al­ku­pe­räi­nen yh­tä­lö to­teu­tuu. Sik­si se sal­lii vir­hei­tä var­sin­kin eh­dois­sa, mut­ta vain sel­lai­sia, jot­ka ei­vät vai­ku­ta lop­pu­tu­lok­seen. Ko­kei­le tä­tä vaih­ta­mal­la en­sim­mäi­ses­sä assume-osas­sa 0:n pai­kal­le en­sin 5 ja sit­ten 6. Mik­si tu­los on sel­lai­nen kuin on? Vas­tausAl­ku­pe­räi­nen yh­tä­lö on to­si jos ja vain jos `x = -1/2` tai `x = 2`. Ta­pauk­sen yh­tä­lö `-(4x - 3) = 5` on to­si jos ja vain jos `x = -1/2`.

Kun assume-osas­sa an­net­tu ra­ja on 0 tai 5, niin 2 ei to­teu­ta ole­tus­ta, jo­ten si­tä ei ote­ta huo­mioon. Niin­pä se­kä al­ku­pe­räi­nen et­tä ta­pauk­sen yh­tä­lö to­teu­tu­vat täs­mäl­leen sa­moil­la tar­kas­tel­ta­vil­la x:n ar­voil­la. Yh­tä­löt ovat sil­loin lo­gii­kan nä­kö­kul­mas­ta yh­tä­pi­tä­vät.

Kun assume-ra­ja on 6, myös `x = 2` ote­taan huo­mioon. Täl­löin, kun `x = 2`, niin al­ku­pe­räi­nen yh­tä­lö on to­si ja ta­pauk­sen yh­tä­lö epä­to­si, jo­ten yh­tä­löt ei­vät ole yh­tä­pi­tä­vät.

Seu­raa­vil­la kol­mel­la ri­vil­lä rat­kais­taan ta­paus < 0. Osuus assume 4x - 3 < 0; ra­joit­taa tar­kas­tuk­sen ta­pauk­sen mu­kai­siin x:n ar­voi­hin, ja original <=> käs­kee tar­kas­ta­maan, et­tä rat­kais­ta­va yh­tä­lö täs­mää al­ku­pe­räi­seen yh­tä­löön. Ne ei­vät ole vält­tä­mät­tö­miä, mut­ta ovat hyö­dyk­si pal­jas­ta­mal­la he­ti ta­pauk­sia, jois­sa it­seis­ar­vo­mer­kit on pois­tet­tu vää­rin. Il­man nii­tä voi käy­dä niin, et­tä vir­he pal­jas­tuu vas­ta lo­puk­si, jol­loin tu­lee rat­kais­tua vää­rä yh­tä­lö ja si­ten teh­tyä tur­haa työ­tä.

Seu­raa­vil­la kol­mel­la ri­vil­lä rat­kais­taan ta­paus ≥ 0.

Tar­kas­tus, täyt­tää­kö kum­pi­kin saa­tu juu­ri ta­pauk­sen­sa eh­don, on jä­tet­ty pääs­sä teh­tä­väk­si. Se ei tar­vit­se ko­neel­lis­ta tar­kas­tus­ta, kos­ka se on help­poa, ja sii­nä mah­dol­li­ses­ti teh­ty vir­he pal­jas­tuu lo­pul­li­sen vas­tauk­sen koh­dal­la. Opet­ta­ja esit­ti sen kom­ment­ti­na ha­vain­nol­li­suu­den vuok­si, mut­ta opis­ke­li­jan ei tar­vit­se kir­joit­taa si­tä.

Vii­mei­sel­lä ri­vil­lä on lo­pul­li­nen vas­taus. Osuus original <=> ker­too, et­tä se on al­ku­pe­räi­sen yh­tä­lön vas­taus.

Yh­tä­löä rat­kais­taes­sa tar­kas­tel­laan siis erik­seen ti­lan­teet, jois­sa it­seis­ar­von si­säl­lä ole­va lau­se­ke on po­si­tii­vi­nen tai nol­la, ja ti­lan­teet, jois­sa se on ne­ga­tii­vi­nen. Nä­mä yh­dis­tä­mäl­lä saa­daan lo­pul­li­nen vas­taus. Kat­so vie­lä tä­mä ku­va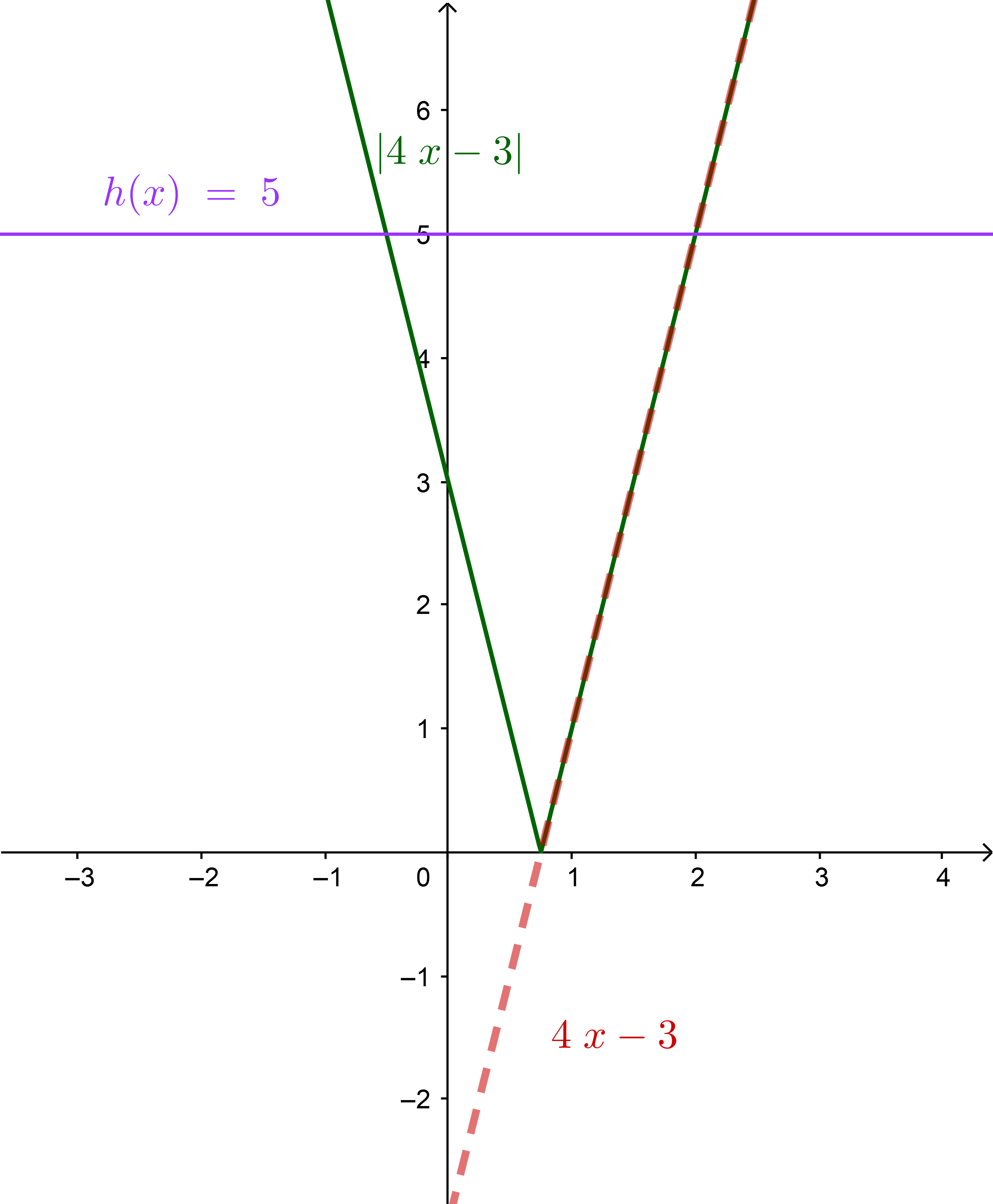, jos­sa aiem­min piir­ret­tyyn ku­vaan on li­sät­ty suo­ra `y = 5` ja jos­ta sik­si yh­tä­lön juu­ret nä­ky­vät.

Rat­kai­se seu­raa­vat kol­me it­seis­ar­vo­yh­tä­löä. Hah­mot­te­le jo­kai­ses­ta myös ku­va pa­pe­ril­le ja mie­ti, mi­ten yh­tä­lön rat­kai­su nä­kyy ku­vas­sa. Älä kui­ten­kaan pe­rus­ta rat­kai­sua­si ku­vaan tai tee pää­tel­miä yk­sin sen pe­rus­teel­la. Pa­pe­rin si­jaan voit käyt­tää edel­lä ol­lut­ta ku­vaa­jan­piir­to­ruu­tua. Kir­joi­ta =-mer­kin pai­kal­le ; (se tar­koit­taa, et­tä piir­rä sa­maan ku­vaan kak­si ku­vaa­jaa). Voit pyyh­kiä val­miik­si kir­joi­te­tun mer­kin ⇔ pois, jos ha­luat aloit­taa subproof-loh­kol­la.

ok_text Oi­kein! real_logic f_nodes 6 solve_all |x| = 5x + 2
<=>
tai

ky­sy­mys rat­kai­sus­taTäl­lä yh­tä­löl­lä on vain yk­si juu­ri. Mik­si las­ke­mal­la saa­tiin mah­do­ton juu­ri `-1/2` (ku­vas­ta voi ol­la apua)? vas­tausKu­vas­sa on vih­reäl­lä kat­ko­vii­val­la `x` ja `-x`. Haa­mu­juu­ri syn­tyy suo­rien `y=x` ja `y=5x+2` leik­kaus­pis­tee­seen. Siel­lä `x = 5x+2` mut­ta `|x| != 5x+2`, kos­ka `|x| > 0` mut­ta `5x+2 < 0`. Tä­mä on esi­merk­ki juu­res­ta, jo­ka ei to­teu­ta ta­pauk­sen­sa eh­toa. Edel­lä käs­ket­tiin hy­lä­tä sel­lai­set juu­ret.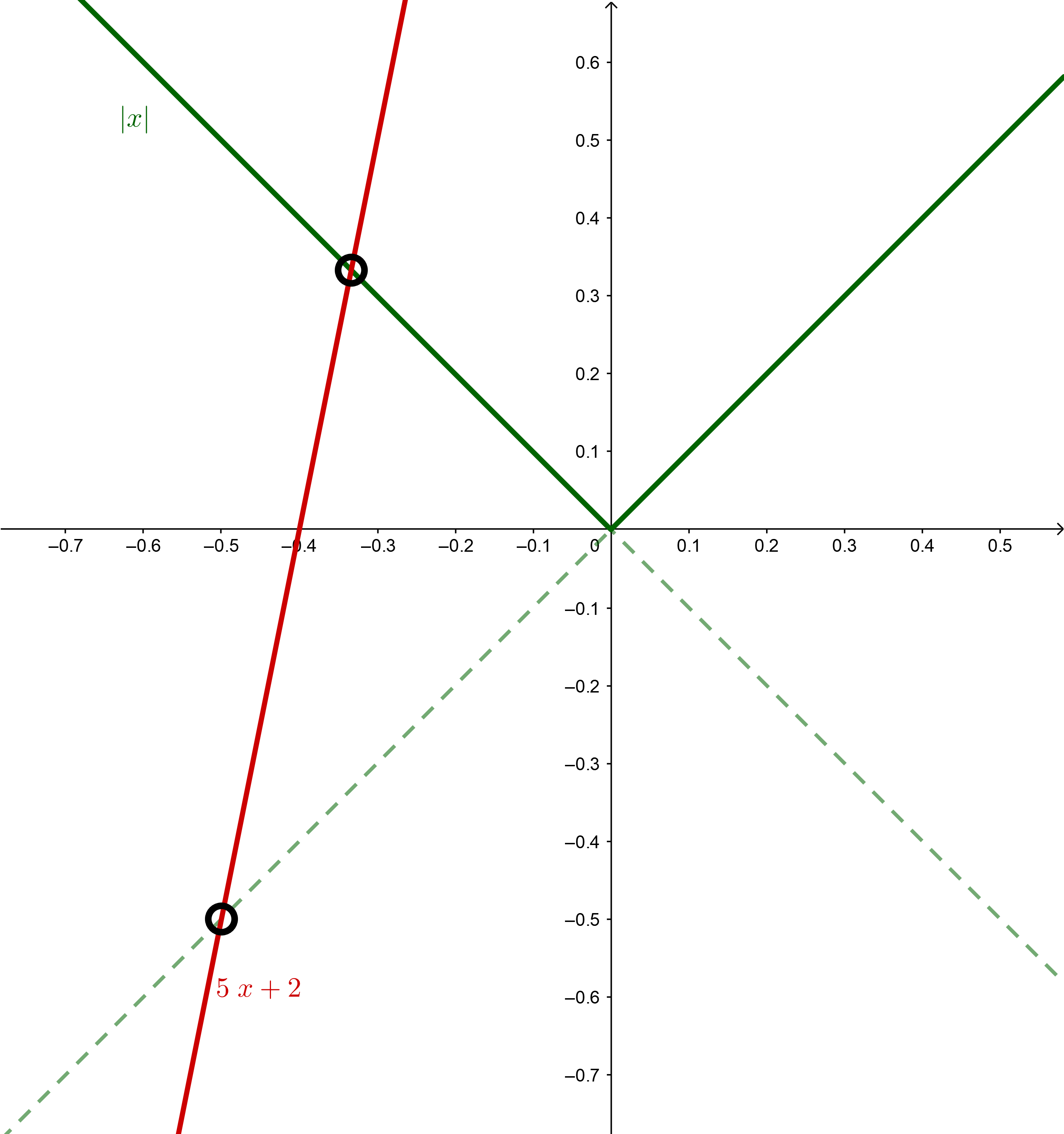

ok_text Oi­kein! real_logic f_nodes 15 solve_all |4x + 6| = -2x + 3
<=>
tai

ok_text Oi­kein! /*Täs­tä ai­na­kin kan­nat­taa piir­tää ku­va!*/ real_logic f_nodes 1 solve_all |8 - 4x| = x - 3
<=>
tai

Tä­mä rat­keaa hy­vin vä­häl­lä työl­lä, jos si­nul­la on hy­vä muis­ti tai ker­taat edel­tä tar­peek­si.
ok_text Oi­kein! real_logic f_nodes 10 solve_all |3-4x| = 5
<=>
tai

En­täs jos it­seis­ar­vo­ja on usei­ta? Mi­ten rat­kais­taan esi­mer­kik­si yh­tä­lö `|x + 4| = |3x+6|` tai yh­tä­lö `|x+3| = |4-2x| - 1`? Ne voi­daan rat­kais­ta ihan sa­mal­la ideal­la kuin aiem­mat­kin yh­tä­löt, mut­ta niis­sä pi­tää pi­tää pää kyl­mä­nä kos­ka ta­pauk­sia tu­lee usei­ta.

Tar­kas­tel­laan en­sin yh­tä­löä `|x + 4| = |3x+6|`. Aloi­ta piir­tä­mäl­lä ku­va. Älä tee pää­tel­miä ku­vas­ta, mut­ta yri­tä hah­mot­taa mi­ten teh­tä­vät las­kut ja päät­te­lyt nä­ky­vät sii­nä.

Va­sem­mal­la puo­lel­la ole­van it­seis­ar­von si­säl­lä ole­va lau­se­ke `x + 4` saa ar­von `0` kun `x = -4`. Siis­pä kun `x >= -4` niin `|x + 4| = x + 4` ja kun `x < -4` niin `|x + 4| = -x - 4`.

Oi­keal­la puo­lel­la ole­van it­seis­ar­von si­säl­lä ole­va lau­se­ke `3x+6` puo­les­taan saa ar­von `0` kun `x = -2`. Siis­pä kun `x >= -2` niin `|3x+6| = 3x+6` ja kun `x < -2` niin `|3x+6| = -3x-6`.

Näis­tä tu­lee kaik­kiaan nel­jä yh­dis­tel­mää. Sie­ven­nä ne:

`x < -4 ^^ x < -2 hArr` ok_text Oi­kein! real_logic solve_all f_nodes 4 x < -4 /\ x < -2 <=>
tai

`x < -4 ^^ x >= -2 hArr` ok_text Oi­kein! real_logic solve_all f_nodes 1 x < -4 /\ x >= -2 <=>
tai

`x >= -4 ^^ x < -2 hArr` ok_text Oi­kein! real_logic solve_all f_nodes 7 x >= -4 /\ x < -2 <=>
tai

`x >= -4 ^^ x >= -2 hArr` ok_text Oi­kein! real_logic solve_all f_nodes 4 x >= -4 /\ x >= -2 <=>
tai

Mil­le näis­tä ta­pauk­sis­ta ei tar­vit­se jat­kos­sa teh­dä mi­tään, ja mik­si? vas­tausTa­pauk­sel­le `x < -4 ^^ x >= -2`, kos­ka sel­lai­sia lu­ku­ja ei ole, jot­ka oli­si­vat al­le `-4` mut­ta sa­mal­la vä­hin­tään `-2`.

Seu­raa­vak­si nä­mä yk­sit­täi­sis­tä it­seis­ar­vo­lau­sek­keis­ta saa­dut tie­dot täy­tyy yh­dis­tää yh­tä­lön `|x + 4| = |3x+6|` rat­kai­se­mi­sek­si.

Täy­tä al­la ole­vien pien­ten vas­taus­laa­ti­koi­den en­sim­mäi­seen sa­rak­kee­seen ne ra­jat, jois­sa muut­tu­jaa `x` kul­la­kin ri­vil­lä tar­kas­tel­laan. Kol­man­teen sa­rak­kee­seen tu­lee rat­kais­ta­van yh­tä­lön va­sen puo­li it­seis­ar­vot pu­ret­tu­na an­net­tu­jen ra­jo­jen mu­kai­ses­ti. Vii­den­teen sa­rak­kee­seen täy­te­tään yh­tä­lön oi­kea puo­li vas­taa­vas­ti. Osa laa­ti­kois­ta on täy­tet­ty jo val­miik­si.

Vas­taus­laa­tik­ko on jaet­tu useaan osaan, kos­ka näin on mah­dol­lis­ta pal­jas­taa osa rat­kai­sus­ta, mut­ta jät­tää sa­mal­la osa it­se pää­tel­tä­väk­si. Math­Check kä­sit­te­lee laa­ti­koi­hin syö­te­tyt vas­tauk­set kuin ne oli­si kir­joi­tet­tu yh­teen laa­tik­koon aiem­pien koh­tien ta­paan.
ok_text Oi­kein! real_logic f_nodes 50 |x + 4| = |3x+6| <=>
x < -4/\-x-4=-3x-6\/
/\x+4=\/
/\=
tai

Vie rat­kai­su lop­puun.
ok_text Oi­kein! real_logic f_nodes 13 solve_all |x + 4| = |3x+6| <=>
tai

Rat­kai­se sa­maan ta­paan yh­tä­lö `|x+3| = |4-2x| - 1`:
ok_text Oi­kein! real_logic f_nodes 7 solve_all |x+3| = |4-2x| - 1
<=>
tai

It­seis­ar­vo­epä­yh­tä­löi­tä

It­seis­ar­vo­yh­tä­löl­lä on tyy­pil­li­ses­ti muu­ta­ma juu­ri. On ole­mas­sa eri­kois­ti­lan­tei­ta, jois­sa it­seis­ar­vo­yh­tä­lön rat­kai­su­na on vä­li. Kek­sit­kö sel­lai­sen? vas­tausTä­mä lie­nee yk­sin­ker­tai­sin: `|x| = x`

Epä­yh­tä­löi­den rat­kai­sut puo­les­taan muo­dos­tu­vat usein yh­des­tä tai useas­ta vä­lis­tä. Rat­kai­se­mi­nen ete­nee sa­maan ta­paan kuin yh­tä­löi­den­kin ta­pauk­ses­sa. Ne­ga­tii­vis­ten ker­toi­mien kans­sa täy­tyy kui­ten­kin ol­la tark­ka­na. Kun epä­yh­tä­lön mo­lem­mat puo­let ker­ro­taan tai jae­taan ne­ga­tii­vi­sel­la lu­vul­la, sen suun­ta vaih­tuu. Tar­kas­tel­laan en­sim­mäis­tä esi­merk­kiä:

Rat­kai­se `|3x - 6| <= 6`:
ok_text Oi­kein! real_logic f_nodes 5 solve_all |3x - 6| <= 6
<=>
tai

Edel­li­sen koh­dan rat­kai­su on sul­jet­tu vä­li. Sul­jet­tu vä­li on vä­li, jon­ka pää­te­pis­teet kuu­lu­vat vä­lil­le. Avoi­mel­la vä­lil­lä pää­te­pis­teet ei­vät kuu­lu vä­lil­le, ku­ten esi­mer­kik­si ta­pauk­ses­sa `2 < x < 5`. Puo­li­avoi­mel­la vä­lil­lä toi­nen pää­te­pis­te kuu­luu vä­lil­le, ja toi­nen ei.

Seu­raa­vis­sa koh­dis­sa tu­lee vas­taan eri­lai­sia rat­kai­su­jouk­ko­ja. Ku­ten aiem­min­kin, ku­van piir­tä­mi­ses­tä voi ol­la hyö­tyä rat­kai­su­jen hah­mot­ta­mi­ses­sa (mut­ta se ei kor­vaa koh­dan rat­kai­se­mis­ta las­kien).

Rat­kai­se `|2x| > 1-x`:
ok_text Oi­kein! real_logic f_nodes 10 solve_all |2x| > 1-x
<=>
tai

Rat­kai­se `|8+4x| > 3x - 4`:
ok_text Oi­kein! real_logic f_nodes 1 solve_all |8+4x| > 3x - 4
<=>
tai

Rat­kai­se `|x| > 1/2 x`:
ok_text Oi­kein! real_logic f_nodes 7 b_nodes 3 solve_all |x| > 1/2 x
<=>
tai

Seu­raa­vis­sa voit eh­kä hyö­dyn­tää jo­ta­kin aiem­paa koh­taa.

Rat­kai­se `|x + 4| < |3x+6|`:
ok_text Oi­kein! real_logic f_nodes 13 solve_all |x + 4| < |3x+6|
<=>
tai

Rat­kai­se `|x+3| + 1 >= |4-2x|`:
ok_text Oi­kein! real_logic f_nodes 5 solve_all |x+3| + 1 >= |4-2x|
<=>
tai

Ede­tään lo­puk­si vai­heit­tain yh­tä­löön, jo­ka voi näyt­tää vai­keal­ta, mut­ta on hy­vin help­po.

Rat­kai­se `|a| <= 0`:
ok_text Oi­kein! real_logic f_nodes 3 solve_all |a| <= 0
<=>
tai

Rat­kai­se `|a| + 1 <= 0`:
ok_text Oi­kein! real_logic f_nodes 1 solve_all |a|+1 <= 0
<=>
tai

Rat­kai­se `|a| + |b| <= 0`:
ok_text Oi­kein! real_logic f_nodes 7 b_nodes 5 solve_all |a|+|b| <= 0
<=>
tai