Tehtävä:
Hajautustaulun muistinkäyttö
Lyhyt
MathCheck-ohje (uuteen välilehteen)
Hajautustaulu (hash table) on erittäin tehokas tietorakenne
silloin, kun tietoja tarvitsee lisätä, poistaa ja etsiä avaimen
perusteella, mutta ei tarvitse esimerkiksi selata suuruusjärjestyksessä.
Hajautustauluun kannattaa tallettaa esimerkiksi puhelinluettelo, josta
etsitään puhelinnumeroita nimien perusteella, mutta ei toisinpäin.
(Toisinpäin etsimistä varten voi olla toinen hajautustaulu.)
Tällöin avaimena on nimi.
Hyvin suunniteltu hajautustaulu on erittäin nopea eikä tuhlaa muistia.
Tässä tehtävässä tarkastellaan hajautustaulun muistinkulutusta.
Lista, johon kukin hyötykuorma sijoitetaan, valitaan
hajautusfunktion avulla.
Se ottaa avaimen ja tuottaa luvun väliltä 0, …, M − 1, missä M on
taulukon koko ja taulukkoa indeksoidaan nollasta alkaen.
Hajautusfunktio pyritään valitsemaan siten, että eri avaimet jakautuisivat
mahdollisimman tasaisesti eri listoihin.
Tällä tavoitellaan sitä, että pisin lista olisi mahdollisimman lyhyt.
Hajautustaulu on sitä hitaampi, mitä enemmän on pitkiä listoja ja mitä
pitempiä ne ovat.
Hyvän hajautusfunktion suunnittelu vaatii taitoa.
Emme käsittele sitä tässä yhteydessä tämän enempää, mutta mainittakoon, että
usein hajautusfunktioissa hyödynnetään modulaarista aritmetiikkaa.
Mitä suurempi taulukko valitaan, sitä lyhyempiä listoista keskimäärin
tulee, mutta sitä enemmän muistia taulukko itse vie.
Nykyaikaisissa tietokoneissa on tavallista, että tällaisissa tilanteissa
muistia annetaan 8 tavua kerrallaan.
Siksi oletamme, että osoitin vie 8 tavua ja yksi hyötykuorma (eli esimerkiksi
yksi nimi ja yksi puhelinnumero) vie 8h tavua.
Hajautustauluun on talletettava n hyötykuormaa.
Jos listan keskimääräinen pituus on p , niin M =
ok_text Oikein!
hide_expr f_nodes 3 n/p =
M avulla)
end_of_answer arithmetic
hide_expr f_nodes 13 8n/p + n(8h + 8) =
Klikkaamalla nappia saat käyrän, joka esittää muistin kulutusta p :n
funktiona muiden muuttujien realistisilla arvoilla n = 100 000 ja
h = 3.
hide_expr draw_function 0 10 0 10000000;
800000/p + 3200000
Käyrän perusteella vaikuttaa siltä, että
ok_text Teit oikeat valinnat!
only_no_yes_on hide_expr 0 = hide_expr 2
Kaiken tähänastisen tiedon valossa paras valinta p :n arvoksi on
only_no_yes_on ok_text Oikein!
hide_expr
Ei ole olemassa selvää rajaa sille, mitkä p :n arvot ovat pieniä, mitkä
keskisuuria ja mitkä suuria.
Koska hajautusfunktion laskenta vie oman aikansa, nopeuden kannalta hyviä ovat
ainakin ne p :n arvot, joille
ok_text Oikein!
modulo 23 hide_expr f_nodes 3 p ≤ 2 <=>
p 2
(kirjoita <= tai >= ).
Koska muistin kulutus ei voi olla negatiivinen ja koska 0 tavua vievä
hyötykuorma ei voi sisältää mitään hyödyllistä, voimme olettaa, että
end_of_answer
modulo 23 hide_expr f_nodes 3 h ≥ 1 <=>
Olettamalla mahdollisimman pieni hyötykuorma ja sijoittamalla p = 2
saadaan muistin kulutukseksi n :n funktiona
ok_text Oikein!
hide_expr f_nodes 3 8(n/2 + n + n) =
p
=
end_of_answer arithmetic
only_no_yes_on
/*Muistin kulutus on pienimmillään, kun listoja on yksi.
Silloin jokainen alkio on samassa listassa ja #<i#>p#</i#> on ko. listan
pituus.*/
hide_expr f_nodes 1 n =
end_of_answer arithmetic
only_no_yes_off
hide_expr f_nodes 5 16n + 8 =
Juuri lasketuista muistin kulutuksista edellinen on alle
only_no_yes_on ok_text Oikein!
hide_expr f_nodes 1 25 =
Jos listojen keskipituus p = ja hyötykuorma on yhä järkevässä
minimissään, niin muistia kuluu
ok_text Oikein!
hide_expr f_nodes 3 8(2n + n + n) =
end_of_answer arithmetic
only_no_yes_on
hide_expr f_nodes 1 100 =
Voidaan siis varsin huoletta antaa
p :n liikkua välillä
≤
p ≤ 2.
Muutkin
p :n arvot voivat olla käyttökelpoisia riippuen mm.
h :n
arvosta, hajautusfunktion laskemiseen kuluvasta ajasta ja siitä, kuinka
huolellisesti suorituskyky tarvitsee optimoida.
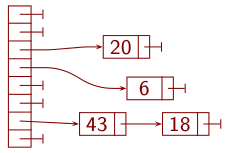 Oheinen kuva esittää hajautustaulua.
Siinä on taulukko, jonka alkiot ovat osoittimia.
Osoittimesta alkaa linkitetty lista, jonka kukin tietue sisältää yhden
hyötykuorman, siis esimerkiksi yhden nimen ja puhelinnumeron.
Kuvassa hyötykuormana on lukuja.
Tietueessa on myös osoitin listan seuraavaan alkioon.
Oheinen kuva esittää hajautustaulua.
Siinä on taulukko, jonka alkiot ovat osoittimia.
Osoittimesta alkaa linkitetty lista, jonka kukin tietue sisältää yhden
hyötykuorman, siis esimerkiksi yhden nimen ja puhelinnumeron.
Kuvassa hyötykuormana on lukuja.
Tietueessa on myös osoitin listan seuraavaan alkioon.