Tehtävä:
Rationaalilukujen joukko on nollamitallinen
Lyhyt MathCheck-ohje (uuteen välilehteen)
Tässä tehtävässä todistetaan kahdessa vaiheessa asia, joka on hyvin järjenvastainen, mutta silti totta. Saatava tulos selittää varsin pitkälle, miksi tietokoneet pärjäävät kokonaislukujen kanssa paljon paremmin kuin reaalilukujen kanssa. Matemaattisten taitojen osalta tehtävässä on kyse mielikuvana hahmotetun tilanteen esittämisestä ja käsittelemisestä yksinkertaisina lausekkeina ja suuruusjärjestysvertailuina.
Rationaalilukujen joukko on numeroituva
Tarvitsemme funktion f(m, n), joka tuottaa seuraavan kuvan mukaiset arvot, kun m ja n ovat positiivisia kokonaislukuja. Se saa siis peräkkäiset arvot, kun edetään vasemmalta vinosti alas oikealle ja aina alareunan kohdalla siirrytään vasempaan reunaan yhtä pykälää korkeammalle kuin edellisellä kerralla.
4 7 3 4 8 2 2 5 9 1 1 3 6 10 1 2 3 4
Jatkon kannalta riittää, että sellainen funktio on olemassa. Emme tule tarvitsemaan sen lauseketta. Oheinen kuva on itsessään pätevä todistus sille, että sellainen funktio on olemassa.
Funktion lausekkeen tutkiminen tarjoaa kuitenkin hyviä harjoituksia muun muassa argumenttiin sijoittamisesta ja sieventämisestä. Sitäpaitsi lausekkeen rakentamistapa on hyödyllinen muissa yhteyksissä, esimerkiksi kun halutaan tallettaa kaupunkien välisten etäisyyksien taulukko siten, että kukin etäisyys talletetaan vain yhteen suuntaan. Siksi osoitamme, että funktiollamme on alla oleva lauseke.
f(m, n) =− m + 1
(m + n)(m + n − 1) 2
Seuraavien kysymysten vastausruuduissa on varattu tilaa välivaiheelle ja lopputulokselle. Välivaihetta ei ole pakko kirjoittaa. Jos kirjoitat sen, laita sen ja lopputuloksen väliin =. Voit tarkastuttaa välivaiheen MathCheckillä ennen =-merkin ja lopputuloksen kirjoittamista.
Kuvan mukaan f(m, n):n arvo kasvaa yhdellä kun edetään yksi askel oikealle alas, mutta ollaksemme varmoja päättelemme f:n lausekkeesta, että näin todella on. Ilmaise m:n ja n:n (tai toisen tai ei kummankaan) funktiona, miten seuraavien lausekkeiden arvot muuttuvat, kun edetään yksi askel oikealle alas. Esimerkiksi jos arvelet, että arvo pienenee (n + 3):n verran, kirjoita -(n+3).
Tässäkin askeleessa f:n arvon pitää kasvaa yhdellä. On siis osoitettava, että f(uusi kohta) − f(1, n) = 1. Nytkin välivaiheille on varattu tilaa. Muistuttaakohan jompi kumpi tai molemmat kahdesta ylimmästä jotakin, johon olet vastannut jo aikaisemmin?
Olemme osoittaneet, että f(m, n) tuottaa alun kuvan mukaiset arvot.
Tästä seuraa välittömästi, että kaikki parit (m, n), missä m ∈ ℤ+ ja n ∈ ℤ+, saadaan jonoon joka alkaa mutta ei pääty. Jokainen pari on jonossa täsmälleen kerran, nimittäin kohdassa f(m, n).
Tässä vaiheessa on hyvä täsmentää, mitä matemaatikko tarkoittaa, kun hän puhuu päättymättömästä jonosta. Päättymättömän jonon paikat voidaan numeroida positiivisilla kokonaisluvuilla: paikka 1, paikka 2, paikka 3, …. Sellaisella luettelolla on alku muttei loppua. Jokaisen alkion perässä (siis oikealla puolella) on äärettömästi alkioita, mutta minkään alkion edessä (eli vasemmalla puolella) ei ole äärettömästi alkioita. Juuri sellaisen luettelon teimme äsken. Siinä alkion (m, n) paikka on f(m, n), ja varmistimme huolellisesti, että eri alkiot saivat eri paikat.
Joukon sanotaan olevan numeroituva, jos ja vain jos se on äärellinen tai sen alkiot voidaan asettaa päättymättömään jonoon. Muut joukot ovat ylinumeroituvia.
| m |
| n |
| m |
| 1 |
| 5 |
| 1 |
| m |
| n |
| 2m |
| 2n |
| 3m |
| 3n |
Jokainen numeroituva reaalilukujen osajoukko on nollamitallinen
Käytimme vertailua < eikä ≤, koska jatkon kannalta kumpikin kelpaisi ja jotain piti valita. Valinta < johtaa hitusen dramaattisempaan lopputulokseen kuin ≤, koska sen mukaan tikku peittää hiukan vähemmän lukuja: tikun päätepisteet eivät peitä mitään.
| 1 |
| 2 |
| 2 |
| 1 |
| 1 |
| 1 |
| m |
| n |
| m |
| n |
| 2m |
| 2n |
| 3m |
| 3n |
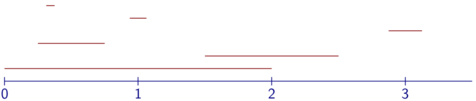
Olemme siis peittäneet jokaisen positiivisen rationaaliluvun, vieläpä äärettömän moneen kertaan, yhdestä tikusta leikatuilla pätkillä. Tikun pituus p on mielivaltainen positiivinen reaaliluku. Se voi olla 1, 0.1 tai vaikka 0.0000000001.
Lukusuoran nollasta oikealle menevä puolisuora on äärettömän pituinen. Näyttää ikään kuin olisimme peittäneet sen äärellisen pituisesta janasta leikatuilla pätkillä. Itse asiassa jana saa olla miten lyhyt tahansa paitsi nollan pituinen (eli sen pituus p saa olla miten pieni positiivinen reaaliluku tahansa). Tämä tuntuu järjenvastaiselta.
Tämän ongelman ratkaisu koostuu kolmesta osasta.
Ensiksi, on hyvä huomata heti alkuun, että ongelma ei koske todellista fysikaalista maailmaamme vaan matemaattisten abstraktioiden maailmaa. Todellista tikkua ei voi puolittaa miten monta kertaa tahansa. Todellinen tikku ei voi olla lyhyempi kuin esimerkiksi atomi.
| q |
| 2 |
Peitimme edellä tikunpätkillä kaikki positiiviset rationaaliluvut, mutta sama päättely toimii jokaiselle numeroituvalle lukujoukolle. Siksi jokainen numeroituva lukujoukko on nollamitallinen.
Kolmanneksi, niin omituiselta kuin se tuntuukin, mielivaltaisen pituinen tikku (paitsi nollan pituinen) todella riittää peittämään suoran pisteitä siten, että vaikka jokaista pistettä ei peitetäkään, jokaisen pisteen lähellä on peitetty piste. Hyvin lähellä. Valitsetpa minkä tahansa reaaliluvun x ja minkä tahansa positiivisen reaaliluvun r, lukujen x − r ja x + r välillä on äärettömän monta rationaalilukua. Esimerkiksi luku y, joka saadaan katkaisemalla x:n desimaaliesitys k desimaalin jälkeen, on rationaaliluku joka poikkeaa x:stä enintään 10−k:n verran. Valitsemalla tarpeeksi suuri k saadaan x − r < y < x + r. Siihen riittää k ≥ ⌊1 − log r⌋.
Ihmiskunnalla on ollut vaikeuksia löytää, miten tämä asiakokonaisuus menee ja hyväksyä, että niin se menee. Se, että on muitakin lukuja kuin rationaaliluvut, keksittiin antiikin aikana. Legenda kertoo, että keksintö järkytti aikalaisia niin pahasti, että he tappoivat keksijän nimeltä Hippasus. Ylinumeroituvuuden keksijä Georg Cantor (1845–1918) kohtasi paljon jyrkkää vastustusta muilta matemaatikoilta. Elämänsä viimeiset yli 30 vuotta Cantor kärsi toistuvasta masennuksesta. Nykyisin Cantorin katsotaan olleen oikeassa ja hänen vastustajiensa väärässä, ja Cantorin tuloksia pidetään erittäin merkittävinä.
Nykyisinkin netin keskustelupalstoilta löytyy sinnikkäitä keskustelijoita (tai ehkä ei oikeastaan keskustelijoita vaan vänkääjiä), jotka väittävät kumonneensa ylinumeroituvuuden olemassaolon. Kaksi muuta tulosta, joita vastaan hyökätään netissä raivoisasti, ovat Gödelin epätäydellisyyslauseet, joka on modernin logiikan mahdollisesti tärkein saavutus; sekä pysähtymistesterin olemattomuus, joka on keskeinen teoreettisessa tietojenkäsittelytieteessä. Kahden viimeksi mainitun välillä on läheinen yhteys, eivätkä ne ole ylinumeroituvuudesta tolkuttoman kaukana.
Tällä alalla saavutetuissa tuloksissa ei ole sisäisiä ristiriitaisuuksia, moni tulos viittaa samaan suuntaan, ja lähes kaikki asiantuntijat hyväksyvät ne. Siltä varalta, että olet se nero, joka huomaa mikä siinä kaikessa on vikana ja keksii paremman teorian, haluan antaa yhden neuvon. Ennen kuin alat julistaa uutta oppiasi maailmalle, pidä huoli, että tiedät hyvin, hyvin tarkasti, miten nykyinen oppi menee. Muuten kukaan asiantuntija ei kuuntele sinua.
Koetpa itsesi neroksi tai et, ehkä on parempi, että et tutustu Banach-Tarskin paradoksiin ☺.
Nyt kun on jonkin aikaa jaariteltu, katsotaanpa, muistatko tärkeimmät tässä tehtävässä esitellyt käsitteet.
Tämä riittäköön tällä kertaa!