* Huom. Tämä on kesken*

Aihe

Tällä viikolla hyppäämme pois liukuhihnojen turvallisesta maailmasta ja ryhdymme tutkimaan normaalimaailmasta otettuja kuvia. Huomaamme, että ellei kuvan tausta ole tasaisen värinen, emme saa erotettua meitä kiinnostavaa kohdetta taustasta kynnystämällä. Samoin huomaamme, että ellei meitä kiinnostava kohde ole litteä tai niin symmetrinen että sen 2d-projektio on aina saman muotoinen, edellisessä tutoriaalissa käytetyt muotopiirteet eivät auta meitä lainkaan.

Kuitenkin opittuamme hallitsemaan liukuhihnamaailman meitä huvittaisi osata tehdä jotakin hyödyllistä normaalimaailmassakin. Ryhdymme siis pohtimaan, millä tavalla saisimme kuvailtua järkevällä tavalla mitä tahansa näkymiä, ja etsittyä niistä meitä kiinnostavia kohteita. Esitetyt asiat löytyvät pääosin Szeliskin luvuista 3 ja 4, jotka olisi hyvä lukea.

Todellisessa maailmassa kohteiden löytäminen muistuttaa neulan haeskelua heinäsuovasta:

Kokeillaan vanhasta tottumuksesta kynnystystä..

import WebTools
import CV.Thresholding

main = web "neula-kynnystys" "images/needle_in_haystack.png" kynnystys
   where
    kynnystys :: Image GrayScale D8 -> Image GrayScale D32
    kynnystys kuva = montage (1,3) 4 [
      unsafeImageTo32F $ thresholdOtsu ZeroAndMax kuva,
      unsafeImageTo32F $ adaptiveThreshold ByMean ZeroAndMax 5 5 kuva,
      unsafeImageTo32F $ adaptiveThreshold ByMean ZeroAndMax 5 0 kuva ]

Ei tullut oikein hyvä. Unohdetaan siis tämä ja ruvetaan miettimään muuta.

Mallin sovitus

Eräs perinteinen, yksinkertainen menetelmä on mallin sovitus ( template matching ) jossa nimensä mukaisesti sovitetaan mallikuvaa tutkittavan kuvan päälle jokaiseen kohtaan, ja katsotaan mihin se sopii parhaiten. Kokeillaan!

Tässä on sopiva mallikuva:

import System.IO.Unsafe
import WebTools
import CV.TemplateMatching
import CV.ColourUtils

neula :: Image GrayScale D32
neula = unsafePerformIO $ readFromFile "images/needle.png"

main = web "neula-sovitus" "images/needle_in_haystack.png" sovitus
   where
    sovitus :: Image GrayScale D32 -> Image GrayScale D32
    sovitus kuva = montage (1,2) 4 
      [ kuva
      , stretchHistogram $ matchTemplate CCOEFF_NORMED kuva neula
      ]

Näyttää suhteellisen lupaavalta. Menetelmä siis muodostaa tuloskuvan, jonka mitat ovat alkuperäisen kuvan mitat vähennettynä mallikuvan mitoilla. Tuloskuvaan tulee vaaleita alueita sinne, missä löytyy parhaat vastaavuudet mallikuvan kanssa. Yllä olevan kuvan perusteella voitaisiin paikallistaa neula melko hyvin ainakin pystysuunnassa. Mutta entä seuraava kuva?

Parasta luovutaa. Mallin sovitus toimii hyvin vain silloin, kun etsittävä kuva on melko lailla samassa asennossa ja saman kokoinen. Tässä tilanteessa se ei auta, mutta esimerkiksi vakiokokoisia ihmiskasvoja sillä löydetään melko hyvin käyttämällä sopivaa mallikuvaa, joka on muodostettu useiden eri kasvojen keskiarvona. Sitä voi käyttää myös vertaamaan pieniä kuva-alueita esimerkiksi kulmapisteiden ympärillä.

Mainostetaan sen verran seuraavaa tutoriaalia, että varsinkin alkuperäisestä värikuvasta neula saadaan helposti esille väripiirteisiin perustuvan segmentoinnin avulla. Teeskennellään kuitenkin vielä, että meillä on vain harmaasävykuva käytössämme. Myös tässä tutoriaalissa opittavia reuna- ja suuntapiirteitä voi hyödyntää seuraavassa tutoriaalissa opittavien menetelmien kanssa.

Reunanhaku

Kynnystys ei yleensä toimi mielivaltaisissa näkymissä sen takia, että tausta ei ole tasaisen värinen, ja useimmiten tausta ei myöskään ole aina samanlainen joka kuvassa. Seuraava ajatus kohteen irrottamiseksi taustasta onkin etsiä kohteen reunat. Kiinnostaisi myös kokeilla muodostaa reunapiirre edellisessä tutoriaalissa esiteltyjen fourier-piirteiden avulla.

Reunoja esiintyy siellä, missä kuvassa tapahtuu nopeita muutoksia. Kokeillaan siis aluksi konvoluutiota maskilla, joka antaa voimakkaan vasteen sellaisissa kohdissa, joiden ympärillä tapahtuu nopeita muutoksia. Eräs yksinkertainen vaihtoehto on keskeisdifferenssi, joka käytännössä laskee pikselin molemmin puolin olevien arvojen erotuksen. Alla on tästä esimerkki.

Edistyneempiä operaattoreita ovat esimerkiksi Prewittin ja Sobelin operaattorit. Sobelin x-suuntainen maskihan on tällainen:

\(s_x = \left[\begin{array}{ccc} 1& 0& -1\\ 2& 0& -2\\ 1& 0& -1\end{array}\right]\).

import WebTools
import CV.Filters
import CV.ImageMath as IM
import CV.Matrix as M
import CV.ColourUtils

main = web "gradientit" "images/HaystackSmall.png" operaatio
   where
    operaatio :: Image GrayScale D32 -> Image GrayScale D32
    operaatio kuva = montage (3,1) 4 
      [ kuva
      , stretchHistogram $ convolve2D maskix keskipiste kuva
      , stretchHistogram $ convolve2D maskiy keskipiste kuva
      ]
    keskipiste :: (Int,Int)
    keskipiste = (1,1)
    maskix = M.fromList (3,3) [ 0,  0,  0
                              , 1,  0, -1
                              , 0,  0,  0 ]
    maskiy = M.fromList (3,3) [ 0,  1,  0 
                              , 0,  0,  0
                              , 0, -1,  0 ]

Nämä ovat eräänlaisia kuvan osittaisderivaattoja approksimoivia operaattoreita, ja yhdistämällä x- ja y-suuntainen osittaisderivaatta saadaan muodostettua kuvan gradientti, joka on normaali kaksiulotteinen vektorikenttä. Sen avulla saadaan arvioitua muutosten voimakkuutta ja suuntaa.

\(\nabla I(x,y) = (\frac{\partial I(x,y)}{\partial x}, \frac{\partial I(x,y)}{\partial y}) = (g_x,g_y)\).

Gradientin voimakkuus pisteessa \((x,y)\) on siis

\(||(g_x,g_y)|| = \sqrt{g_x^2 + g_y^2}\)

ja sen suunta on

\(\theta = arctan (\frac{g_y}{g_x})\).

OpenCV:ssä ja CV-kirjastossa suunta saadaan laskettua atan2-funktiolla (\(atan2 g_y g_x\)).

Kuvien derivaattaoperaatiot ovat herkkiä kohinalle. Hienostuneempi ja paremmin kohinaa sietävä tapa laskea osittaisderivaattoja on käyttää Gaussin funktion derivaattoja, jolloin saadaan yhdistettyä silotus ja reunanhaku. Muistamme, että kaksiulotteinen, symmetrinen Gaussin funktio on muotoa

\(G(x,y,\sigma) = \frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}\)

jolloin x-suuntainen osittaisderivaatta on

\(\frac{\partial G(x,y,\sigma)}{\partial x} = -\frac{x}{2\pi\sigma^4}e^{-\frac{x^2+y^2}{2\sigma^2}}\)

ja y-suuntainen osittaisderivaatta on

\(\frac{\partial G(x,y,\sigma)}{\partial y} = -\frac{y}{2\pi\sigma^4}e^{-\frac{x^2+y^2}{2\sigma^2}}\)

Yllä olevassa kuvassa on esitetty Gaussin funktion osittaisderivaatat kuvan muodossa. Ylärivissä nollannen ja ensimmäisen asteen derivaatat ja alarivissä toisen asteen derivaatat.

Näistä voidaan muodostaa konvoluutioydin sämpläämällä funktioiden arvoja matriisiin. Alla on koodi joka tekee tämän. Esimerkiksi jos \(\sigma = 1\) ytimen säteellä \(2\) (joka tuottaa 5x5-matriisin) x-suuntainen maski olisi tällainen (vaikka on syytä muistaa, että gaussisten ydinten säteen olisi hyvä olla \(3\sigma\) kuten varsinaisessa konvoluutiossa alla onkin; jos halutaan saada funktio mahtumaan 5x5-maskiin, voidaan käyttää \(\sigma\):aa 0.8.):

\(\left[\begin{array}{ccccc} 0.006& 0.013& 0.000& -0.013& -0.006\\ 0.026& 0.059& 0.000& -0.059& -0.026\\ 0.043& 0.097& 0.000& -0.097& -0.043\\ 0.026& 0.059& 0.000& -0.059& -0.026\\ 0.006& 0.013& 0.000& -0.013& -0.006\end{array}\right]\)

import WebTools
import CV.Filters
import CV.ImageMath as IM
import CV.Matrix as M
import CV.ColourUtils

g :: Float -> (Int,Int) -> Float
g s (x,y) = (1 / (2 * pi * s**2)) * exp(-((ix**2 + iy**2) / (2 * s**2)))
  where
    ix = fromIntegral x
    iy = fromIntegral y

gx :: Float -> (Int,Int) -> Float
gx s (x,y) = (-(ix / (2 * pi * s**4))) * exp(-((ix**2 + iy**2) / (2 * s**2)))
  where
    ix = fromIntegral x
    iy = fromIntegral y

gy :: Float -> (Int,Int) -> Float
gy s (x,y) = (-(iy / (2 * pi * s**4))) * exp(-((ix**2 + iy**2) / (2 * s**2)))
  where
    ix = fromIntegral x
    iy = fromIntegral y

kernel :: ((Int,Int) -> Float) -> Int -> [Float]
kernel f r = [f (x,y) | y <- [-r..r] , x <- [-r..r] ]

main = web "gaussian-derivaatat" "images/HaystackSmall.png" operaatio
   where
    operaatio :: Image GrayScale D32 -> Image GrayScale D32
    operaatio kuva = montage (3,1) 4 
      [ gaussian (7,7) $ kuva
      , stretchHistogram $ convolve2D maskix keskipiste kuva
      , stretchHistogram $ convolve2D maskiy keskipiste kuva
      ]
    keskipiste :: (Int,Int)
    keskipiste = (3,3)
    maskix = M.fromList (7,7) $ kernel (gx 1.0) 3
    maskiy = M.fromList (7,7) $ kernel (gy 1.0) 3

On myös hyvä muistaa, että x- ja y-suuntainen \(\sigma\) voi olla erilainen, jolloin saadaan pitkänomaisen ellipsin muotoisia maskeja. Tehokasta toteutusta tarvittaessa on myös syytä muistaa, että Gaussin funktio on separoituva: 2-ulotteinen konvoluutio saadaan tehtyä nopeammin tekemällä peräkkäin kaksi 1-ulotteista konvoluutiota.

Gaussin derivaattojen avulla saadaan myös helposti määriteltyä ns. ohjattavia filttereitä ( steerable filters ) joilla voidaan etsiä kuvasta ns. suunnattua energiaa ( oriented energy ) eli vahvoja muutoksia tarkoin rajattuun suuntaan. Näitä voidaan käyttää reunojen lisäksi myös tekstuurien analysointiin. Ohjattava filtteri saadaan yksinkertaisesti kertomalla gradienttikenttää halutun suuntaisella yksikkövektorilla. Jos \(\hat{u}\) on yksikkövektori kulmassa \(\theta\)

\(\hat{u} = (u_x,u_y) = (cos\theta, sin\theta)\)

ja \(g_x\) ja \(g_y\) ovat osittaisderivaatat, niin suuntaan \(\theta\) kierretyn suunnatun filtterin antama tulos on

\(g_{\theta} = u_x g_x + u_y g_y\).

Koodi joka tekee tämän on esitetty alla.

import WebTools
import CV.Filters
import CV.ImageMath as IM
import CV.ImageMathOp
import CV.Matrix as M
import CV.ColourUtils

gx :: Float -> (Int,Int) -> Float
gx s (x,y) = (-(ix / (2 * pi * s**4))) * exp(-((ix**2 + iy**2) / (2 * s**2)))
  where
    ix = fromIntegral x
    iy = fromIntegral y

gy :: Float -> (Int,Int) -> Float
gy s (x,y) = (-(iy / (2 * pi * s**4))) * exp(-((ix**2 + iy**2) / (2 * s**2)))
  where
    ix = fromIntegral x
    iy = fromIntegral y

kernel :: ((Int,Int) -> Float) -> Int -> [Float]
kernel f r = [f (x,y) | y <- [-r..r] , x <- [-r..r] ]

steerable theta i = (ux |* igx) #+ (uy |* igy)
  where
    (ux,uy) = (cos theta, sin theta)
    c :: (Int,Int)
    c = (3,3)
    igx = (convolve2D (M.fromList (7,7) $ kernel (gx 1.0) 3) c i)
    igy = (convolve2D (M.fromList (7,7) $ kernel (gy 1.0) 3) c i)

main = web "suunnatut-filtterit" "images/HaystackSmall.png" operaatio
   where
    operaatio :: Image GrayScale D32 -> Image GrayScale D32
    operaatio kuva = montage (3,1) 4 
      [ stretchHistogram $ steerable (3*pi/4) kuva
      , stretchHistogram $ steerable (-5*pi/8) kuva
      , stretchHistogram $ steerable (pi/4) kuva
      ]

Kaikkia näitä menetelmiä käytettäessa törmätään kuitenkin kysymykseen: mitä teemme näille filtteröinnin tuloksena saataville kuville, joissa on vahva vaste tietyn suuntaisille reunoille? On syytä huomata, että ensimmäisen asteen derivaatat tuottavat sekä positiivisia että negatiivisia arvoja, ja reunakohdat löytyvät derivaattojen ääriarvoista. Yksi mahdollisuus on tietysti laskea gradienttikentän magnitudi (tai ottaa itseisarvo jos käytetään vain yhdensuuntaista osittaisderivaattaa) ja tuttuun tapaan kynnystää tuloksena oleva reunakuva (alarivissä on esitetty gradientin magnitudi ja suunta):

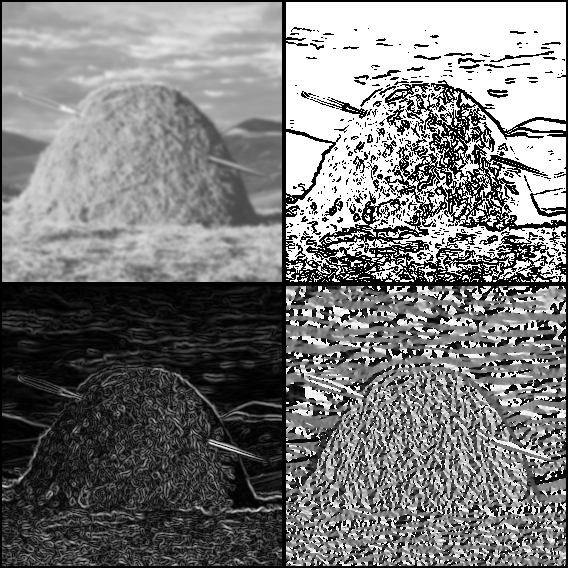
import WebTools
import CV.Filters
import CV.ImageMath as IM
import CV.ImageMathOp
import CV.Matrix as M
import CV.ColourUtils
import CV.Thresholding

g :: Float -> (Int,Int) -> Float
g s (x,y) = (1 / (2 * pi * s**2)) * exp(-((ix**2 + iy**2) / (2 * s**2)))
  where
    ix = fromIntegral x
    iy = fromIntegral y

gx :: Float -> (Int,Int) -> Float
gx s (x,y) = (-(ix / (2 * pi * s**4))) * exp(-((ix**2 + iy**2) / (2 * s**2)))
  where
    ix = fromIntegral x
    iy = fromIntegral y

gy :: Float -> (Int,Int) -> Float
gy s (x,y) = (-(iy / (2 * pi * s**4))) * exp(-((ix**2 + iy**2) / (2 * s**2)))
  where
    ix = fromIntegral x
    iy = fromIntegral y

kernel :: ((Int,Int) -> Float) -> Int -> [Float]
kernel f r = [f (x,y) | y <- [-r..r] , x <- [-r..r] ]

main = web "gradientti-kynnystetty" "images/HaystackSmall.png" operaatio
   where
    operaatio :: Image GrayScale D32 -> Image GrayScale D32
    operaatio kuva = montage (2,2) 4 
      [ gaussian (7,7) $ kuva
      , thresh
      , stretchHistogram $ imag
      , stretchHistogram $ iang
      ]
      where
        keskipiste :: (Int,Int)
        keskipiste = (3,3)
        maskix = M.fromList (7,7) $ kernel (gx 1.0) 3
        maskiy = M.fromList (7,7) $ kernel (gy 1.0) 3
        igx = convolve2D maskix keskipiste kuva
        igy = convolve2D maskiy keskipiste kuva
        imag = IM.sqrt $ (igx #* igx) #+ (igy #* igy)
        iang = IM.atan2 igy igx
        thresh = unsafeImageTo32F $ thresholdOtsu ZeroAndMax $ unsafeImageTo8Bit $ stretchHistogram imag

Näillä luultavasti saisi tehtyä jotakin, jos vielä ohentaa paksut reunat morfologian avulla ja jollakin lailla karsii ylimääräiset reunat.

Cannyn menetelmä

Eräs vaihtoehto objektien tunnistamiselle on etsiä reunakäyriä yhdistämällä löydettyjä reunapisteitä pitemmäksi ketjuksi. Tunnetuin menetelmä tämän tekemiseksi on Cannyn reunanhaku. Tämän menetelmän vaiheet ovat

• kuvan silotus gaussisella suotimella,
• gradienttikentän muodostaminen joillakin osittaisderivaattaoperaattoreilla,
• gradientin magnitudin laskeminen,
• gradientin suunnan pyöristys neljään pääsuuntaan (vaakasuora, pystysuora ja kaksi diagonaalia),
• kuvasta etsitään gradientin lokaalit maksimit huomioiden pikselin naapurit jotka ovat suorassa kulmassa gradientin suuntaa vastaan (eli jos suunta on vaakasuoraan, tutkitaan ylä- ja alapuolella olevia naapureita),
• reunojen seuranta kynnystämällä hystereesin avulla, eli kynnystämällä ensin suurempaa kynnysarvoa käyttäen esille melko varmat reunat, ja lisäämällä näihin naapureita jotka ovat pienempää kynnysarvoa suurempia.

Tätä menetelmää pidetään jossakin määrin optimaalisena keinona löytää kuvasta hyviä reunoja. Hieman tarkempi ja matemaattisesti vahvempi tapa on differentiaaligeometriaan perustuva reunanhaku, jossa hyödynnetään korkeampia osittaisderivaattoja skaala-avaruudessa, mutta siihen emme mene tässä yhteydessä.

OpenCV:ssä on Cannyn menetelmän toteutus. Tätä voi käyttää alustavien reunakäyrien etsimiseen, mutta kokeilu osoittanee että useimmiten näin saadut reunat ovat käyttökelpoisia lähinnä syötteenä jatkokäsittelylle, jossa voidaan sovittaa reunojen sisälle esimerkiksi polygoneja tai muita muotoja.

import WebTools
import CV.Filters
import CV.Edges
import CV.ColourUtils

main = web "canny-reunat" "images/HaystackSmall.png" operaatio
   where
    operaatio :: Image GrayScale D32 -> Image GrayScale D32
    operaatio kuva = montage (2,1) 4 
      [ gaussian (7,7) $ kuva
      , unsafeImageTo32F reunat
      ]
      where
        reunat = canny 192 128 7 $ unsafeImageTo8Bit kuva

Menetelmä löytää tosiaan hyviä, ehjiä reunakäyriä, mutta ongelmaksi muodostuu turhien reunojen karsiminen.

Toisen asteen derivaatat

Edellä käsiteltiin kuvan ensimmäisen asteen osittaisderivaattoja ja gradienttia. Näiden kanssa tulee ongelmaksi löytää derivaattojen ääriarvot. Koska on helpompaa löytää toisen asteen derivaatan nollakohta kuin ensimmäisen asteen derivaatan ääriarvo, usein on tapana käyttää reunanhakuun toisen asteen osittaisderivaattoja. Erittäin yleinen menetelmä on käyttää Laplacen operaattoria jossa lasketaan yhteen kuvan x- ja y-suuntaiset toisen asteen osittaisderivaatat:

\(L(x,y) = \frac{\partial^2 I(x,y)}{\partial x^2} + \frac{\partial^2 I(x,y)}{\partial y^2}\).

Tätä operaattoria ja myös toisen asteen derivaattoja voidaan approksimoida konvoluutiomaskeilla, esimerkiksi

\(l = \left[\begin{array}{ccc} 0& 1& 0\\ 1& -4& 1\\ 0& 1& 0\end{array}\right]\).

Koska toisen asteen derivaatat reagoivat kohinaan vielä voimakkaammin kuin ensimmäisen asteen derivaatat, niiden kanssa on yleensä syytä käyttää silotusta kohinan vähentämiseksi. Gaussin funktion derivaatat ovatkin erityisen hyödyllisiä tässä:

\(\begin{align*} \frac{\partial^2 G(x,y,\sigma)}{\partial x^2} & = \frac{(-1 + \frac{x^2}{\sigma^2})}{2\pi\sigma^4}e^{-\frac{x^2 + y^2} {2\sigma^2}}\\ \frac{\partial^2 G(x,y,\sigma)}{\partial y^2} & = \frac{(-1 + \frac{y^2}{\sigma^2})}{2\pi\sigma^4}e^{-\frac{x^2 + y^2}{2\sigma^2}}\\ \frac{\partial^2 G(x,y,\sigma)}{\partial x \partial y} & = \frac{xy}{2\pi\sigma^6}e^{-\frac{x^2 + y^2}{2\sigma^2}} \end{align*}\)

Mistä tahansa Gaussin funktion osittaisderivaattojen asteesta saadaan tehtyä ohjattava filtteri. Toisen asteen derivaatoista se saadaan tehtyä näin:

\(g^2_\theta = u_x^2 g^2_{xx} + 2 u_x u_y g^2_{xy} + u_y^2 g^2_{yy}\)

import WebTools
import CV.Filters
import CV.ImageMath as IM
import CV.ImageMathOp
import CV.Matrix as M
import CV.ColourUtils

g2x2 :: Float -> (Int,Int) -> Float
g2x2 s (x,y) = (-1 + ix**2/s**2) / (2 * pi * s**4) * (exp (-((ix**2 + iy**2) / (2 * s**2))))
  where
    ix = fromIntegral x
    iy = fromIntegral y

g2y2 :: Float -> (Int,Int) -> Float
g2y2 s (x,y) = (-1 + iy**2/s**2) / (2 * pi * s**4) * (exp (-((ix**2 + iy**2) / (2 * s**2))))
  where
    ix = fromIntegral x
    iy = fromIntegral y

g2xy :: Float -> (Int,Int) -> Float
g2xy s (x,y) = (ix * iy) / (2 * pi * s**6) * (exp (-((ix**2 + iy**2) / (2 * s**2))))
  where
    ix = fromIntegral x
    iy = fromIntegral y

steerable2 theta i = ((ux**2) |* ig2x2) #+ ((2*ux*uy) |* ig2xy) #+ ((uy**2) |* ig2y2)
  where
    (ux,uy) = (cos theta, sin theta)
    c :: (Int,Int)
    c = (2,2)
    ig2x2 = (convolve2D (M.fromList (7,7) $ kernel (g2x2 1.0) 3) c i)
    ig2y2 = (convolve2D (M.fromList (7,7) $ kernel (g2y2 1.0) 3) c i)
    ig2xy = (convolve2D (M.fromList (7,7) $ kernel (g2xy 1.0) 3) c i)

kernel :: ((Int,Int) -> Float) -> Int -> [Float]
kernel f r = [f (x,y) | y <- [-r..r] , x <- [-r..r] ]

main = web "toisen-asteen-derivaatat" "images/HaystackSmall.png" operaatio
   where
    operaatio :: Image GrayScale D32 -> Image GrayScale D32
    operaatio kuva = montage (2,3) 4 
      [ gaussian (7,7) kuva
      , stretchHistogram $ ilog
      , stretchHistogram $ ig2x2
      , stretchHistogram $ ig2y2
      , stretchHistogram $ ig2xy
      , stretchHistogram $ isteerable2
      ]
      where
        keskipiste :: (Int,Int)
        keskipiste = (3,3)
        maskix2 = M.fromList (7,7) $ kernel (g2x2 1.0) 3
        maskiy2 = M.fromList (7,7) $ kernel (g2y2 1.0) 3
        maskixy = M.fromList (7,7) $ kernel (g2xy 1.0) 3
        ig2x2 = convolve2D maskix2 keskipiste kuva
        ig2y2 = convolve2D maskiy2 keskipiste kuva
        ig2xy = convolve2D maskixy keskipiste kuva
        ilog = ig2x2 #+ ig2y2
        isteerable2 = steerable2 (pi/4) kuva

Yllä olevan kuvamatriisin ylärivissä oikealla on kuva, jossa on tulos operaatiosta \(g^2_{xx} + g^2_{yy}\). Tämä on siis Laplacen operaatio, joka on tehty Gaussin funktiolle. Kyseessä on hyvin tunnettu operaattori nimeltä Laplacian of Gaussian (LoG) ja se antaa voimakkaita vasteita sellaisille kohdille, joissa on tumman keskustan ympärillä vaaleampaa tai vaalean keskustan ympärillä tummempaa. Muuttamalla Gaussin funktion \(\sigma\):aa saadaan säädettyä, minkä kokoisille kohteille operaattori on herkkä. Neurotieteen tutkijat ovat osoittaneet, että silmän verkkokalvoilla on neuroneita (gangliasoluja) jotka antavat samantapaisia center-surround-vasteita eri skaaloissa. Evoluutio on siis osoittanut tämän tapaisen operaattorin hyödyllisyyden.

LoG-operaattoria voidaan approksimoida laskemalla kahden eri kokoisen Gaussin ytimen erotus, eli konvolvoimalla kuva kahdella eri kokoisella gaussisella maskilla ja laskemalla tulosten erotus. Tämän operaattorin nimi on Difference of Gaussians (DoG) ja se on lähellä LoG:tä kun kahden ytimen koon suhde on noin 1.6, eli esimerkiksi 3 ja 5 tai 7 ja 11. Vielä karkeampi approksimaatio saadaan käyttämällä ns. difference of boxes -operaattoria, jossa lasketaan kahden eri kokoisen laatikkofiltterin (keskiarvosuotimen) erotus. Tämä on erityisen hyödyllinen käytettäessä integraalikuvia, sillä niiden avulla saadaan laskettua minkä tahansa nelikulmaisen alueen summa kolmella laskutoimituksella. Näitä operaattoreita käytetään monissa tunnetuissa pistepiirteiden etsintämenetelmissä, joista lisää jäljempänä.

Houghin muunnos

Joissakin tilanteissa kuvista halutaan löytää suoria linjoja tai muita geometrisia muotoja, kuten ympyröitä tai ellipsejä. Perinteinen ja toimiva menetelmä on Houghin muunnos, jossa muodostetaan etsittäville muodoille parametriavaruus, ja jokainen reunapiste äänestää mahdollisia kyseisen pisteen kautta kulkevan suoran, ellipsin tms. parametreja. Tästä muodostuu siis eräänlainen parametriavaruuden histogrammi, jonka maksimiarvot kertovat, millä parametreilla muoto saadaan sovitettua kuvaan.

Käsitellään tätä enemmän maanantaina jos ehditään..

Pistepiirteet

Kohteiden reunoja haeskellessamme huomaamme, että kohteiden kuvailu reunakäyrän perusteella on hankalaa. Muotopiirteet soveltuvat kuvailemaan lähinnä kohteita, joiden koko reunakäyrä on tiedossa. On kuitenkin melkoisen vaikeaa saada kuvasta irti yhtenäinen reuna tietylle kohteelle. Reunoja löytyy aivan liikaa, ne muodostavat harvoin ehjän kohteen ympäri menevän ketjun, ja joka tapauksessa hyödyllinen reunakäyrä saadaan vain tasaisen värisille kohteille. Lisäksi kohteen pitäisi näyttää saman muotoiselta joka suunnasta.

Seuraava idea on kuvailla kohdetta kokoelmana irrallisia palasia. Ideana on se, että vaikka koko kohde ei olisikaan kunnolla näkyvissä, ja vaikka kohde olisi eri asennossa kuin edellisellä kerralla, jos kuvasta löydetään riittävän monta samanlaista kohteen palasta, kohde on luultavasti löytynyt.

Nurkkien haku

Kuvasta on helpointa paikallistaa sellaisia kohtia, joissa kaksi reunaa muodostaa selkeän nurkan. Tämmöiset sijaitsevat luultavimmin ympäristöissä, joissa on kaksi voimakasta, selvästi eri suuntiin osoittavaa gradienttia.

Helpoin keino nurkkien löytämiseen ovat erilaiset konvoluutiomaskit, esimerkiksi

\(c = \left[\begin{array}{ccc} 1& -2& 1\\ -2& 4& -2\\ 1& -2& 1\end{array}\right]\).

Harrisin menetelmä

Perinteinen, suosittu, toimiva ja intuiviinen tapa etsiä sopivia kohtia pistepiirteiden irrotusta varten on Harrisin menetelmä. Tämä perustuu siihen ajatukseen, että kuvasta kannattaa etsiä sellaisia pisteitä, jotka on mahdollisimman helppo paikallistaa esimerkiksi eri suunnasta otetusta kuvasta. Tällaisia ovat esimerkiksi kohdat, joissa on voimakkaita kaaria tai nurkkia tai muita ympäristöstä erottuvia yksityiskohtia.

Sitä, kuinka hyvin piste erottuu ympäristöstään, saadaan tietysti arvioitua vertaamalla pisteen ympäristöä muihin lähistöllä oleviin ympäristöihin laskemalla esimerkiksi painotettuja neliöllisten etäisyyksien summia ympäristön ja siirrettyjen ympäristöjen välillä. Tämä tietysti vaatii paljon laskemista. Keskeinen ajatus Harrisin menetelmässä onkin arvioida tätä pisteympäristön autokorrelaatiota rakennetensorin (structure tensor) eli gradienteista muodostetun matriisin avulla. Rakennetensori kuvaa pisteympäristön pääasiallisia muutossuuntia. Matriisia kutsutaan joskus myös toiseksi momenttimatriisiksi.

\(A = w ** \left[\begin{array}{cc} g_x^2& g_x g_y\\ g_y g_x& g_y^2\end{array}\right]\)

missä \(w\) on painotettu keskiarvomaski. Käyttämällä esimerkiksi gaussista maskia saadaan tuloksesta isotrooppinen eli suunnasta riippumaton. Tämä matriisi sisältää siis painotetut keskiarvot tietyn pisteen ympäristössä esiintyvistä gradienteista. Laskemalla tämän matriisin ominaisarvot voidaan analysoida ympäristön muotoa.

• Jos molemmat ominaisarvot ovat pieniä, ympäristö on tasainen.
• Jos toinen ominaisarvo on pieni ja toinen suuri, piste on reunalla jossa on yksi voimakas gradientti.
• Jos molemmat ominaisarvot ovat suuria, piste on kulmassa jossa on kaksi voimakasta gradienttia.

Tunnettu Shi-Tomasi-menetelmä käyttää kulmapisteen hyvyysarvona tämän matriisin pienintä ominaisarvoa, ja kirjallisuuden mukaan tämä lisää erityisesti kulmapisteiden vakautta kun pyritään seuraamaan pisteitä kuvaruudusta toiseen. Pienen matriisin ominaisarvotkin saadaan laskettua melko helposti, mutta Harrisin mukaan tämä voidaan välttää tutkimalla sen sijaan vastefunktiota

\(\begin{align*} R(A) & = \lambda_1\lambda_2 - \kappa(\lambda_1 + \lambda_2)^2\\ & = det(A) - \kappa trace^2(A)\\ & = (A_{11}A_{22} - A_{12}A_{21}) - \kappa (A_{11} + A_{22})^2\\ & = (g_x^2 g_y^2 - (g_x g_y)^2) - \kappa (g_x^2 + g_y^2)^2 \end{align*}\)

missä \(\lambda_1\) ja \(lambda_2\) ovat rakennetensorin ominaisarvot ja \(\kappa\) on vapaa parametri, jolla säädetään funktion herkkyyttä. Yleisesti käytetty arvo on 0.04, ja kirjallisuuden mukaan arvot 0.04-0.15 ovat toimivia. CV-kirjaston matemaattisten operaatioiden ja edellä opittujen gaussisten derivaattamaskien avulla on helppo laskea Harrisin vastearvot: ylärivissä vasemmalla on CV-kirjaston harris-toteutuksen tuottama tulos, oikealla on käsin laskettu tulos. Alemmilla riveillä on rakennetensorin alkioiden arvot levitettyinä kuviksi, eli sen sijaan että meillä on kuva jossa on 2x2-matriisi jokaisessa pisteessä, meillä on 2x2-matriisi kuvia. Tulos on erilainen keskialueen arvojen osalta, mutta samanlainen maksimiarvojen osalta.

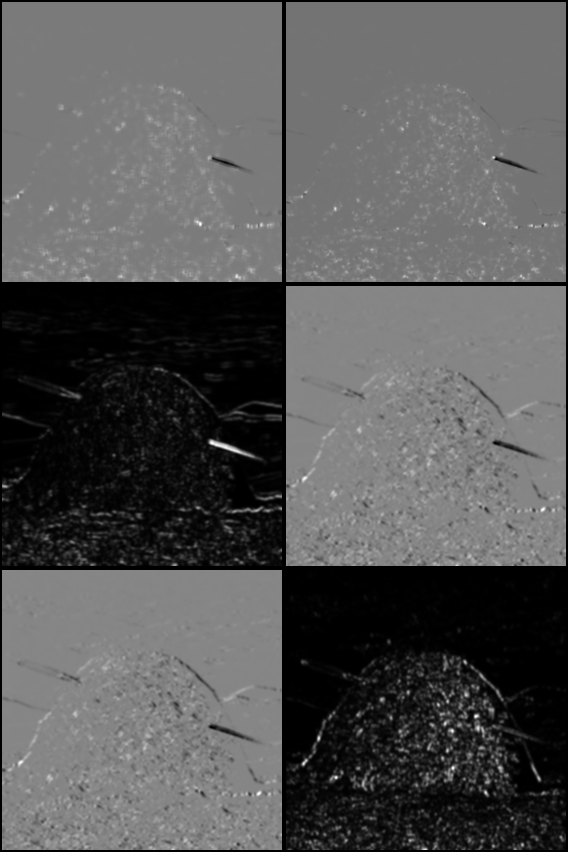
import WebTools
import CV.Filters
import CV.ImageMath as IM
import CV.ImageMathOp
import CV.Matrix as M
import CV.ColourUtils
import CV.Corners

gx :: Float -> (Int,Int) -> Float
gx s (x,y) = (-(ix / (2 * pi * s**4))) * exp(-((ix**2 + iy**2) / (2 * s**2)))
  where
    ix = fromIntegral x
    iy = fromIntegral y

gy :: Float -> (Int,Int) -> Float
gy s (x,y) = (-(iy / (2 * pi * s**4))) * exp(-((ix**2 + iy**2) / (2 * s**2)))
  where
    ix = fromIntegral x
    iy = fromIntegral y

kernel :: ((Int,Int) -> Float) -> Int -> [Float]
kernel f r = [f (x,y) | y <- [-r..r] , x <- [-r..r] ]

main = web "harrisin-vaste" "images/HaystackSmall.png" operaatio
   where
    operaatio :: Image GrayScale D32 -> Image GrayScale D32
    operaatio kuva = montage (2,3) 4 
      [ stretchHistogram $ harris 5 5 0.04 kuva
      , stretchHistogram $ r
      , stretchHistogram $ a11
      , stretchHistogram $ a12
      , stretchHistogram $ a21
      , stretchHistogram $ a22
      ]
      where
        c :: (Int,Int)
        c = (2,2)
        igx = (convolve2D (M.fromList (5,5) $ kernel (gx 0.8) 2) c kuva)
        igy = (convolve2D (M.fromList (5,5) $ kernel (gy 0.8) 2) c kuva)
        a11 = gaussian (5,5) $ igx #* igx
        a22 = gaussian (5,5) $ igy #* igy
        a12 = gaussian (5,5) $ igx #* igy
        a21 = gaussian (5,5) $ igy #* igx
        kappa = 0.04
        r = ((a11 #* a22) #- (a12 #* a21)) #- (kappa |* ((a11 #+ a22) #* (a11 #+ a22)))

On syytä huomata, että tämä menetelmä laskee vain tietynlaisen vastefunktion arvon. Se antaa suuria arvoja hyvin ympäristöstään erottuville pisteille, ja usein suuria arvoja on useita lähekkäin. Ennen löydettyjen pisteiden hyödyntämistä on yleensä tehtävä ns. non-maximal suppression eli valittava tietystä ympäristöstä vain lokaalit maksimiarvot. Samoin löydettyjä kulmapisteitä kannattaa kynnystää esimerkiksi ottamalla mukaan vain ne, joiden vaste on vaikkapa 0.1 kertaa suurimman vasteen arvo. Esimerkkikoodi (vaikka ei kovin tehokas) tämän tekemiseen on kansiossa ilman_graphicstoolsia/Harris.hs. Tätä koodia voi käyttää pohjana tutoriaalitehtävän ratkaisussa.

Lisätietoa Harrisin menetelmästä ja kulmanhausta wikipediassa. Menetelmä on edelleen suosittu, koska se löytää melko intuitiivisia kulmapisteitä, ja löydetyt pisteet ovat yleensä erilaisia kuin modernien menetelmien löytämät. Sitä voidaan siis käyttää yhdessä esimerkiksi SIFT- tai SURF-menetelmien kanssa.

Skaala-avaruus

Harrisin menetelmä löytää pisteitä, jotka sietävät suhteellisen hyvin valaistuksen muutoksia, siirtoja ja ja kiertoja. Se kuitenkin löytää pisteitä vain yhdessä skaalassa: jos kohdetta skaalataan merkittävästi, löydetyt pisteet eivät enää ole samanlaisia. Tähän ongelmaan on ratkaisuna kuvapyramidi, jossa muodostetaan useita skaalattuja versioita samasta kuvasta, ja etsitään pisteitä jokaisessa skaalassa erikseen.

Harrisin menetelmän pohjalta on kehitetty ns. Harrisin affiini, jonka löytämät pisteet sietävät hyvin affiineja muunnoksia, eli kuvakulman ja skaalan muutoksia, kiertoja, siirtoja, ja vääntöjä. Se muodostetaan laskemalla edellä kuvattuja rakennetensoreita käyttäen useita eri \(\sigma\):n arvoja. Kukin löydetty piste lokalisoidaan skaalassa etsimällä se skaala, jossa Laplacian-of-Gaussian (LoG) maksimoituu.

Toinen suosittu skaala-invariantti menetelmä on Hessen affiini, joka on lähes identtinen Harrisin affiinin kanssa mutta jossa käytetään Hessen matriisia rakennetensorin sijaan. Hessen matriisi sisältää kuvan toisen asteen osittaisderivaatat:

\(H = \left[\begin{array}{cc} g^2_{xx}& g^2_{xy}\\ g^2_{xy}& g^2_{yy}\end{array}\right]\)

missä

\(\begin{align*} g^2_{xx} & = \frac{\partial^2 I(x,y)}{\partial x^2}\\ g^2_{yy} & = \frac{\partial^2 I(x,y)}{\partial y^2}\\ g^2_{xy} & = \frac{\partial^2 I(x,y)}{\partial x \partial y}\\ \end{align*}\).

Hessen matriisi kuvaa kuvafunktion kaarevuutta kyseisessä pisteessä. Matriisin determinantti antaa vahvoja vasteita pisteissä, joissa on vahva gradientti kahteen eri suuntaan. Determinant of Hessian (DoH) onkin eräs suosittu keino löytää pistemäisiä kohteita kuvasta. Hessen affiini sen sijaan etsii pisteitä, joissa sekä determinantti että jälki ( trace ) saa lokaalin maksimiarvon. Huomaamme, että \(trace(H) = g^2_{xx} + g^2_{yy}\) eli se vastaa Laplacian of Gaussian -operaattorin arvoa kuvapisteessä. Hessen affiini yhdistää siis kaksi tehokasta pistemäisten kohteiden etsintään soveltuvaa operaattoria (DoH ja LoG). Koska LoG reagoi voimakkaasti myös reunoihin, näistä saadaan DoH:n avulla karsittua esille ne reunapisteet, joissa on myös selkeä kulma tai kaarevuusmaksimi.

Alla olevassa kuvassa lasketaan DoH ja LoG ja verrataan tuloksia.

import WebTools
import CV.Filters
import CV.ImageMath as IM
import CV.ImageMathOp
import CV.Matrix as M
import CV.ColourUtils

g2x2 :: Float -> (Int,Int) -> Float
g2x2 s (x,y) = (-1 + ix**2/s**2) / (2 * pi * s**4) * (exp (-((ix**2 + iy**2) / (2 * s**2))))
  where
    ix = fromIntegral x
    iy = fromIntegral y

g2y2 :: Float -> (Int,Int) -> Float
g2y2 s (x,y) = (-1 + iy**2/s**2) / (2 * pi * s**4) * (exp (-((ix**2 + iy**2) / (2 * s**2))))
  where
    ix = fromIntegral x
    iy = fromIntegral y

g2xy :: Float -> (Int,Int) -> Float
g2xy s (x,y) = (ix * iy) / (2 * pi * s**6) * (exp (-((ix**2 + iy**2) / (2 * s**2))))
  where
    ix = fromIntegral x
    iy = fromIntegral y

kernel :: ((Int,Int) -> Float) -> Int -> [Float]
kernel f r = [f (x,y) | y <- [-r..r] , x <- [-r..r] ]

main = web "hessen-affiini" "images/HaystackSmall.png" operaatio
   where
    operaatio :: Image GrayScale D32 -> Image GrayScale D32
    operaatio kuva = montage (3,1) 4 
      [ gaussian (7,7) kuva
      , stretchHistogram $ idoh
      , stretchHistogram $ ilog
      ]
      where
        keskipiste :: (Int,Int)
        keskipiste = (3,3)
        maskix2 = M.fromList (7,7) $ kernel (g2x2 1.0) 3
        maskiy2 = M.fromList (7,7) $ kernel (g2y2 1.0) 3
        maskixy = M.fromList (7,7) $ kernel (g2xy 1.0) 3
        ig2x2 = convolve2D maskix2 keskipiste kuva
        ig2y2 = convolve2D maskiy2 keskipiste kuva
        ig2xy = convolve2D maskixy keskipiste kuva
        idoh = (ig2x2 #* ig2y2) #- (ig2xy #* ig2xy)
        ilog = ig2x2 #+ ig2y2

Lisätietoa Mikolajczykin ja Schmidin Harrisin affiinista ja Hessen affiinista wikipediasta. Myös alkuperäiset paperit ovat selkeitä ja erittäin mielenkiintoisia, ja niihin kannattaa tutustua jos pistepiirteet kiinnostavat.

Pisteiden kuvailu piirteiden avulla

Tähän asti olemme etsineet kuvasta vain pisteitä. Niistä saadaan pistepiirteitä vasta sitten, kun pisteiden ympäristöä kuvaillaan jollakin matemaattisesti vertailtavalla tavalla. Perinteinen keino oli ottaa talteen esimerkiksi Harrisin pisteiden ympäriltä pieni pikseliympäristö ihan harmaasävykuvana, tai vaihtoehtoisesti harmaasävyhistogrammi. Myös itse Harrisin funktion arvo kuvailee pistettä jollakin tavalla, samoin rakennetensorin tai Hessen matriisin ominaisarvot. Nykyään kuitenkin tyypillisesti muodostetaan erilaisia gradienttihistogrammeja pisteen ympäristöstä.

SIFT

Kaksi erittäin suosittua pistepiirteiden etsintämenetelmää ovat SURF ja SIFT. Ne ovat melko monimutkaisia algoritmeja, jotka esitellään nyt lyhyesti.

SIFT eli scale-invariant feature transform on eräs suosituimmista pistepiirteiden hakumenetelmistä. Se sisältää menetelmä sekä hyvin pisteiden löytämiseen useissa skaaloissa että pisteiden kuvailuun deskriptorin avulla.

Algoritmin vaiheet pääpiirteissään ovat

• kuvan konvolvointi eri kokoisilla gaussisilla maskeilla,
• vierekkäisten konvolvoitujen kuvien erotus lasketaan jolloin saadaan DoG,
• valitaan pisteet jotka ovat lokaaleja maksimeja sekä kuva-avaruudessa että skaala-avaruudessa, eli verrataan pikseliä naapureihinsa ja vastaavaan 9 pikselin naapurustoon naapuriskaaloissa,
• interpoloidaan näiden kandidaattipisteiden sijainti pikseliä paremmalla tarkkuudella,
• hylätään kandidaattipisteet joilla on huono kontrasti,
• hylätää reunapikselit Hessen matriisin avulla.

Jokaiselle valitulla pisteelle lasketaan pääasiallinen suunta laskemalla gradientin magnitudi ja suunta pisteen ympäristössä ja tekemällä näistä suuntahistogrammi. Pisteen pääasiallinen suunta on se suunta, joka esiintyy useimmin histogrammissa. Jos on myös muita suuntia, jotka esiintyvät lähes yhtä monta kertaa (alkuperäisessä algoritmissa 80% pääasiallisen suunnan esiintymiskerroista), jokaiselle suunnalle luodaan oma piste, jolle lasketaan deskriptori.

Deskriptori lasketaan pisteen dominoivan suunnan mukaisesti. Pisteen ympäriltä muodostetaan 16x16-kokonen ympäristö, jonka sisältä lasketaan 4x4 uutta suuntahistogrammia, joista jokaisessa on 8 lokeroa. Lopulta siis saadaan vektori, jossa on 4x4x8 eli 128 elementtiä. Tämä vektori normalisoidaan yksikkövektoriksi.

Tämän selostuksen perusteella lienee selvää, että SIFT-menetelmän suurin puute on vaadittava laskentateho. Sekä pisteiden etsiminen, deskriptorin luominen että deskriptorien etsiminen ja vertaileminen ovat melko raskaita operaatioita. Menetelmä kuitenkin toimii melko hyvin. Löwen alkuperäinen SIFT-paperi on yksi niistä papereista, jotka kannattaa lukea jos aihe yhtään kiinnostaa.

SURF

SURF eli speeded up robust features on nopeampi kuin SIFT, ja myös erittäin suosittu menetelmä. Sekin sisältää menetelmän sekä pisteiden löytämiseksi että niiden kuvailemiseksi, ja SURF-deskriptoreja käytetään toisinaan myös toisilla menetelmillä löydettyjen pisteiden kuvailemiseen.

SURF-menetelmän nopeus saavutetaan käyttämällä laatikkofilttereitä integraalikuvien kanssa. Siinä approksimoidaan toisen asteen derivaattoja laskemalla. Algoritmin vaiheet pääpiirteissään ovat

• Hessen matriisin laskeminen useissa skaaloissa approksimoiden toisen asteen derivaattoja eri kokoisten laatikkofilttereiden avulla,
• matriisin determinanttien lokaalien maksimien laskeminen,
• maksimipisteiden sijainnin interpolointi sekä kuvassa että skaalassa.

SURF-deskriptorit ovat Haarin wavelet-funktioiden histogrammeja, ja myös näiden wavelet-funktioiden laskemisessa käytetään laatikoita ja integraalikuvia. Myös tämä histogrammin normalisoidaan Haar-wavelettien pääasiallisen suunnan mukaan. Jos suunnalla ei ole merkitystä, normalisointi voidaan jättää pois. Varsinaisessa deskriptorissa käytetään myös 4x4:ää aluetta valitun pisteen ympärillä, tarvittaessa normalisoituna pääasiallisen suunnan mukaan. Jokaisesta pienemmästä laatikosta lasketaan Haarin wavelet-funktioiden summa 5x5 pisteestä ja näistä vasteista lasketaan x- ja y-koordinaattien summa ja summan itseisarvo. Nämä arvot ovat varsinaisen deskriptorin arvot, eli saadaa 4x4x4 eli 64 elementtiä.

Nämä kaksi esimerkkiä osoittanevat hyvin, mitkä ovat pääasialliset periaatteet pistepiirteiden etsinnässä ja kuvailussa.

Bonus: Gabor-filtterit

Gaussin funktion korkeampien derivaattojen lisäksi toinen suosittu tapa reunojen ja tekstuurien kuvailuun ovat Gabor-filtterit. Gaussin funktion derivaatat ovat periaatteessa Gaussin funktioita kerrottuna Hermiten polynomeilla, ja Gaussin eksponenttifunktio pakottaa ne pysymään kellokäyrän alla. Samaan tapaan Gabor-funktiossa kerrotaan Gaussin funktiota harmonisella funktiolla, joka tässä tapauksessa on kosini. Muuttamalla kosinin aallonpituutta ja vaihetta sekä kääntämällä kosinin aaltotasoa saadaan monia erilaisia kapeisiin reunoihin ja toistuviin kuvioihin reagoivia filttereitä. Itse asiassa Gaborin funktiot ovat hyvin lähellä korkean asteen Gaussin derivaattoja.

Mallikoodi gabor-filtterien muodostamiseksi löytyy kurssireposta: ilman_graphicstoolsia/Gabor.hs. Näitä voi käyttää esimerkiksi ensi tutoriaalin segmentointimenetelmien kanssa, jolloin alla olevan kuvan heinäsuova pitäisi pystyä segmentoimaan erilleen:

Tehtävä

Etsi kaikki tämän kuvan

kaltaiset neulat seuraavasta kuvasta:

hyödyntäen opittuja taitoja. Vinkkejä:

• Etsi mallikuvasta selkeästi erottuvia kohteita joko Harrisin pisteiden tai Hessen determinantin tai jonkin muun funktion avulla.
• Kuvaile löydettyjä pisteitä jonkin sopivan funktion avulla, esimerkiksi momenttimatriisin, Harrisin funktion, Hessen matriisin, jomman kumman matriisin ominaisarvojen tms. avulla.
• Etsi kohdekuvasta pisteitä samaan tapaan ja vertaile niistä laskettuja funktion arvoja mallikuvan pisteiden kanssa.

Mallikoodia löytyy kansiosta ilman_graphicstoolsia/Harris.hs.