Aihe
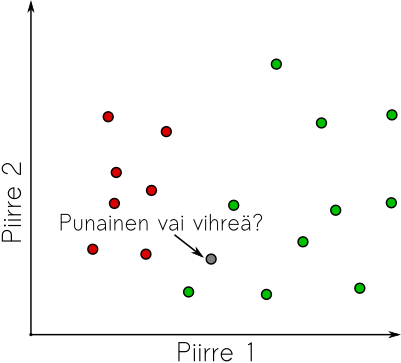
Jatketaan piirreavaruuksien kanssa touhuamista. Tällä kertaa pyrimme ratkaisemaan kysymystä “kuuluuko piirrepiste X mihin annetuista joukoista Y_i”. Toisinsanoen, jos meillä on vaikkapa kuvasarjat muttereista ja ruuveista niin aiomme määritellä algoritmeja, jotka kertovat kumpi esineistä on seuraavassa kuvassa. Tätä kutsutaan luokitteluksi.
Käsite on piirreavaruuden kannalta muotoiltuna hyvin laaja. Voimme luokitella kuvapisteet tai niiden pienet ympäristöt “taustaksi” ja “kohteeksi” eli erottaa kuvasta vaikkapa kasvot tai rekisterikilvet. Lisäksi pystymme erottamaan kohteet toisistaan: “kuvassa on Matti” tai “kuvassa on mutteri”.
Peruslähtökohta luokittelutehtävien ratkaisuun koostuu seuraavista vaiheista:
- Näytteiden hankinta
- Näytejoukon jakaminen koulutus- ja testijoukoiksi
- Piirrevektoreiden irroittaminen (Ts. näytteiden kuvaus piirreavaruuteen)
- Piirrevektoreiden skaalaaminen/esikäsittely koulutusjoukon pohjalta
- Luokitinmenetelmän parametrien kalibrointi
- Luokittimen ‘koulutus’
- Testaus koulutusjoukolla.
Tässä tutoriaalissa esittelemme olennaiset menetelmät esimerkein ja jätämme lukijan tehtäväksi kokonaisen ketjun muodostamisen.
Alustavat toimenpiteet
Ennen kuin voimme lähteä ratkaisemaan luokittelutehtävää, meidän täytyy hankkia riittävä määrä aineistoa, joka kattaa mahdollisimman laajasti tunnistettavat kohteet, sillä koneoppimisen ongelmiin kuuluu usein se, että niiden yleistyskyky on ihmiseen verrattuna alkeellinen ja esimerkiksi kuvien tapauksessa pelkkä ennenäkemätön valaistusolosuhde voi estää luokittimen toiminnan.
Lisäksi on ehdottoman tärkeää erottaa koulutusaineistosta testiaineisto, sillä tarvitsemme jonkun keinon tarkastaa, että luokittimemme pystyy yleistämään. Esimerkiksi, jos yritämme oppia tunnistamaan kuvasta koiran viiden esimerkkikuvan perusteella on helppo luoda luokitusmenetelmä, joka tunnistaa aina ehdottomasti alkuperäiset viisi esimerkkiä, mutta ei koskaan mitään muuta.
Näytejoukon keräämisen jälkeen kuvaamme kohteet mielestämme asianmukaiseen piirreavaruuteen ja alamme pohtia luokittelua.
Piirrevektoreiden esikäsittely ja pääkomponenttianalyysi
Tämä teksti pohjautuu artikkeliin Eigenfaces for recognition
Kuten aiemmissa tutoriaaleissa olemme huomanneet, piirreavaruutemme koostuvat usein pisteistä, joiden välillä ei ole yleispätevästi määriteltävää metriikkaa. On esimerkiksi varsin tapauskohtaista päättää kuinka kaukana pisteet (1 metri, vaalean vihreä) ja (1.2 metriä, sininen) ovat toisistaan. Kuitenkin, kaikki luokitinmenetelmät toimivat nimeomaan metriikan perusteella, joten meidän on pakko valita jokin metrinen piirreavaruus.
Jos käyttäisimme yksinkertaisia piirteitä, kuten kohteen pituus, leveys ja väri, voisimme luultavasti määritellä tapauskohtaisesti jonkin tehtävään sopivan skaalauksen muuttujien arvoille. Kuitenkin, jos piirreavaruudemme on monimutkainen ja moniulotteinen, emme tähän pysty. Tarkastellaan esimerkkinä perinteistä naiivia kasvojentunnistusongelmaa, jossa pyrimme tunnistamaan onko seuraavan henkilö
tässä kuvagalleriassa:
käyttäen piirrevektorina kuvan kaikkia pikseleitä. Ts. piirrevektorimme koostuu kuvan kuvapisteiden harmaasävyarvoista lueteltuna järjestyksessä vasemmasta yläkulmasta oikeaan alakulmaan.
\(F_{kuva}(I) = \left\{ \left[\begin{array}{c} I(x,y)\end{array}\right] \bigg| (x,y) \in \text{dom}(I) \right\}\),
Tällöin esimerkiksi jokainen \(100\times 100\)-kokoinen kuva muodostaa 10 000 elementtiä pitkän piirrevektorin ja hyvin hankalan luokittelutehtävän. Metriikka-ajattelun kannalta voisimme toki toivoa, että jos laskemme tälläisten vektoreiden etäisyydet toisistaan niin samankaltaisten ihmisten kuvat olisivat lähellä toisiaan. Valitettavasti vain näin ei ole. Vektorit eivät kuvaa mitään järjellistä ominaisuutta kuvassa.
Seuraavaksi havaitsemme sen, että kasvokuvat ovat pieni osajoukko kaikista mahdollisista kuvista. Näinollen voisi toivoa, että ne virittäisivät oman, yksinkertaisemman aliavaruuden, jossa tunnistustehtävä helpottuisi. Herää kysymys, olisiko mahdollista keksiä sellainen kanta, jossa kuvat olisi helpompi erottaa toisistaan?
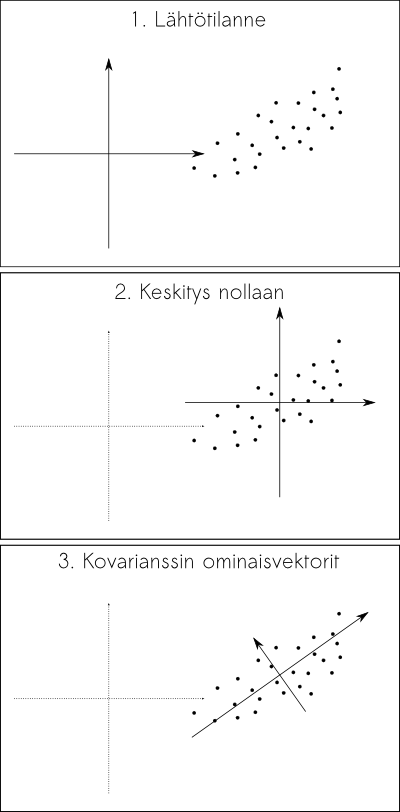
Fourier-muunnoksella voisimme tarkastella taajuuskomponentteja, mutta ihmisten erottaminen toisistaan sen perusteella, että toisen kuvassa on enemmän korkeataajuuskomponentteja ei kuullosta kovin lupaavalta. Sen sijaan voimme käyttää erästä 1900-luvun alussa keksittyä menetelmää, eli pääkomponenttianalyysiä, joka pyrkii esittämään datajoukon sellaisessa koordinaatistossa, jossa se on mahdollisimman korreloimaton, tai toisinsanoen, avaruudessa minkä kantavektorit mukailevat dataa mahdollisimman hyvin:
Pääkomponenttianalyysillä voidaan myös selvittää kuinka paljon datajoukon vaihtelusta selittyy kunkin kantavektorin mukaan, eli jos datamme on kovin moniulotteista, mutta se koostuu hyvin samankaltaisista näytteistä, kuten vaikkapa kasvokuvista, voimme valita tunnistamista varten ne kantavektorit, jotka selittävät eniten datan rakenteesta.
Menetelmän idea selviää yo. kuvasta:
- Lasketaan piirrevektoreiden \(V_i\) keskiarvo \(M\)
- Lasketaan piirrevektoreiden sijainnit \(M\) keskeisessä koordinaatistossa \(C_i=V_i-M\)
- Lasketaan pisteiden \(C_i\) kovarianssimatriisi \(\Sigma\) \(\Sigma=\frac{1}{n} C C^T\). Kovarianssimatriisi kertoo datajoukon pisteiden vaihtelun ja yhteisvaihtelun määrän.
Laske kovarianssimatriisin ominaisvektorit ja ominaisarvot. Ominaisvektorit muodostavat uuden kannan ja ominaisarvot kertovat datan vaihtelun kyseisen vektorin suuntaan. (Idea: Kovarianssimatriisi kuvaa yksikköpallon ellipsiksi datan ympärille ja ominaisarvot antavat ellipsin puoliakselit. Testaa kynällä ja paperilla)
Koska kuvavektorin pituus saattaa olla hyvin suuri, niin huomataan, että sen ominaisvektorit voidaan laskea helpomminkin. Jos \(v_i\) on matriisin \(C^T C\) ominaisvektori, niin \(C^T C v_i = s v_i\). Kertomalla \(C\):llä vasemmalta, saamme \(C C^T (C v_i) = s (C v_i)\) ja näinollen huomaamme, että \(C v_i\) on \(C C^T\):n ominaisvektori. Koska \(C^T C\) matriisissa on vain näytteiden määrän neliön verran alkioita, eikä suinkaan kuvan pikseleiden neliön verran, tämä on huomattavasti kevyempi laskutoimitus.
Jos sovellamme tätä menettelyä kasvogalleriaamme, saamme seuraavat kantavektorit, jotka ovat takaisin kuvaksi muutettuina seuraavan näköiset.
Tuttuun tapaan, voimme nyt projisoida kuvasta \(i\) muodostetun piirrevektorin \(V_i\) pääkomponenttien muodostamaan kantaan \(P_n(v_i)=<v_i|e_n>\) (missä \(e_n\) merkitsee \(n\):ttä pääkomponenttia.) Tämä on operaation kustannus on lineaarinen kuvan koon suhteen, eli menetelmä on hyvin nopea sen jälkeen kun pääkomponentit ovat löytyneet.
Lyhyenä haittapuolena kerrottakoon, että luokitustehtävissä olennainen informaatio ei aina ole suinkaan suurimman varianssin selittävänä akselina. (Ks. seuraava tehtävä g).
Tehtävä
- Laske muutamalle kasvokuvalle niiden etäisyys toisistaan käyttäen suoraa kuvausta piirreavaruuteen.
- Millaiset asiat kuvissa näyttäisivät vaikuttavan eniten?
- Laske muutamalle kasvokuvalle etäisyys pääkomponenttien määräämässä piirreavaruudessa. Millaiset asiat vaikuttavat nyt?
- Entäpä jos käytät vain “voimakkaimpia” pääkomponentteja.
- Pystytkö löytämään esimerkkikasvot annetusta kuvakokoelmasta pelkästään vertaamalla kasvojen etäisyyksiä keskenään? (Ks. Kurssisivun repo/ilman_graphicstoolsia.)
- Spekuloi mitä tapahtuisi jos kuvissa olisi erilainen valaistus? Voisiko sen korjata?
- Entäpä jos ihmisillä on kovin erilaisia ilmeitä? Mitä silloin tapahtuisi? (Ts. miksi passikuvassa ei saa hymyillä.)
Yksinkertaisin luokitin: K-lähintä naapuria
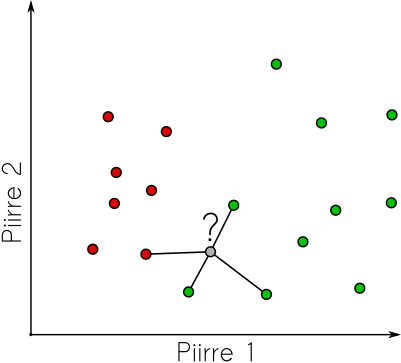
Edellisessä tehtävässä tunnistimme kasvot valitsemalla tunnettujen kasvojen joukosta ne kasvot, jotka olivat piirreavaruudessa lähimpänä etsimäämme. Tämä naiivi strategia on kuitenkin äärimmäisen tehokas luokittelumenetelmä jo sinänsä. Ongelma sen kanssa on lähinnä se, että epäselvissä tapauksissa tulos on arpapeliä. Jos oletamme, että aineistomme olisi kerätty fiksusti ja samasta kohteesta tai henkilöstä olisi useampia eri ilmein varustettuja kasvokuvia voimme laajentaa tunnistusmenetelmäämme hieman vakaampaan suuntaan: Valitaan tunnistettavalle pisteelle K-kappaletta lähimpiä pisteitä piirreavaruudesta ja päätellään kohteen luokka (tai henkilön nimi) vaikkapa sen mukaan, minkä luokan tai henkilön edustajia lähimpien pisteiden joukossa on eniten.
Lisäksi voimme käyttää lähimpiä naapureita arviona sille, kuinka luotettavasti kohde on tunnistettu. Jos lähimmässä naapurustossa ei ole selvää enemmistöä, tunnistustulos on tietysti epävarma.
Koska tässä menetelmässä on jo yksi parametri, se täytyy asettaa myöskin tehtävän mukaiseksi. Jos piirrepisteet ovat selkeästi erillään, pieni K-arvo lienee hyvä valinta ja jos datajoukossa on paljon päällekäisyyttä ja epävarmuutta niin suuri K voisi olla parempi. Kuitenkin, tämä on hyvä testata käyttäen koulutusjoukkoa.
Tehtävä
- Etsi parempi luokitin. Selvitä itsellesi yleisellä tasolla, mitä ovat neuroverkot, tukivektorikoneet ja päätöspuut. Sitten mene ja käy tiedonlouhinta tai vastaava kurssi.