Ohjaus 1: Tuuliresurssien karakterisointi
Ohjauksessa harjannutaan tuulitietojen tarkasteluun MATLABia apuna käyttäen. Aineistoa käytetään Kemian laitoksen katolla sijaitsevalla Davis Weather -sääasemalla vuonna 2007 tehtyjä havaintoja erityisesti tuulen nopeudesta ja suunnasta.
Harjoituksessa käytettävä aineisto on ladattavissa os. otos07.mat
Harjoituksen aluksi:
- Luo työasemalle hakemisto c:\MyTemp\FYSS481\ohjaus1 ja kopio havaintoaineisto tähän hakemistoon.
- Käynnistä MATLAB napsauttamalla Start -painiketta. Kirjoita hakuruutuun MATLAB ja valitse sitten tulosluettelosta MATLAB R2013a.
- MATLAB in käynnistyttä siirry luomaasi työhakemistoon antamalla Command Window ikkunassa komento cd c:\MyTemp\FYSS481\ohjaus1.
- Siirry suorittamaan annettuja tehtäviä. Ohjauksen aikana suoritettavat tehtävät on kirjoitettu harmaalle alustalle ja ne suoritetaan Command Window ikkunassa.
Contents
Tuulitietojen esittäminen aikasarjana
Tietyllä korkeudella suoritetut tuulimittaukset on tallennettu taulukkoon:
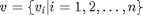
load otos07; % Ladataan tuulitiedot v = WindSpeed; % Kopioidaan tuulen nopeushavainnot uuteen taulukkoon d = WindDir; % Kopioidaan tuulen suuntahavainnot uuteen taulukkoon n = size(v) % Otoskoko tuulen nopeushavainnoista
n =
452055 1
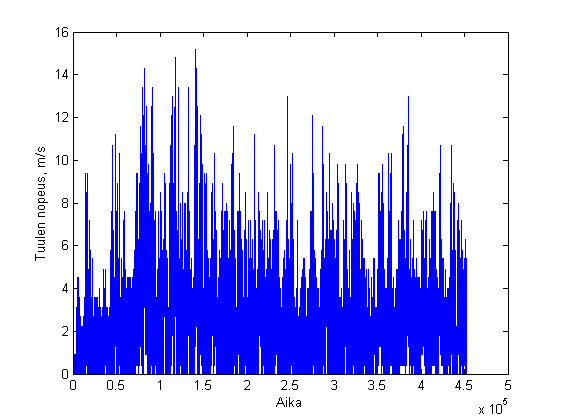
Piirretään kuvaaja tuulen nopeushavaintojen aikasarjasta:
plot(v,'-') xlabel('Aika') ylabel('Tuulen nopeus, m/s')
Kategoristen muuttujien frekvenssijakauma: Tuulen suunta
Oletetaan aluksi, että muuttuja 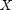 on luokka-asteikon muuttuja. Olkoot sen mahdooliset arvot eli luokituksessa käytettvät luokat
on luokka-asteikon muuttuja. Olkoot sen mahdooliset arvot eli luokituksessa käytettvät luokat 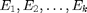 . Luokan
. Luokan 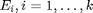 frekvenssi on luku, joka ilmoittaa, kuinka monta kertaa arvo
frekvenssi on luku, joka ilmoittaa, kuinka monta kertaa arvo 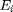 esiintyy aineistossa. Tälle frekvenssille käytetään merkintää
esiintyy aineistossa. Tälle frekvenssille käytetään merkintää 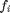 . Muuttujan
. Muuttujan 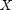 frekvenssijakauma kertoo kaikkien luokkien frekvenssit. Luokan
frekvenssijakauma kertoo kaikkien luokkien frekvenssit. Luokan 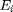 suhteellinen frekvenssi on luku
suhteellinen frekvenssi on luku 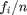 . Nämä luvut muodostavat suhteellisen frekvenssijakauman.
. Nämä luvut muodostavat suhteellisen frekvenssijakauman.
Taulukkoon d on tallennettu havaintoaineisto tuulen suunnasta tarkasteluvälillä. Tuulen suunta ilmoitetaan ilmansuuntana, josta tuuli tulee. Tuulen suunta havaintojen luokitteluun on käytetty 17 luokkaa 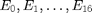 . Luokka
. Luokka 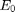 on varattu havainnoille, kun ilma on tyyni. Luokat
on varattu havainnoille, kun ilma on tyyni. Luokat 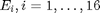 ovat vastaavasti sektorit N, NNE, NE, \ldots, NW, NNW niiden luonnollisessa järjestyksessä ilman suunnan mukaan.
ovat vastaavasti sektorit N, NNE, NE, \ldots, NW, NNW niiden luonnollisessa järjestyksessä ilman suunnan mukaan.
Määritellään luokkien arvot taulukkoon E ja piirretään tuulen suunnan frekvenssijakauma MATLABin hist funktiolla.
E = 0:16 hist(d,E) title('Tuulen suunta') xlabel('Luokka') ylabel('Frekvenssi')
E =
Columns 1 through 13
0 1 2 3 4 5 6 7 8 9 10 11 12
Columns 14 through 17
13 14 15 16
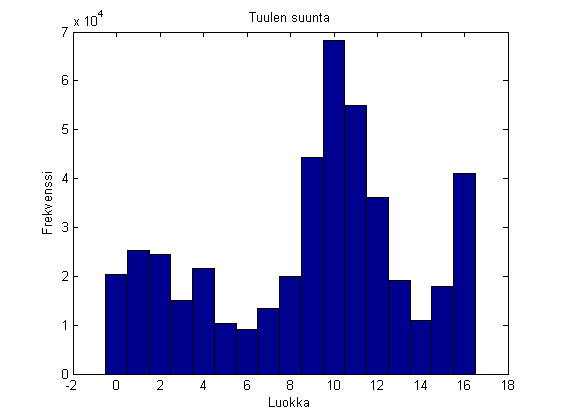
Määritellään ensin luokkien 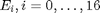 suhteelliset frekvenssit hist funktiolla ja tallennetaan frekvenssit taulukkoon
suhteelliset frekvenssit hist funktiolla ja tallennetaan frekvenssit taulukkoon 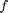 . Tämän jälkeen voimme laskea luokkien suhteelliset frekvenssit
. Tämän jälkeen voimme laskea luokkien suhteelliset frekvenssit 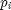 jakamalla frekvenssit niiden summalla
jakamalla frekvenssit niiden summalla 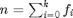 .
.
f = hist(d,E) n = sum(f) p = f./n
f =
Columns 1 through 6
20284 25199 24409 15132 21692 10330
Columns 7 through 12
9127 13460 19860 44263 68254 54863
Columns 13 through 17
36191 19086 10996 17955 40954
n =
452055
p =
Columns 1 through 7
0.0449 0.0557 0.0540 0.0335 0.0480 0.0229 0.0202
Columns 8 through 14
0.0298 0.0439 0.0979 0.1510 0.1214 0.0801 0.0422
Columns 15 through 17
0.0243 0.0397 0.0906
Suhteellisen frekvenssijakauman graafinen esitys saadaan MATLABin bar funktiolla:
bar(E,p) title('Tuulen suunta') xlabel('Luokka') ylabel('Suhteellinen frekvenssi')
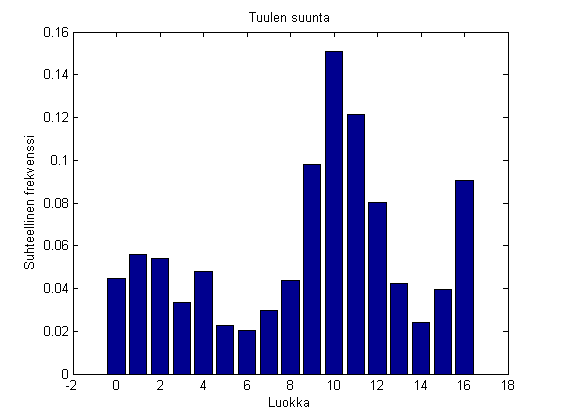
Prosenttinen frekvenssijakauma saadaan, kun suhteelliset frekvenssit ilmaistaan prosentteina niiden summasta  .
.
bar(E,100*p) title('Tuulen suunta') xlabel('Luokka') ylabel('Prosenttinen frekvenssi, %')
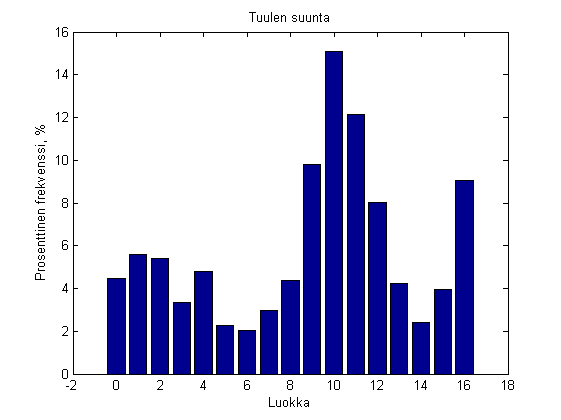
Numeeristen muuttujien frekvenssijakauma: Tuulen nopeus
Jos muuttujalla on paljon mahdollisia arvoja suhteessa havaintojen lukumäärään, jäävät frekvenssit pieniksi ja tällöin aineisto on luokiteltava.
Oletetaan, että aineisto halutaan luokitella  luokkaan. Tällöin valitaan aluksi reaaliluvut
luokkaan. Tällöin valitaan aluksi reaaliluvut 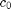 ja
ja 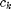 siten ,että väli
siten ,että väli ![$[c_0,c_k]$](karakterisointi_eq94337.png) sisältää kaikki luokiteltavan muuttujan
sisältää kaikki luokiteltavan muuttujan 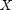 havaitut arvot. Tämä väli jaetaan
havaitut arvot. Tämä väli jaetaan  osaväliin
osaväliin ![$[c_0,c_1],[c_1,c_2],\ldots,[c_{k-1},c_k]$](karakterisointi_eq94668.png) . Merkitään
. Merkitään ![$I_i = [c_{i-1},c_i]$](karakterisointi_eq71566.png) . Luokan
. Luokan 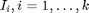 frekvenssi on niiden havaintoaineistossa olevien havaintojen lukumäärä, joilla muuttujan
frekvenssi on niiden havaintoaineistossa olevien havaintojen lukumäärä, joilla muuttujan 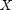 arvo on välillä
arvo on välillä 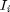 . Muuttujan
. Muuttujan 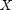 frekvenssijakaumailmaisee kaikkien luokkien
frekvenssijakaumailmaisee kaikkien luokkien 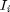 fekvenssit.
fekvenssit.
Tarkastellaan taulukkoon  kerättyjä tuulen nopeuksia. Koska tuulen nopeuden pienin arvo on aina 0, asetetaan
kerättyjä tuulen nopeuksia. Koska tuulen nopeuden pienin arvo on aina 0, asetetaan 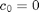 . Etsitään suurin
. Etsitään suurin  :n arvo havaintoaineistosta MATLABin max funktiolla ja pyöristetään löytynyt arvo ylöspäin lähimpään kokonaislukuun.
:n arvo havaintoaineistosta MATLABin max funktiolla ja pyöristetään löytynyt arvo ylöspäin lähimpään kokonaislukuun.
c0 = 0.0 % Asetetaan c_0 = 0 ck = max(v) % Etsitään v:n suurin arvo ck = ceil(ck) % Pyöristetään ck:n arvo ylöspäin lähimpään kokonaislukuun
c0 =
0
ck =
15.2000
ck =
16
Valitaan osavälien lukumäärä  ja muodostetaan taulukko luokista
ja muodostetaan taulukko luokista 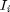 keskimmäiset arvot. Valitaan
keskimmäiset arvot. Valitaan  siten, että osavälien pituus on aluksi l = 0,5 m/s käyttäen yhtälöä
siten, että osavälien pituus on aluksi l = 0,5 m/s käyttäen yhtälöä
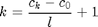
l = 0.25 k = (ck - c0)/l + 1 I = linspace(c0,ck,k)
l =
0.2500
k =
65
I =
Columns 1 through 7
0 0.2500 0.5000 0.7500 1.0000 1.2500 1.5000
Columns 8 through 14
1.7500 2.0000 2.2500 2.5000 2.7500 3.0000 3.2500
Columns 15 through 21
3.5000 3.7500 4.0000 4.2500 4.5000 4.7500 5.0000
Columns 22 through 28
5.2500 5.5000 5.7500 6.0000 6.2500 6.5000 6.7500
Columns 29 through 35
7.0000 7.2500 7.5000 7.7500 8.0000 8.2500 8.5000
Columns 36 through 42
8.7500 9.0000 9.2500 9.5000 9.7500 10.0000 10.2500
Columns 43 through 49
10.5000 10.7500 11.0000 11.2500 11.5000 11.7500 12.0000
Columns 50 through 56
12.2500 12.5000 12.7500 13.0000 13.2500 13.5000 13.7500
Columns 57 through 63
14.0000 14.2500 14.5000 14.7500 15.0000 15.2500 15.5000
Columns 64 through 65
15.7500 16.0000
Nyt voimme luokitella taulukossa v olevat havainnot luokkiin 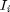 ja määritettyä muuttujan
ja määritettyä muuttujan  fekvenssijakauman käyttäen MATLABin hist funktiota. Lasketaan myöskin suhteellinen frekvenssijakauma.
fekvenssijakauman käyttäen MATLABin hist funktiota. Lasketaan myöskin suhteellinen frekvenssijakauma.
f = hist(v,I) % Tuulen nopeuden frekvenssit n = sum(f) % Havaintojen lukumäärä p = f./n % Tuulen nopeuden suhteelliset frekvenssit
f =
Columns 1 through 6
50230 0 56174 0 43596 36827
Columns 7 through 12
0 39492 0 42531 0 39423
Columns 13 through 18
33539 0 27453 0 21876 0
Columns 19 through 24
16670 0 12277 0 8812 6238
Columns 25 through 30
0 4389 0 3279 0 2399
Columns 31 through 36
1723 0 1371 0 1036 0
Columns 37 through 42
808 0 568 418 0 313
Columns 43 through 48
0 197 0 156 103 0
Columns 49 through 54
66 0 35 0 23 0
Columns 55 through 60
23 0 2 5 0 2
Columns 61 through 65
0 1 0 0 0
n =
452055
p =
Columns 1 through 7
0.1111 0 0.1243 0 0.0964 0.0815 0
Columns 8 through 14
0.0874 0 0.0941 0 0.0872 0.0742 0
Columns 15 through 21
0.0607 0 0.0484 0 0.0369 0 0.0272
Columns 22 through 28
0 0.0195 0.0138 0 0.0097 0 0.0073
Columns 29 through 35
0 0.0053 0.0038 0 0.0030 0 0.0023
Columns 36 through 42
0 0.0018 0 0.0013 0.0009 0 0.0007
Columns 43 through 49
0 0.0004 0 0.0003 0.0002 0 0.0001
Columns 50 through 56
0 0.0001 0 0.0001 0 0.0001 0
Columns 57 through 63
0.0000 0.0000 0 0.0000 0 0.0000 0
Columns 64 through 65
0 0
Piirretään tuulen nopeuden frekvenssijakauman ja suhteellisen frekvenssijakauman kuvaajat.
bar(I,f) title('Tuulen nopeus') xlabel('Tuulen nopeus, m/s') ylabel('Frekvenssi') bar(I,f) title('Tuulen nopeus') xlabel('Tuulen nopeus, m/s') ylabel('Suhteellinen frekvenssi')
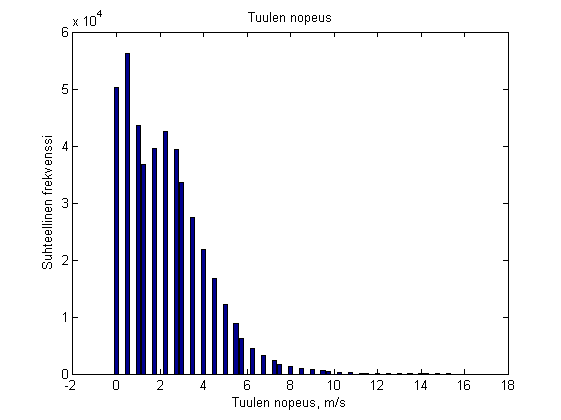
Muuttujan 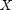 summafrekvenssit
summafrekvenssit 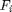 määritellään asettamalla
määritellään asettamalla
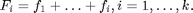
Summafrekvenssi 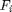 kertoo, kuinka monella populaatioyksiköllä havaintoaineistossa muuttujan
kertoo, kuinka monella populaatioyksiköllä havaintoaineistossa muuttujan 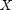 arvo on pienempi tai yhtäsuuri kuin
arvo on pienempi tai yhtäsuuri kuin 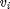 . Summajakaumassa (engl. cumulative frequency distribution) kerrotaan muuttujan eri arvoihin liittyvät summafrekvenssit. Suhteellista summafrekvenssijakaumaa kutsutaan myös otoskertymäfunktioksi.
. Summajakaumassa (engl. cumulative frequency distribution) kerrotaan muuttujan eri arvoihin liittyvät summafrekvenssit. Suhteellista summafrekvenssijakaumaa kutsutaan myös otoskertymäfunktioksi.
F = zeros(1,k); % Alustetaan summafrekvenssien taulukko for i=1:k % Määritetään summafrekvenssien arvot if i==1 F(i) = f(i); else F(i) = F(i - 1) + f(i); end end
Piirretään summafrekvenssijakauman summakäyrä:
plot(I+0.5*l,F) title('Tuulen nopeus') xlabel('Tuulen nopeus, m/s') ylabel('Summafrekvenssi')
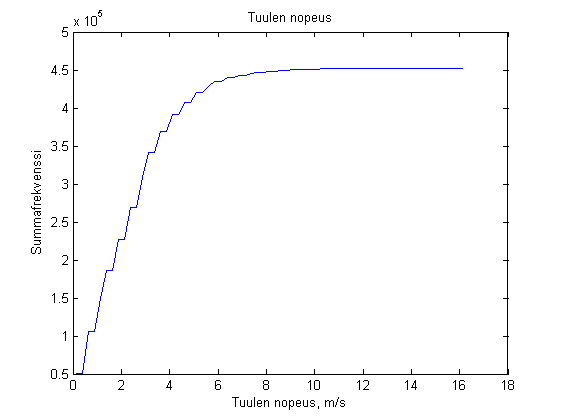
Muuttujan 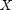 suhteellinen summafrekvenssit
suhteellinen summafrekvenssit 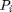 määritellään asettamalla
määritellään asettamalla
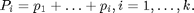
P = zeros(1,k); % Alustetaan suhteellisten summafrekvenssien taulukko for i=1:k % Määritetään suhteellisten summafrekvenssien arvot if i==1 P(i) = p(i); else P(i) = P(i - 1) + p(i); end end
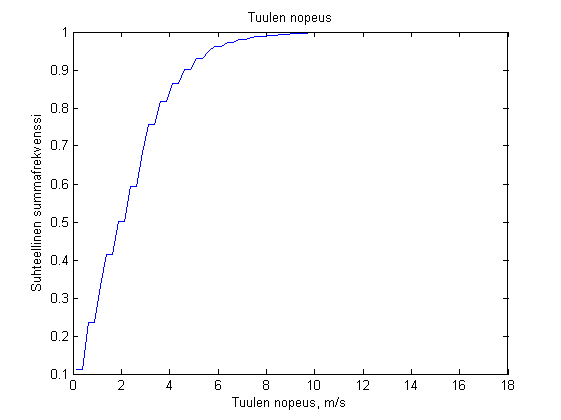
Piirretään suhteellisen summafrekvenssijakauman summakäyrä
plot(I+0.5*l,P) title('Tuulen nopeus') xlabel('Tuulen nopeus, m/s') ylabel('Suhteellinen summafrekvenssi')
Otoksen jakauman tunnusluvut: Keskiluvut
Fekvenssijakaumaan sisältyvä informaatio voidaan taulukoinnin ja kuvallisen esityksen lisäksi tiivistää yhteen ja useampaan tunnuslukuun (engl. statistics).
Jakauman sijainnin tunnuslukuja:
- Moodi (engl. mode) on se muuttujan arvo, jonka frekvenssi jakaumassa on suurin. Muuttujan
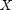 moodille käytetään merkintää
moodille käytetään merkintää 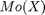 tai pelkästään
tai pelkästään 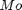 . Moodi on suomeksi tyyppiarvo.
. Moodi on suomeksi tyyppiarvo. - Mediaani (engl. median) vaatii vähintää järjestettävän mittauksen. Muuttujan
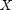 mediaani,
mediaani, 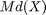 tai vain
tai vain 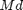 , on se muuttujan arvo tai luokka, jonka alapuolella (mediaani mukaanlukien) jää ainakin puolet havaintoarvoista ja yläpuolelle (mediaani mukaanlukien) samin ainakin puolet havaintoarvoista.
, on se muuttujan arvo tai luokka, jonka alapuolella (mediaani mukaanlukien) jää ainakin puolet havaintoarvoista ja yläpuolelle (mediaani mukaanlukien) samin ainakin puolet havaintoarvoista. - Keskiarvot: Jos muuttujan
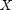 havainnot ovat
havainnot ovat 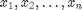 on näiden havaintojen (aritmeettinen) keskiarvo (engl. arithmetic mean)
on näiden havaintojen (aritmeettinen) keskiarvo (engl. arithmetic mean)
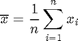 $.
$.
v_Mo = mode(v) % Otoksen moodi v_Md = median(v) % Otoksen mediaani v_Mu = mean(v) % Otoksen aritmeettinen keskiarvo
v_Mo =
0.4000
v_Md =
1.8000
v_Mu =
2.2488
Otoksen jakauman tunnusluvut: Hajontaluvut
Hajontalukujen avulla kuvataan aineistossa esiintyvän vaihtelun määrää. Niiden avulla voidaan ilmaista, kuinka voimakkaasti mittaustulokset vaihtelevat havaintoyksiköstä toiseen tai missä määrin ne keskittyvät keskiluvun läheisyyteen.
Jakauman vaihtelun tunnuslukuja:
- Keskihajonta (engl. standard deviation) on tärkein sovelluksissa käytetty hajontaluku. Keskihajonnan neliötä kutsutaan varianssiksi (engl. variance). Keskihajonnan ja varianssin laskemiseen käytetään eri kaavoja riippuen siitä, onko kyseessä koko populaatio vai otos.
- Variaatiokerroin (engl. coefficient of variation) kerrotaan sadalla, jolloin saatu luku kertoo montako prosenttia keskihajonta on otoksen keskiarvosta. Sen avulla voidaan vertailla erilaisten jakaumien keskittymistä.
- Vinous (engl. skewness) on jakauman symmetrian mitta.
sigma = std(v,1) % Koko populaation keskihajonta s = std(v,0) % Otoksen keskihajonta CV = 100.0*(s/v_Mu) % Variaatiokerroin gamma = skewness(v) % Jakauman vinous
sigma =
1.8491
s =
1.8491
CV =
82.2252
gamma =
1.0668
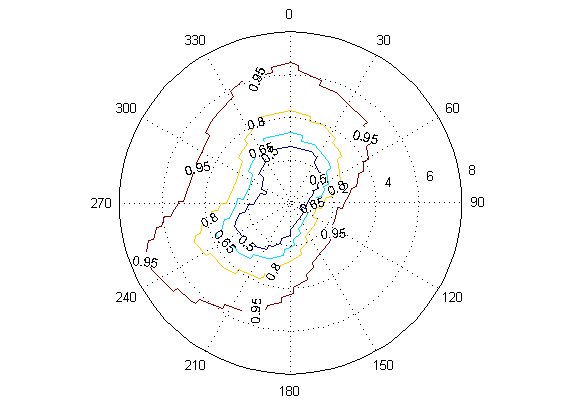
Harjoitus: Tuuliruusu
th = (0:22.5:360)*pi/180; r = I; [TH,R] = meshgrid(th,r); [X,Y] = pol2cart(TH,R); F = zeros(length(I),length(th)); for s = 1:16 idx = find(d == s); fs = hist(v(idx),I); fs = fs./sum(fs); for i=1:k if i==1 Fs(i) = fs(i); else Fs(i) = Fs(i-1) + fs(i); end end F(:,s) = Fs'; end F(:,end) = F(:,1); figure h = polar([0 2*pi],[0 8]); view([90 -90]) delete(h) hold on contour(X,Y,F,[0.5:0.15:1],'ShowText','on') hold off